递归的思想与应用
目录
1、递归的思想
2、递归思想的应用
1、递归求和
2、斐波拉契数列
3、求字符串长度
4、单向链表的转置
5、单向排序链表的合并
6、汉诺塔问题
7、全排列问题
3、递归实现回溯算法
1、回溯的本质
2、逆序打印单链表中的偶数结点
3、八皇后问题
4、小结
1、递归的思想
递归是—种数学上分而自治的思想
-将原问题分解为规模较小的问题进行处理
分解后的问题与原问题的类型完全相同,但规模较小
通过小规模问题的解,能够轻易求得原问题的解
-问题的分解是有限的(递归不能无限进行)
当边界条件不满足时,分解问题(递归继续进行)
当边界条件满足时,直接求解(递归结束)
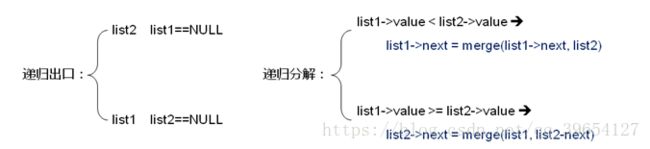
递归模型的一般表示法
递归在程序设计中的应用
-递归函数
函数体中存在自我调用的函数
递归函数必须有递归出口(边界条件)
函数的无限递归将导致程序崩溃
2、递归思想的应用
1、递归求和
求解: Sum(n) = 1 + 2 + 3 + … + n
#include
using namespace std;
unsigned int sum(unsigned int n)
{
if(n > 1)
return n + sum(n - 1);
else
return 1;
}
int main()
{
cout << sum(100) << endl;
return 0;
}
2、斐波拉契数列
-数列自身递归定义: 1, 1, 2, 3, 5, 8, 13, 21, …
#include
using namespace std;
unsigned int fib(unsigned int n)
{
if(n > 2)
return fib(n - 1) + fib(n - 2);
if(n == 1 || n == 2)
return 1;
return 0;
}
int main()
{
for(int i = 1; i < 10; i++)
cout << fib(i) << endl;
return 0;
}
3、求字符串长度
用递归的方法编写函数求字符串长度
#include
using namespace std;
unsigned int _strlen_(const char* s)
{
// if(*s != '\0')
// return 1 + _strlen_(s + 1);
// else
// return 0;
return s ? ( *s ? (1 + _strlen_(s + 1)) : 0 ) : 0;
}
int main()
{
cout << _strlen_("nyist") << endl;
return 0;
}
4、单向链表的转置
出口:空链表的转置为空链表,单链表只有一个结点不需要转置
#include
using namespace std;
struct Node
{
int value;
Node* next;
};
Node* create_list(int v, int len)
{
Node* ret = NULL;
Node* slider = NULL;
for(int i = 0; i < len; i++)
{
Node* n = new Node();
n->value = v++;
n->next = NULL;
if(slider == NULL)
{
slider = n;
ret = n;
}
else
{
slider->next = n;
slider = n;
}
}
return ret;
}
void destory_list(Node* list)
{
while(list)
{
Node* del = list;
list = list->next;
delete del;
}
}
void print_list(Node* list)
{
while(list)
{
cout << list->value << "->";
list = list->next;
}
cout << "NULL" << endl;
}
Node* reserse(Node* list)
{
if(list == NULL || (list->next == NULL)) //空表或单链表只有一个结点
{
return list;
}
else
{
Node* guard = list->next;//标记第1个结点
Node* ret = reserse(list->next);//子表的转置
guard->next = list;//转置后,将标记的结点指向第0个结点
list->next = NULL; //原来首结点的next置NULL
return ret;
}
}
int main()
{
Node* list = create_list(1, 5);
print_list(list);
list = reserse(list);
print_list(list);
destory_list(list);
return 0;
} 5、单向排序链表的合并
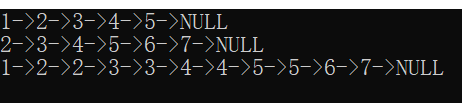
两个有序的单链表合并
#include
using namespace std;
struct Node
{
int value;
Node* next;
};
Node* create_list(int v, int len)
{
Node* ret = NULL;
Node* slider = NULL;
for(int i = 0; i < len; i++)
{
Node* n = new Node();
n->value = v++;
n->next = NULL;
if(slider == NULL)
{
slider = n;
ret = n;
}
else
{
slider->next = n;
slider = n;
}
}
return ret;
}
void destory_list(Node* list)
{
while(list)
{
Node* del = list;
list = list->next;
delete del;
}
}
void print_list(Node* list)
{
while(list)
{
cout << list->value << "->";
list = list->next;
}
cout << "NULL" << endl;
}
Node* merge(Node* list1, Node* list2)
{
if(list1 == NULL)
{
return list2;
}
else if(list2 == NULL)
{
return list1;
}
else if(list1->value < list2->value)
{
// Node* list_ = list1->next;
// Node* list = merge(list_, list2);
// list1->next = list;
// return list1;
return (list1->next = merge(list1->next, list2), list1);
}
else
{
// Node* list2_ = list2->next;
// Node* list = merge(list2_, list1);
// list2->next = list;
// return list2;
return (list2->next = merge(list2->next, list1), list2);
}
}
int main()
{
Node* list1 = create_list(1, 5);
Node* list2 = create_list(2, 6);
print_list(list1);
print_list(list2);
Node* list = merge(list1, list2);
print_list(list);
destory_list(list);
return 0;
} 6、汉诺塔问题
汉诺塔问题
-将木块借助B柱由A柱移动到C柱
-每次只能移动—个木块
- 只能出现小木块在大木块之上
汉诺塔问题分解
-将n-1个木块借助C柱由A柱移动到B柱
-将最底层的唯—木块直接移动到C柱
-将n-1个木块借助A柱由B柱移动到C柱
#include
using namespace std;
void HanoiTower(int n, char a, char b, char c) //a==>scr c==>dest b==>middle
{
if(n == 1)
{
cout << a << "->" << c << endl;
}
else
{
HanoiTower(n-1, a, c, b);
HanoiTower(1, a, b, c);
HanoiTower(n-1, b, a, c);
}
}
int main()
{
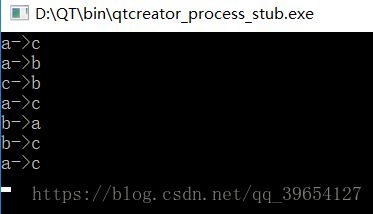
HanoiTower(3, 'a', 'b', 'c');
return 0;
}
7、全排列问题
全排列的递归解法
abc,bac,cba可以看成abc中a与a交换,a与b交换,a与c交换,
即第0个元素分别与后续元素的交换
#include
#include
using namespace std;
void permutation(char* s, char* e)
{
if(*s == '\0')//出口
{
cout << e << endl;
}
else
{
int len = strlen(s);
for(int i = 0; i < len; i++)
{
if(i == 0 || s[0] != s[i]) //避开相同元素情况
{
swap(s[0], s[i]);
permutation(s+1, e);//交换完以后全排列子串
swap(s[0], s[i]);//交换回去
}
}
}
}
int main()
{
char s[] = {"abc"};
permutation(s, s);
cout << endl;
char a[] = "aac";
permutation(a, a);
return 0;
}
3、递归实现回溯算法
1、回溯的本质
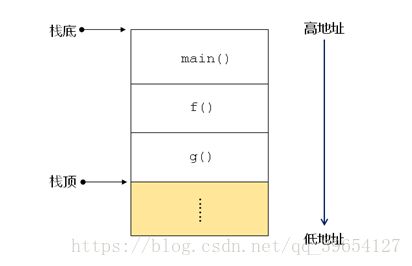
函数调用过程回顾
-程序运行后有一个特殊的内存区供函数调用使用
★ 用于保存函数中的实参,局部变量,临时变量,等
★ 从起始地址开始往—个方向增长(如:高地址→低地址)
★ 有—个专用“指针”标识当前已使用内存的“顶部”
这片特殊的内存区域符合了数据结构的栈特性,叫栈区
程序中的栈区:一段特殊的专用内存区
关于函数调用的深入分析https://blog.csdn.net/qq_39654127/article/details/80152476
2、逆序打印单链表中的偶数结点
实例分析:逆序打印单链表中的偶数结点
#include
using namespace std;
struct Node
{
int value;
Node* next;
};
Node* create_list(int v, int len)
{
Node* ret = NULL;
Node* slider = NULL;
for(int i = 0; i < len; i++)
{
Node* n = new Node();
n->value = v++;
n->next = NULL;
if(slider == NULL)
{
slider = n;
ret = n;
}
else
{
slider->next = n;
slider = n;
}
}
return ret;
}
void destory_list(Node* list)
{
while(list)
{
Node* del = list;
list = list->next;
delete del;
}
}
void print_list(Node* list)
{
while(list)
{
cout << list->value << "->";
list = list->next;
}
cout << "NULL" << endl;
}
void r_print_even(Node* list)
{
if(list != NULL)
{
r_print_even(list->next); //逆序打印后续子表
if((list->value) % 2 == 0)
{
cout << list->value << endl;
}
}
}
int main()
{
Node* list = create_list(2, 5);
print_list(list);
r_print_even(list);
destory_list(list);
return 0;
}
函数调用栈分析
退栈打印的过程其实就是回溯的过程
回溯法也称试探法,它的基本思想是:从问题的某一种状态(初始状态)出发,搜索从这种状态出发所能达到的
所有“状态”,当一条路走到“尽头”的时候(不能再前进),再后退一步或若干步,从另一种可能“状态”出发,继续
搜索,直到所有的“路径”(状态)都试探过。这种不断“前进”、不断“回溯”寻找解的方法,就称作“回溯法”。
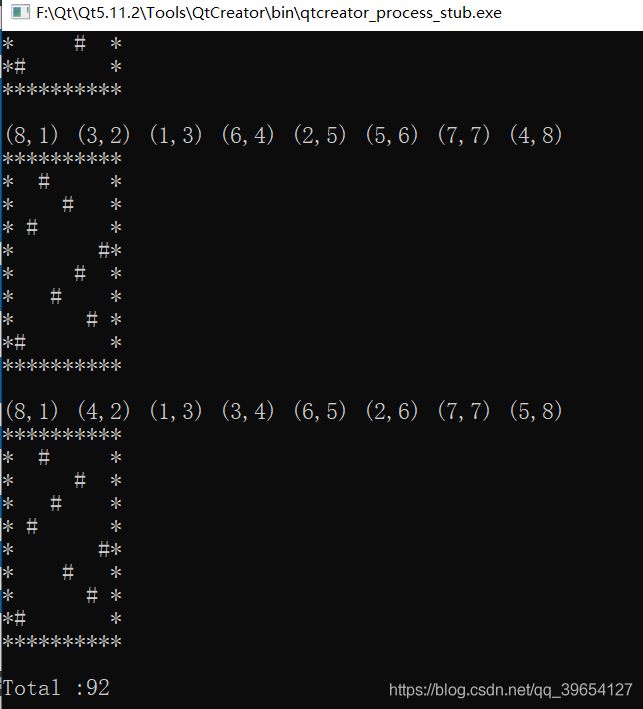
3、八皇后问题
八皇后问题
在—个8x8的国际象棋棋盘上,有8个皇后,每个皇后占一格;要求皇后间不会
出现相互“攻击”的现象(不能有两个皇后处在同—行、同—列或同—对角线上)。
关键数据结构定义:
-棋盘:二维数组(10 * 10)
0表示位置为空,1表示皇后,2表示边界
-位置:struct Pos;
struct Pos
{
int x;
int y;
};-方向: 当前位置数据加上方向数据
水平: (-1, 0), (1, 0)
垂直: (0, -1), (0, 1)
对角线: (-1, 1), (-1, -1), (1, -1), (1, 1)
算法思路
1. 初始化: j = 1
2. 初始化: i = 1
3. 从第j行开始,恢复i的有效值(通过函数调用栈进行回溯 ),判断第i个位置
a. 位置 i 可放入皇后:标记位置( i , j ) , j++, 转步骤2
b. 位置 i 不可放入皇后: i++, 转步骤a
c. 当i > 8时,j--,转步骤3
- 结束:
第8行有位置可放入皇后
编程实验
八皇后问题的递归解法 class QueueSolution;
#include
#include "LinkList.h"
using namespace std;
using namespace DTLib;
template
class QueueSolution
{
protected:
enum { N = SIZE + 2 };
struct Pos : public Object
{
Pos(int px = 0, int py = 0) : x(px),y(py) { }
int x;
int y;
};
int m_chessboard[N][N];
Pos m_direction[3];//只需要判断三个方向
LinkList m_solution;
int m_count;
void init()
{
m_count = 0;
//初始化边界
for(int i = 0; i < N; i += (N-1))
{
for(int j = 0; j < N; j++)
{
m_chessboard[i][j] = 2;
m_chessboard[j][i] = 2;
}
}
for(int i = 1; i <= SIZE; i++)
{
for(int j = 1; j <= SIZE; j++)
{
m_chessboard[i][j] = 0;
}
}
m_direction[0].x = -1;
m_direction[0].y = -1;
m_direction[1].x = 0;
m_direction[1].y = -1;
m_direction[2].x = 1;
m_direction[2].y = -1;
}
void print()
{
for(m_solution.move(0); !m_solution.end(); m_solution.next())
{
cout << "(" << m_solution.current().x << "," << m_solution.current().y << ") ";
}
cout << endl;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
{
switch(m_chessboard[i][j])
{
case 0: cout << " "; break;
case 1: cout << "#"; break;//皇后
case 2: cout << "*"; break;//边界
}
}
cout << endl;
}
cout << endl;
}
//检查三个方向上有没有别的皇后
bool check(int x, int y, int d)
{
bool flag = true;
do
{
x += m_direction[d].x;
y += m_direction[d].y;
flag = flag && (m_chessboard[x][y] == 0);
}
while( flag );
return (m_chessboard[x][y] == 2);
}
//检查第j行有没有可以放置皇后的位置
void run(int j)
{
if(j <= SIZE)
{
for(int i = 1; i <= SIZE; i++)
{
if(check(i, j, 0) && check(i, j, 1) && check(i, j, 2))
{
m_chessboard[i][j] = 1;//放置皇后
m_solution.insert(Pos(i, j));
run(j + 1);//下一行能不能放皇后
m_chessboard[i][j] = 0;//产生回溯
m_solution.remove(m_solution.length() - 1);
}
}
}
else
{
m_count++;//找到解决方案+1
print();
}
}
public:
QueueSolution()
{
init();
}
void run()
{
run(1);//从第一行开始放置皇后
cout << "Total :" << m_count << endl;
}
};
int main()
{
QueueSolution<8> qs;
qs.run();
return 0;
} 4、小结
递归是一种将问题分而自治的思想
用递归解决问题首先要建立递归的模型
递归解法必须要有边界条件,否则无解
不要陷入递归函数的执行细节,学会通过代码描述递归问题
程序运行后的栈存储区专供函数调用使用
栈存储区用于保存实参,局部变量,临时变量,等
利用栈存储区能够方便的实现回溯算法
八皇后问题是栈回溯的经典应用