VAE逻辑整理及VAE在异常检测中的小实验（附代码）

 本文主要讲解一下整个VAE变分推理在实践当中的逻辑，其中会结合案例讲一讲在实践当中VAE变分推理遇到的一些问题，在实践当中一些代码的写法以及公式在实践里的一些变式。有一些个人理解，如果有误欢迎大家一起指正讨论~！

Variance和control variate

 在VAE推导中，造成比较大的variance的项主要是
$$\zeta (\theta ,\varphi ;x^{(i)})=-D_{KL}(q_{\varphi }(z|x^{(i)})||p_{\theta }(z))+E_{q_{\varphi }(z|x^{(i)})}[\log p{}_{\theta }(x^{(i)}|z)]$$
当中$E_{q_{\varphi }(z|x^{(i)})}[\log p{}_{\theta }(x^{(i)}|z)]$这一项，其主要原因是这一项的期望为0，但方差却受一个随机的$p{}_{\theta }(x^{(i)}|z)$的波动影响，这就导致了在实验当中迭代收敛方向不确定，导致了迭代收敛速度慢。

两种常见的分类器

 论文Auto-Encoding Variational Bayes中为我们介绍了两种比较常见的分类器，一种是Bernoulli MLP作为decoder，Gaussian MLP作为encoder，另外一种则是Gaussian MLP作为分类器的encoder和decoder。对于离散型的情况，比如常见的Minst数据集应当选择Bernoulli MLP作为分类器。这主要是和数据的类型有关，对于Minst数据集它是binary的，所以为它设计的$p(x|z)$的格式就应当是Bernoulli分布更加合理一些。而对于一些连续型的数据集，我们应该设计成Gaussian分布。实验当中用到了一个叫做KDD99的数据集，该数据集绝大多数维数都是二元的，但是有少数维数是连续的，我们对用Bernoulli MLP作为decoder和Gaussian MLP作为decoder分别进行了一些实验。

相应代码

Minst数据集的训练和重构

from __future__ import print_function
import argparse
import torch
import torch.utils.data
from torch import nn, optim
from torch.nn import functional as F
from torchvision import datasets, transforms
from torchvision.utils import save_image
import numpy as np
import os

parser = argparse.ArgumentParser(description='VAE MNIST Example')
parser.add_argument('--batch-size', type=int, default=128, metavar='N',
                    help='input batch size for training (default: 128)')
parser.add_argument('--epochs', type=int, default=20, metavar='N',
                    help='number of epochs to train (default: 10)')
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='enables CUDA training')
parser.add_argument('--seed', type=int, default=128, metavar='S',
                    help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                    help='how many batches to wait before logging training status')
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()

torch.manual_seed(args.seed)

device = torch.device("cuda" if args.cuda else "cpu")

kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}

transform=transforms.Compose([transforms.ToTensor()])
data_train = datasets.MNIST('MNIST_data/', train=True, transform=transform, download=True)
data_test = datasets.MNIST('MNIST_data/', train=False, transform=transform)
train_loader = torch.utils.data.DataLoader(dataset=data_train, batch_size=args.batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=data_test, batch_size=args.batch_size, shuffle=True)

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1=nn.Linear(784,400)
        self.fc21=nn.Linear(400,20)
        self.fc22=nn.Linear(400,20)
        self.fc3=nn.Linear(20,400)
        self.fc4=nn.Linear(400,784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5*logvar)
        eps = torch.randn_like(std)
        return mu + eps*std

    def decode(self, z):
        h2=F.tanh(self.fc3(z))
        y=F.sigmoid(self.fc4(h2))
        return y

    def forward(self, x):
        mu1, logvar1 = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu1, logvar1)
        y=self.decode(z.view(-1,20))
        return  mu1, logvar1, y
    
   
model = VAE()
optimizer = optim.Adam(params = model.parameters (), lr=1e-3)



def loss_function(x, mu1, logvar1,y):
    
    MLD=-torch.sum(x.view(-1,784)*torch.log(y.view(-1,784))+(1-x.view(-1,784))*torch.log(1-y.view(-1,784))#MLD代表利用marginal likelihood 预测得到的误差
    #MLD=F.binary_cross_entropy(y,x,reduction='sum')
    KLD = -0.5 * torch.sum(1 + logvar1 - mu1.pow(2) - logvar1.exp())

    return MLD + KLD

def compute_recon(x,mu2,logvar2):
    temp=((2*np.pi*logvar2.exp()).sqrt())*(((x.view(-1,118)-mu2).pow(2))/(2*logvar2.exp()))
    return torch.sum(temp,dim=1)

def train(epoch):
    print("======================TRAIN MODE======================")
    model.train()
    train_loss = 0
    for i, (data, labels) in enumerate(train_loader):
        data = data.to(device)
        optimizer.zero_grad()
        mu1, logvar1, y= model(data)
        loss = loss_function(data, mu1, logvar1,y)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        if i % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, i * len(data), len(train_loader.dataset),
                100. * i / len(train_loader),
                loss.item() / len(data)))

    print('====> Epoch: {} Average loss: {:.4f}'.format(
          epoch, train_loss / len(train_loader.dataset)))


def test(epoch):
	print("======================TEST MODE======================")
    model.eval()
    test_loss = 0
    for data, _ in test_loader:
        if args.cuda:
            data = data.cuda()
        data=data.to(device)
        mu1, logvar1, y = model(data)
        test_loss += loss_function(data, mu1, logvar1,y).item()       
    test_loss /= len(test_loader.dataset)
    x_concat = torch.cat([data.view(-1, 1, 28, 28), y.view(-1, 1, 28, 28)], dim=3)
    save_image(x_concat, os.path.join('reconst-{}.png'.format(epoch + 1)))
    print('====> Test set loss: {:.4f}'.format(test_loss))
    
if __name__ == "__main__":
    for epoch in range(0, args.epochs):
        train(epoch)
        test(epoch)

 对于MINST数据集我们可以得到一个重构的图片结果，在这里展示一下部分结果：

添加链接描述

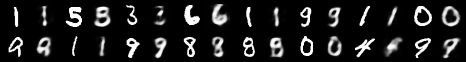
KDD99数据

 为了对比不同的处理，KDD99我们使用了Bernoulli MLP网络和Gaussian MLP网络分别做了测试观察了一下测试效果。KDD99没有去进行重构对比的意义，我们主要希望通过VAE神经网络对他进行异常检测。
 这里，论文Variational Autoencoder based Anomaly Detection using Reconstruction Probability这篇文章给出了相应的算法：

 算法当中将reconstruction probability作为了一个指标，利用它的取阈值来作为判断是否为异常点。
 方案一是利用Gaussian MLP代码如下：

from __future__ import print_function
import argparse
import torch
import torch.utils.data
from torch import nn, optim
from torch.nn import functional as F
from torchvision import datasets, transforms
from data_loader import get_loader
from torchvision.utils import save_image
import numpy as np

parser = argparse.ArgumentParser(description='VAE MNIST Example')
parser.add_argument('--batch-size', type=int, default=128, metavar='N',
                    help='input batch size for training (default: 128)')
parser.add_argument('--epochs', type=int, default=5, metavar='N',
                    help='number of epochs to train (default: 10)')
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='enables CUDA training')
parser.add_argument('--seed', type=int, default=1, metavar='S',
                    help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                    help='how many batches to wait before logging training status')
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()

torch.manual_seed(args.seed)

device = torch.device("cuda" if args.cuda else "cpu")

kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}

data_loader = get_loader('kdd_cup.npz', batch_size=128,mode='train')

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1=nn.Linear(118,60)
        self.fc21=nn.Linear(60,10)
        self.fc22=nn.Linear(60,10)
        self.fc3=nn.Linear(10,60)
        self.fc41=nn.Linear(60,118)
        self.fc42=nn.Linear(60,118)

    def encode(self, x):
        h1 = F.tanh(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5*logvar)
        eps = torch.randn_like(std)
        return mu + eps*std

    def decode(self, z):
        h2=F.tanh(self.fc3(z))
        return self.fc41(h2),self.fc42(h2)

    def forward(self, x):
        mu1, logvar1 = self.encode(x.view(-1, 118))
        z = self.reparameterize(mu1, logvar1)
        mu2,logvar2=self.decode(z.view(-1,10))
        return  mu1, logvar1, mu2, logvar2

model = VAE()
optimizer = optim.Adam(params = model.parameters (), lr=1e-3)

def loss_function(x, mu1, logvar1,mu2,logvar2):
    MLD=torch.norm((((2*np.pi*logvar2.exp()).sqrt())*(((x.view(-1,118)-mu2).pow(2))/(2*logvar2.exp()))),dim=1)
    MLD=torch.sum(MLD)
    KLD = -0.5 * torch.sum(1 + logvar1 - mu1.pow(2) - logvar1.exp())

    return MLD + KLD

def compute_recon(x,mu2,logvar2):
    temp=((2*np.pi*logvar2.exp()).sqrt())*(((x.view(-1,118)-mu2).pow(2))/(2*logvar2.exp()))
    return torch.sum(temp,dim=1)

def train(epoch):
    print("======================TRAIN MODE======================")
    model.train()
    train_loss = 0
    for i, (data, labels) in enumerate(data_loader):
        data = data.to(device)
        optimizer.zero_grad()
        mu1, logvar1, mu2, logvar2 = model(data)
        loss = loss_function(data, mu1, logvar1, mu2,logvar2)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        if i % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, i * len(data), len(data_loader.dataset),
                100. * i / len(data_loader),
                loss.item() / len(data)))

    print('====> Epoch: {} Average loss: {:.4f}'.format(
          epoch, train_loss / len(data_loader.dataset)))


def test():
    print("======================TEST MODE======================")
    data_loader=get_loader('kdd_cup.npz',batch_size=128,mode='test')
    model.eval()
    train_recon = []#这里按照论文用了reconstruction probability作为评级指标
    train_labels = []
    for it, (data, labels) in enumerate(data_loader):
        data = data.to(device)
        mu1,logvar1,mu2,logvar2=model(data)
        sample_recon=compute_recon(data,mu2,logvar2)
        train_recon.append(sample_recon.data.cpu().numpy())
        train_labels.append(labels.numpy())
  

    
    train_recon  = np.concatenate(train_recon,axis=0)        
    train_labels = np.concatenate(train_labels,axis=0)

    test_recon  = []
    test_labels = []
    for it, (data, labels) in enumerate(data_loader):
        data = data.to(device)
        mu1,logvar1,mu2,logvar2=model(data)
        sample_recon  = compute_recon(data,mu2,logvar2)
        test_recon.append(sample_recon.data.cpu().numpy())
        test_labels.append(labels.numpy())


    test_recon = np.concatenate(test_recon,axis=0)
    test_labels = np.concatenate(test_labels,axis=0)
    
    
    print("利用论文准则进行评价")
    thresh = np.percentile(test_recon,100-20)
    print("Threshold :",thresh)
    pred = (test_recon > thresh).astype(int)
    gt=test_labels.astype(int)
    from sklearn.metrics import precision_recall_fscore_support as prf, accuracy_score
    
    accuracy = accuracy_score(gt,pred)
    
    precision, recall, f_score, support = prf(gt,pred,average='binary')
    print("Accuracy : {:0.4f}, Precision : {:0.4f}, Recall : {:0.4f}, F-score : {:0.4f}".format(accuracy, precision, recall, f_score))
    from sklearn import metrics
    test_auc= metrics.roc_auc_score(gt,pred)
    print("AUC :{:0.4f}".format(test_auc))

if __name__ == "__main__":
    for epoch in range(1, args.epochs + 1):
        train(epoch)
    test()

 上图是利用Gaussian MLP得到的LOSS的效果，可以看出loss在收敛。
 利用Gaussian MLP得到的结果如下：
 其F1值达到了0.6825，AUC也达到了0.7598，就是利用此方案所选择的阈值比较小，但是其实分类的效果还是可以接受的。基本复现了原论文中的效果。
 方案二是考虑到连续值较少，所以利用了Bernoulli MLP模型。
可以看出其效果也不错，loss有明显减少。

 不过在一段时间过后出现了loss为nan的情况，目前原因还不明确，所以说明对于含连续型参量的问题还是应该使用Gaussian MLP网络来进行解决。