汉诺塔的分析

汉诺塔是递归中最经典的问题之一，但是有很多小伙伴对于汉诺塔不理解，到最后直接跳过或者对于代码死记硬背，接下来我谈一谈我对于汉诺塔及递归的理解。

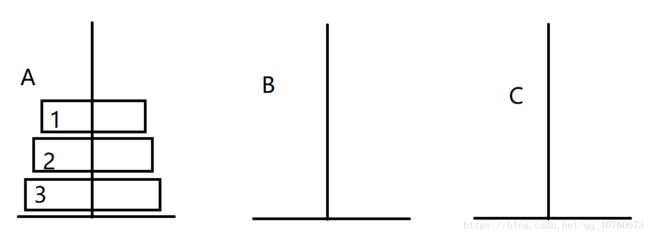
问题描述：该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

首先我们从最简单的只有两个盘子进行分析。步骤分为三步：

1.  1号盘 A-》B

2.  2号盘 A-》C

3.  1号盘 B-》C

现在我们对其进行拓展到三个盘子在进行分析：

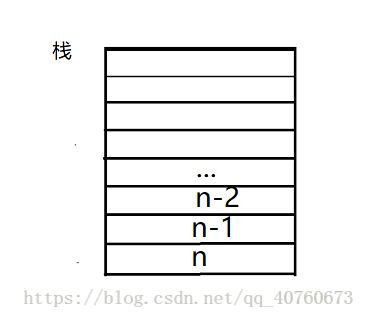
这里我不对3个盘子的具体移动进行分析，我先对这个三个盘子的划分做一点改变在进行讨论，改变如下图。

这里我把最底下的盘子设置为n盘子，出n盘子以上的全部盘子设置为（n-1）盘子，这个时候操作就和我们之前的最简单只有两个盘子的情况相似了，在抽象上理解只需要执行3步操作就可以完成：（实际执行不止三步）

1.  n-1盘 A-》B

2.  n盘 A-》C

3.  n-1号盘 B-》C

在知道这几点后我们接下来就可以写代码了：

#include

 

void Print (char from, char to, int num) {                       //形参列表（起始柱子，目标柱子，第num个盘子）

          printf("第%d个盘子 %c -->> %c \n", num, from, to);

}

void Move(char a, char b, char c, int n){                         //形参列表（起始柱子，过度柱子/缓冲柱子，目标柱子，第n盘）

          if (n == 1)

                   Print(a,c,n);                         //第n个盘子从起始柱子移动到到目标柱子

          else {

                   Move(a,c,b,n-1);            //1. n-1盘 A-》B

                   Print(a,c,n);                         //2.  n盘 A-》C

                   Move(b,a,c,n-1);            //3. n-1号盘 B-》C

          }

}

int main() {

          char a, b, c;

          int n;

 

          a = 'A', b = 'B', c = 'C';                             

          printf("请输入有几个盘子要移动：");

          scanf("%d",&n);

          Move(a,b,c,n);

}

代码很简单，上网一搜到处都是差不多的。但是这个比较抽象，有很多小伙伴没有真正的理解。当他们仔细一看，对代码进行模拟的时候发现盘子移来移去，不知道哪个打哪个。下面我就自己的理解分析一下。

首先我对刚才的分析换一个描述，完成操作分三步：

1.移动n-1的盘子做好准备工作，保证可以移动第n盘子。（移动盘子要求始终保持 大盘子在下小盘子在上）

2.移动n盘子从起始柱子到目标柱子

3.移动n-1的盘子到n盘子的柱子上

这样的三步一样完成了操作，但是我没有把具体的把a，b，c柱子上的盘子从哪个柱子移动到哪去，而是用了从起始柱子到目标柱子。第一种的描述是为了让你们能容易理解，所以用a，b，c柱子实例化来代替。现在从抽象的角度和分析代码编写的角度来分析，对于汉诺塔的代码我们实际做的操作就是把第n个盘子从起始柱子移动到目标柱子。因此，我们需要传入参数 起始柱子 目标柱子 第n个盘子 还有中间柱子，这些在写任何递归之前一定要分析清楚。接下来我对上面重新描述的操作重新分析（注：下面的操作会用到 栈 这种数据结构来表示，又兴趣的小伙伴可以去了解一些，反正迟早要学!）

我把递归模拟成一层层的，每进入一次递归就向上开拓一层，每一层都保存当前自己的状态。文字描述有点抽象，下面我们用图片模拟一下。

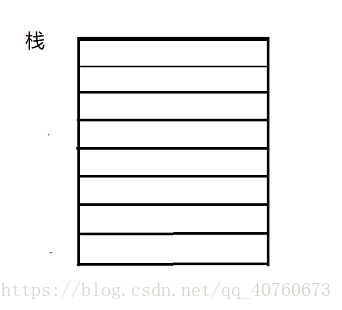
这是一个栈，，每进入一次递归就向上开拓一层（压栈）：

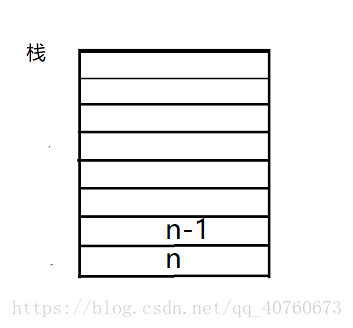
首先从入口函数mian（）开始调用Move（）函数。我们把当前第n个盘子压入栈中（如下图），这个时候我们第n个盘子还没开始移动，需要n-1的所有盘子进行准备工作，即进入递归。这个时候我们调用Move（）递归函数把对第n-1个盘子移动的操作压入栈中。（如下图）

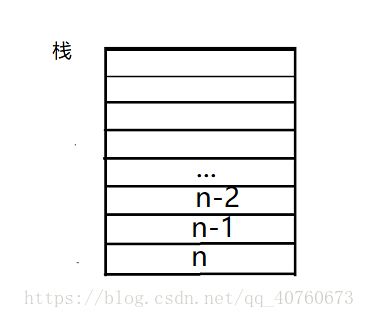
要移动第n-1个盘子，又需要n-2的所有盘子做准备工作，这个时候我们调用Move（）递归函数把对第n-2个盘子移动的操作压入栈中。以此类推，后面的操作基本相同，直到为第1个盘子，则无需进入递归函数Move（）（只有一个盘子不用做准备工作），直接从起始柱子移动到目标柱子。

（假设当前是这n-2盘子这一层）n-2盘子这一层的准备工作已经完成，即n-2这一层的函数第一个递归函数Move（）结束。既然有压栈（入栈），那就有出栈，刚刚提到n-2这一层的准备工作完成，即第一个Move（）函数结束后，那就执行出栈即将n-3的层数清空，那么n-2当前状态为（如下图）。准备工作完成后就开始移动第n-2的盘子即执行Print（），将第n-2个盘子从起始柱子移动到目标柱子。

我们递归函数Move（）总共有三步，（当前是这n-2盘子这一层）现在还有最后一步Move（）操作将n-3的所有盘子从起始柱子移动到目标柱子，执行了Move（）故要进行压栈，即重复之前的压栈操作（如下图），要对第n-3个盘子进行移动，则需要做准备工作，与之前的操作相同一样是分三步进行。所有的对于完成所有的操作全都可以用这三步来进行模拟，直到操作完成。

以上就是我对于汉诺塔从简单到深入的分析。本人小白第一次写博客，欢迎提出建议和指出错误。