高精度计算(三)压位

高精压位

继承咱们(一)上的例题…A+B+C 链接

有兴趣的可以用上一篇的内容做一下这道神题

不出意外的话会出现下面的字样 Time Limit Exceeded ……

我们需要用一种特殊的技巧对上算法进行处理

压位思想

还记得我们存储数字的方式？

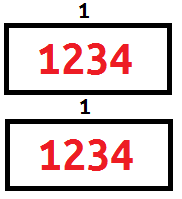
举个栗子:1234 + 1234这是之前的存储方式

实际上我们一个数组空间(int)是可以储存 2147483647 以下的数字 这样非常浪费 而且以上存储方式需要按位相加最后的计算次数是4

现在考虑这样的存储方式

这样相对上面的存储方式来说利用度较高 

理解方式：考虑二进制 十进制 十六进制 的计算方式 满2进1 满10进1 满16进1

那么以上的存储方式请理解为100进制的计算 也就是满100进1

按照这样储存 按照(二)的规则计算 就是把1和2 3和4压到了同一个数组空间里 叫做压位

这样存储的数字计算次数就变成了2 很厉害的优化……

那我们为什么不这样呢

没错这是10000进制……

计算次数变成了1 其实仔细看一下就知道压位的思想就是把本来不用高精的计算尽量的扩大

来达到减少计算次数的目的

特殊的输出

在最后的输出答案部分 需要一些处理(下面假设写压P位的高精(也就是把P个数压到同一个数组空间里))

一句话概括：除最高位外,一切不足P位的数字输出时需要在前面补上0使得满足P位

比如压2位 2 + 99 为例 最后会用到两个数组空间(一个放1，一个放1…)但是这两个一代表的意义不同，

第二个可以原样输出因为这是最高位(即整个数的长度modP后得到的剩余部分 这一部分是独立于其他部分的 如果补上0 最后就是0101 是不对的)，第一个就需要补上一个0来使得输出101而不是11

那么怎么实现呢 下面代码

代码实现

习惯写很多注释 在这里不多做解释

#include 
#include 
#include 
#include 

#define p 8//要压的位数 
#define carry 100000000//相应的10的P次方 用于进位 
//这样如果要改变压位的位数只要改这里就可以 
using namespace std;

const int Maxn=50001;

char s1[Maxn],s2[Maxn];
int a[Maxn],b[Maxn],ans[Maxn];

int change(char s[],int n[])//压位的核心部分 
{
	char temp[Maxn];//中间变量 记录每p位的数 
	int len=strlen(s+1),cur=0;
	while(len/p){//如果len大于等于p 
		strncpy(temp,s+len-p+1,p);//从后面截出来p位数 
		n[++cur]=atoi(temp);//把temp搞成数字 
		len-=p;//继续下p位 
	}
	if(len){//如果最后len不是正好p的倍数 也就是还剩下点不够p位的 
		memset(temp,0,sizeof(temp));
		strncpy(temp,s+1,len);//全截下来 
		n[++cur]=atoi(temp);//赋上 
	}
	return cur;//返回一个位数 
}
//这里就是(二)中的内容了 计算正常计算就行 
int add(int a[],int b[],int c[],int l1,int l2)
{
	int x=0,l3=max(l1,l2);
	for(int i=1;i<=l3;i++){
		c[i]=a[i]+b[i]+x;
		x=c[i]/carry;//进位 
		c[i]%=carry;
	}
	while(x>0){c[++l3]=x%10;x/=10;}
	return l3;//返回答案的位数 
}

void print(int a[],int len)
{ 
	printf("%d",a[len]);//处理高位 
	for(int i=len-1;i>=1;i--)printf("%0*d",p,a[i]);//输出p位 不足补0 
	printf("\n");
}

int main()
{
//	freopen("t.in","r",stdin);
//	freopen("t.out","w",stdout);
	scanf("%s%s",s1+1,s2+1);//读入两个字符串 

	int la=change(s1,a);//将s1这个字符串转化为a这个整型数组 
	int lb=change(s2,b);//同上 
	
	int len=add(a,b,ans,la,lb); 
	//计算长度为la的a数组和长度为lb的b数组最后把答案赋给ans数组 并顺便计算出ans的长度(便于输出) 
	print(ans,len);//输出函数 
}

欢迎指出Bug

End。