机器学习2：朴素贝叶斯分类器Naïve Bayes Classifier（基于R language&Python）

  朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法（朴素贝叶斯法与贝叶斯估计是不同的概念）。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对个给定的输入 $x$，利用贝叶斯定理求出后验概率最大的输出 $y$。朴素贝叶斯方法实现简单，学习与预测的效率都很高，是一种常用的方法¹。

  假如对于机器学习是用来干什么的也不是很清楚的话，可以先阅读一下周志华老师的西瓜书（清华大学出版社）或者李航老师的统计学习方法（清华大学出版社）。可以粗糙地理解为，机器学习是通过一些已知结果的样本来训练一个训练器，再将这个训练器运用到未知结果的样本上，用以推测其结果。我们在机器学习中通常要做的就是预测问题、参数优化问题和模型比较问题。

还有阿里云大学上的免费公开课：https://edu.aliyun.com/course/838?spm=5176.13345299.1392555.36.458ef153vkLC1h

基本原理方法

模型目标

  设输入空间（又称样本空间、属性空间） $\mathcal{X}\subseteq {\mathbb{R}}^n$ 为 $n$ 维向量的集合，输出空间为类别标记的集合 $\mathcal{Y}=\{C_1,C_2,\cdots ,C_K\}$。输入为特征向量 $x\in \mathcal{X}$，输出为类标记 $y\in \mathcal{Y}$。$X$ 是定义在输入空间 $\mathcal{X}$ 上的随机变量，$Y$ 是定义在输出空间 $\mathcal{Y}$ 上的随机变量。

  首先，我们需要确定一个损失函数，将最小化该损失函数的期望值（即，最小化期望风险函数）作为建模目标：期望风险越小，说明模型预测结果和真实结果越相近。不妨考虑 0-1 损失函数作为损失函数的例子：

$$L(Y,f(X))=\{\begin{array}{ll}0,& f(X)=Y,\\ 1,& f(X)\ne Y.\end{array}$$

这里 $f(X)$ 为预测值，$Y$为真实类别值。这个损失函数意味着，当样本的模型预测结果和真实类别一致时，损失函数值为0；样本的模型预测结果和真实类别不一致时，损失函数值为1。

  其次，期望风险/平均损失(Expected Prediction Error,EPE) 可以写作：

$$E[L(Y,f(X))]$$

其中，

$$L(Y,f(X))=\{\begin{array}{ll}0,& f(X)=Y,\\ 1,& f(X)\ne Y.\end{array}$$

  根据重期望公式，EPE可以分解为：

$$E[L(Y,f(X))]=E_X[E_{Y|X}[L(Y,f(X))]]$$

  最后，我们寻找的朴素贝叶斯训练器 $f(\cdot )$ 要能够最小化EPE。为了最小化 EPE，我们找到了一个它的充分条件：在 $X=x$ 给定情况下，让 $E_{Y|X=x}[L(Y,f(X))]$ 都达到最小。能达到这个条件，就足以达到最小化 EPE 的目的。该充分条件可以表达为：

$$\begin{array}{rl}& argmin{E}_{Y|X=x}[L(Y,f(X))]\\ =& argmin0\cdot P(L(Y,f(X))=0|X=x)+1\cdot P(L(Y,f(X))=1|X=x)\\ =& argmin0\cdot P(f(X)=Y|X=x)+1\cdot P(f(X)\ne Y|X=x)\\ =& argmin1-P(f(X)=Y|X=x)\\ =& argmaxP(f(X)=Y|X=x)\end{array}$$

  因此，基于最小化EPE的最优贝叶斯训练器 $f(\cdot )$ 要满足以下条件：

$$\begin{array}{rl}f(x)=& argmaxP(f(X)=Y|X=x)\\ =& argma{x}_{k\in \{1,2,\cdots ,K\}}P(f(X)=C_k|X=x)\end{array}$$

这是寻找最优训练器的后验概率最大化准则。根据这个准则，得到的训练器 $f(\cdot )$ 对于输入 $X=x$ 得到的训练结果分类为：使条件概率 $P(f(X)=C_k|X=x)$ 取值最大的那个分类 $C_k$。 比如 $i,j\in \{1,2,\cdots ,K\}$，若

$$P(f(X)=c_i|X=x)>P(f(X)=c_j|X=x)$$

则 $X=x$ 通过得到训练器 $f(\cdot )$ 的训练结果分类为第 $i$ 类。

贝叶斯错误 Bayes error

  贝叶斯分类器的错误率称为贝叶斯错误。理论上，贝叶斯分类器是基于“后验概率最大化准则”进行分类的最优分类器，因此，贝叶斯错误常用来作为比较其他分类器效果如何的基底。

模型假设

  朴素贝叶斯分类器是一系列基于贝叶斯定理的简单概率分类器，输入空间需要满足假设：在特征（又称属性）之间具有很强的相互独立性，需注意这是一种条件独立性（下文会解释）。

概率模型 Probabilistic Model

  给定一个分类实例问题，用向量 $X=(x^{(1)},x^{(2)},\cdots ,x^{(m)})$ 来表示 $m$ 个属性/特征的输入。利用贝叶斯定理，条件概率 $P(f(X)=C_k|X=x)$ 可以分解为：

$$P(f(X)=C_k|X=x)=\frac{P(f(X)=C_k)p(X=x|f(X)=C_k)}{P(X=x)}$$

简记为

$$p(C_k|x)=\frac{p(C_k)p(x|C_k)}{p(x)}=\frac{p(C_k,x)}{p(x)}$$

其中的原理即

$$posterior（后验分布）=\frac{prior（先验分布）\times likelihood（可能性）}{evidence}$$

  实际上，我们仅需关注该分数的分子，因为分母“evidence”是给定 $x$ 之后能够确定下来的常数。在贝叶斯定理中 $p(x)={\sum }_{k=1}^{K}p(c_k)p(x|c_k)$，即在不同类别 $c_k$ 下，可能会出现属性/特征 $x$ 的可能性，对于我们给定的属性/特征 $x$，$p(x)$也是一定的。

  因此，在比较 $p(C_i|X=x)$ 和 $p(C_j|X=x)$ 大小时，若“去除相同的分母 $p(x)$”直接比较 $p(C_i,x)$ 和 $p(C_j,x)$ 大小，结果也是一样的。

  我们来考虑 $p(C_k,X)$ 的估计，根据条件概率乘法公式的推广，可得：

$$\begin{array}{rl}p(C_k,X)=& p(C_k)p(x^{(1)},x^{(2)},\cdots ,x^{(m)}|C_k)\\ =& p(C_k)p(x^{(1)}|C_k)p(x^{(2)}|C_k,x^{(1)})\cdots p(x^{(m)}|C_k,x^{(1)},x^{(2)},\cdots ,x^{(m-1)})\end{array}$$

  由“朴素贝叶斯”的不同属性/特征的条件独立性假设可知，给定类别 $C_k$，假设每个特征 $x_i$ 条件独立于每个其他特征 $x_j$ 。这意味着：

$$\begin{array}{rl}p(x^{(2)}|C_k,x^{(1)})=& p(x^{(2)}|C_k)\\ \cdots & \\ p(x^{(m)}|C_k,x^{(1)},x^{(2)},\cdots ,x^{(m-1)})=& p(x^{(m)}|C_k)\end{array}$$

  关于朴素贝叶斯的独立性，我们用一个例子来解释：如果水果是红色，圆形且直径约10厘米，则可以认为是苹果。朴素贝叶斯分类器的“独立性”便认为无论颜色、形状和直径这三个特征之间是否存在任何相关性，每一个特征都会独立地影响这种水果是否被归为苹果的可能性。

  因此，联合模型可以表示为

$$p(C_k|x)=\frac{p(C_k,x)}{evidence}\propto p(C_k,x)=p(C_k)\prod _{i=1}^{m}p(x^{(i)}|C_k)$$

  那么朴素贝叶斯分类器就是为 $\hat{y}=C_k$ 分配类标签 $k$ 的函数，如下所示：

$$f(x)=\hat{y}=argma{x}_{k\in \{1,2,\cdots ,K\}}p(C_k)\prod _{i=1}^{m}p(x^{(i)}|C_k)$$

事件模型 Event Model

  $p(x^{(i)}|C_k)$ 被称为事件模型。

连续事件模型

高斯朴素贝叶斯 Gaussian Naïve Bayes

  高斯朴素贝叶斯训练器的事件模型为：

$$p(x=v|c)=\frac{1}{\sqrt{2\pi {\sigma }_c^2}}{e}^{-\frac{(v-{\mu }_c{)}^2}{2{\sigma }_c^2}}$$

其中不同类别 $c$ 下 ${\sigma }_c$ 和 ${\mu }_c$ 会改变。

离散事件模型

贝努利贝叶斯 Bernoulli Naïve Bayes

  贝努利朴素贝叶斯训练器的事件模型为：
$$p(x^{(j)}=l|c_k)=p_{kj}^l(1-p_{kj}{)}^{1-l},l=0,1$$

其中 $p_{kj}$ 为在类别 $c_k$ 下事件 $x^{(j)}$ 发生的概率。

多项式贝叶斯 Multinomial Naïve Bayes

  多项式朴素贝叶斯训练器的事件模型为：
$$p(x^{(j)}=l|c_k)=p_{kjl}$$

多项式朴素贝叶斯分类器在对数空间中表示时变为线性分类器。

概率估计

特征/属性取值是离散值

  根据概率模型

$$f(x)=\hat{y}=argma{x}_{k\in \{1,2,\cdots ,K\}}p(C_k)\prod _{i=1}^{m}p(x^{(i)}|C_k)$$

可知我们需要估计两个量：一个是类别为 $C_k$ 的可能概率 $\hat{P}(Y=C_k)$ ；另一个是输入特征的第 $j$ 个特征 $X^{(j)}=l$ 的条件概率 $\hat{P}(X^{(j)}=l|C_k)$

极大似然估计 Maximum Likelihood Esitimation,MLE

  先验概率的极大似然估计为：

$$\hat{P}(Y=C_k)=\frac{{\sum }_{i=1}^{n}I(y_i=C_k)}{n}$$

其中 $I(\cdot )$ 为示性函数。

  这个公式的含义是：${\sum }_{i=1}^{n}I(y_i=C_k)$ 表示在训练集中，样本类别为 $C_K$ 的样本数量，$n$ 表示样本总数，因此，$\frac{{\sum }_{i=1}^{n}I(y_i=C_k)}{n}$ 表示已有训练集中样本的类别为 $C_K$ 的比例。

  每个类别为 $C_k$ 的样本中，第 $j$ 个特征为第 $l$ 种取值的条件概率的极大似然估计为：

$$\hat{P}(X^{(j)}=l|C_k)=\frac{{\sum }_{i=1}^{n}I(x_i^{(j)}=l,y_i=C_k)}{{\sum }_{i=1}^{n}I(y_i=C_k)}$$

  这个公式的含义是：${\sum }_{i=1}^{n}I(x_i^{(j)}=l,y_i=C_k)$ 表示在训练集中，样本类别为 $C_K$ 同时第 $j$ 个特征为第 $l$ 种取值的样本数量，${\sum }_{i=1}^{n}I(y_i=C_k)$ 表示在训练集中，因此，$\frac{{\sum }_{i=1}^{n}I(x_i^{(j)}=l,y_i=C_k)}{{\sum }_{i=1}^{n}I(y_i=C_k)}$ 表示训练集样本类别为 $C_K$ 的样本中，第 $j$ 个特征为第 $l$ 种取值的样本比例。

  但是，由极大似然估计定义的条件概率可能为0，那么带入到概率模型中去，${\prod }_{i=1}^{m}p(x^{(i)}|C_k)=0$，此时，其他维度的条件概率无论是否为0，都将失去意义。为修正这个问题，我们将采用贝叶斯估计

贝叶斯估计 Baysian Esitimation

  条件概率的贝叶斯估计为：

$$\hat{P}(X^{(j)}=l|C_k)=\frac{{\sum }_{i=1}^{n}I(x_i^{(j)}=l,y_i=C_k)+\lambda }{{\sum }_{i=1}^{n}I(y_i=C_k)+S_j\lambda }$$

其中 $\lambda >0$，当 $\lambda =0$ 这就是MLE，常取$\lambda =1$ ，这时称之为拉普拉斯光滑(Laplace smoothing)。这是一个小样本校正，称为伪计数，修正后不会将任何条件概率值正好为零。$S_j$ 为第 $j$ 个特征可能的取值总数，它的作用是保证第 $j$ 个特征不同取值的条件概率之和为1（正规性），即

$$\sum _{l=1}^{S_j}\hat{P}(X^{(j)}=l|C_k)=1.$$

  同样，先验概率的贝叶斯估计为：

$$\hat{P}(Y=C_k)=\frac{{\sum }_{i=1}^{n}I(y_i=C_k)+\lambda }{n+K\lambda }$$

其中 $K$ 为总的类别数，它的作用也是保证先验概率的正规性。

特征/属性取值是连续值

  有两种方法来估计属性的类条件概率，一是把每一个连续的属性离散化，然后用相应的离散区间来替换连续属性值；二是采用前述的高斯函数来估计类条件密度函数，

$$p(x=v|c)=\frac{1}{\sqrt{2\pi {\sigma }_c^2}}{e}^{-\frac{(v-{\mu }_c{)}^2}{2{\sigma }_c^2}}$$

其中不同类别 $c$ 下 ${\sigma }_c$ 和 ${\mu }_c$ 会改变，这样生成的朴素贝叶斯模型就是高斯朴素贝叶斯模型。

朴素贝叶斯模型特点

目标		关键的几个问题	是否需要标准化	是否容许有缺失值
分类判别(因变量定性)	回归(因变量定量)
可以	不可以	（1）	不需要	容许
		（2）密度函数
		（3）先验概率

优点

• 与其他先进的训练模型（如，支持向量机）相比也有一定的竞争力
• 计算迅速
• 可以避免数据维数太高带来的麻烦，朴素贝叶斯将问题都转化为一维的
• 可扩展性强（可扩展性好指的是加入新数据后，只要对原模型做些许修改就可以继续使用）
• 所需训练集既可以是小批量的也可以是大批量的

缺点

• 由于现实中类别条件概率的独立性未必成立，所以预测不是很准确
• 对于具有大量特征的训练集不理想

朴素贝叶斯模型评估

解释²：

• Natural handling of data of “mixed” type：混合型数据处理能力。混合型数据指的是数据集的特征既有定性变量也有定量变量，朴素贝叶斯模型可以训练这样的数据集，但需注意的是输出必须是定性变量（即，只能做分类问题）；
• Handling of missing values：缺失值处理能力。朴素贝叶斯模型可以训练包含缺失值的数据集，从前面的例子也可以看出，缺失值只会影响计数当中少几个计数，但是概率的估计不会受到影响；
• Robustness to outliers in input space：异常值的稳健型。朴素贝叶斯模型会受异常值的影响，这是因为会影响类条件概率，但影响效果适中；
• Insensitive to monotone transformations of inputs：对单调性变换不敏感；
• Computational scalability：可扩展性。可扩展性好指的是加入新数据后，只要对原模型做些许修改就可以继续使用，朴素贝叶斯模型的可扩展性比较好；
• Ability to deal with irrelevant inputs：处理无关解释变量的能力。朴素贝叶斯模型无法甄别无关变量，不能将无关变挑出来剔除，处理无关变量能力比较差；
• Ability to extract linear combinations of features：获得特征的线性组合能力；
• Interpretability：可解释性。朴素贝叶斯可解释性不强（对于这点，博主不太同意，这明明就是最好理解的嘛！从条件概率出发）；
• Predictive power：预测能力。朴素贝叶斯预测能力中等。

手动计算的朴素贝叶斯分类器

  实例：探讨各项因素对是否能进行高尔夫运动的影响。

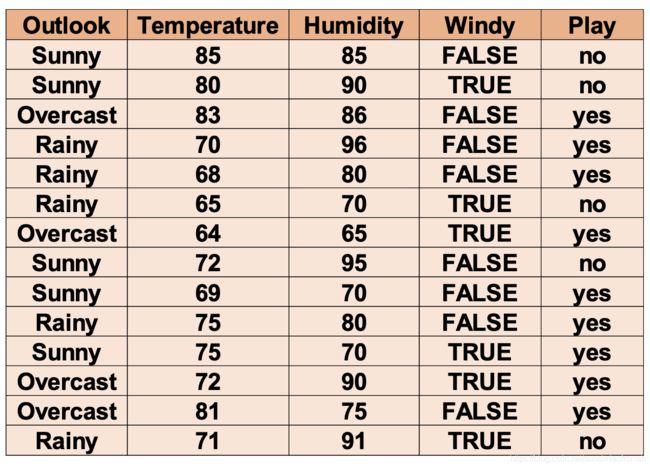
例：图中是golf例子的训练集，我们只考虑"Outlook"和"Windy"这两个特征，利用Laplace光滑的贝叶斯估计来训练参数，预测事件"x=(Outlook=Overcast,Windy=FALSE)"类别为"yes"和"no"的概率。

解：我们首先做两张下面这样的表格：

Play(类别因变量)	Outlook(特征)			总计数
	Overcast	Sunny	Rainy
no	0	3	2	5
yes	4	2	3	9

Play(类别因变量)	Windy(特征)		总计数
	FALSE	TRUE
no	2	3	5
yes	6	3	9

  解释一下这张表中数字的意思：比如第一张表中的“2”代表，类别因变量为“no”的样本里有2个样本在“Overlook”特征上取“FALSE”。其他数字的定义诸如此类。

  记 $C_1=yes,C_2=no$，"Overlook"的三个取值：$l_1=Sunny,l_2=Overcast,l_3=Rainy$，"Windy"的三个取值：$l_1=FALSE,l_2=TRUE$。

  我们的目的是预测事件"x=(Outlook=Overcast,Windy=FALSE)"类别，因此 $x^{(1)}=l_2=Overcast,x^{(2)}=l_1=FALSE$。由于Laplace光滑，因此 $\lambda =1$，总样本数 $n=14$。

$j=1,x^{(1)}$代表"Overlook"特征的取值，$S_1=3$：

$$\begin{array}{rl}\hat{P}(x^{(1)}=l_2|C_1)=& \frac{{\sum }_{i=1}^{14}I(x_i^{(1)}=l_2,y_i=C_1)+1}{{\sum }_{i=1}^{14}I(y_i=C_1)+S_1}\\ =& \frac{4+1}{9+3}=\frac{5}{12}\\ \hat{P}(x^{(1)}=l_2|C_2)=& \frac{{\sum }_{i=1}^{14}I(x_i^{(1)}=l_2,y_i=C_2)+1}{{\sum }_{i=1}^{14}I(y_i=C_2)+S_1}\\ =& \frac{0+1}{5+3}=\frac{1}{8}\end{array}$$

$j=2,x^{(2)}$代表"Windy"特征的取值，$S_2=2$：

$$\begin{array}{rl}\hat{P}(x^{(2)}=l_1|C_1)=& \frac{{\sum }_{i=1}^{14}I(x_i^{(2)}=l_1,y_i=C_1)+1}{{\sum }_{i=1}^{14}I(y_i=C_1)+S_2}\\ =& \frac{6+1}{9+2}=\frac{7}{11}\\ \hat{P}(x^{(2)}=l_1|C_2)=& \frac{{\sum }_{i=1}^{14}I(x_i^{(2)}=l_1,y_i=C_2)+1}{{\sum }_{i=1}^{14}I(y_i=C_2)+S_2}\\ =& \frac{2+1}{5+2}=\frac{3}{7}\end{array}$$

  计算先验概率的贝叶斯估计：

$$\begin{array}{rl}\hat{P}(C_1)=& \frac{9+1}{14+2}=\frac{5}{8}\\ \hat{P}(C_2)=& \frac{5+1}{14+2}=\frac{3}{8}\end{array}$$

  因此，

$$\begin{array}{rl}\hat{P}(C_1,x)=& \frac{5}{8}\times \frac{5}{12}\times \frac{7}{11}=0.16572\\ \hat{P}(C_2,x)=& \frac{3}{8}\times \frac{1}{8}\times \frac{3}{7}=0.02009\end{array}$$

  最终，通过概率模型来求类别：

$$\hat{y}=argma{x}_{k\in \{1,2\}}p(C_k)\prod _{i=1}^{2}p(x^{(i)}|C_k)=C_1$$

  因此，事件"x=(Outlook=Overcast,Windy=FALSE)"类别为“yes”。

代码：R language

用代码核算手算题

现在用代码来核算一下前面那个手算的例子。

数据准备

setwd("/Users/(你的用户名)/Documents/dataforexercise/data")
# 设定当前的工作目录，重要！
golf <- read.csv("golf.csv",header = T)
golf

训练集：只取Outlook和Windy这两个特征

train <- golf[,c(1,4,5)]
train

y_col <- 3 #因变量所在的列号
names(train)[y_col] <- 'y' #给因变量所在的列号命名为‘y’

测试集

testx <- data.frame(Outlook='Overcast',Windy='false')
levels(testx[,1]) <- levels(train[,1]) # 要求测试集中因子的水平与训练集一致
levels(testx[,2]) <- levels(train[,2])
testx

建模：NaiveBayes函数在klaR包里

if (!require(klaR)) {
    install.packages("klaR")
    library(klaR)
}

使用Laplace smoothing（NaiveBayes函数中参数fL=1）

NB.model <- NaiveBayes(y~.,data = train,fL = 1) #fL即贝叶斯估计中的lambda
NB.model

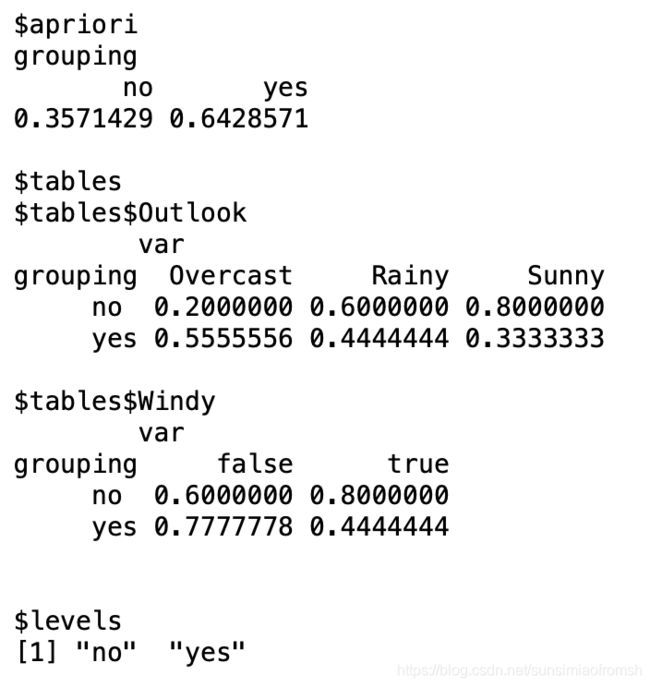
$apriori 显示y的各类别的先验概率

$tables 按y的类别分群体，显示各群体在每一个自变量（特征/属性）上的分布。由于这里的自变量都是定性的，因此是分别显示各取值所占比例。需要注意的是，R中自动按照字母顺序来排列各取值（从而，no就排在yes前面）。

请思考，如果自变量是定量数据，将如何描述这个分布？（要思考一下下嗷！后面有答案）

$levels 显示y的类别

预测：predict函数是系统自带的stat包里的

pred.NB <- predict(NB.model,testx)
pred.NB

$class 显示预测类别

$posterior 显示的预测为各类别的后验概率

klaR包中的NaiveBayes函数存在问题

这道题是前面那道手算题的代码，我们会发现，通过代码计算得的Laplace smoothing的贝叶斯先验/类条件概率的估计，和我们手算的结果都不同，且类条件概率不满足正则性（加起来总和0.2000000+0.6000000+0.8000000超过1）。

NB.model <- NaiveBayes(y~.,data = train,fL = 0) #fL=0，即 MLE
NB.model

我们可以发现，单纯利用MLE的结果是正确的，且Laplace smoothing的贝叶斯先验概率估计值和MLE先验估计值相同。

修正

我们尝试使用e1071::naiveBayes函数，能够解类条件概率不能正则化的问题，但是先验概率仍然为MLE（不管laplace等于几）

if (!require(e1071)) {
    install.packages("e1071")
    library(e1071)
}

e1071::naiveBayes函数使用方法：

NB.model.e1071 <- naiveBayes(y~.,data = train,laplace=1)
NB.model.e1071

例如，类别为“no”条件下Outlook取各值的条件概率之和0.1250000+0.3750000+0.5000000=1

pred.NB.e1071 <- predict(NB.model.e1701,testx)
pred.NB.e1071

预测类别为“yes”。

自变量是定性的问题

导入数据

setwd("/Users/(你的用户名)/Documents/dataforexercise/data")

computer <- read.csv("computer.csv",header = T)
computer

训练集和测试集划分

train <- computer
ycol <- 5
names(train)[ycol] <- 'y'

testx <- data.frame(age="youth",income="medium",student="yes",credit_rating="fair")
levels(testx[,1]) <- levels(train[,1]) # 要求测试集中因子的水平与训练集一致
levels(testx[,2]) <- levels(train[,2])
levels(testx[,3]) <- levels(train[,3])
levels(testx[,4]) <- levels(train[,4])
testx[1,1] <- "youth"
testx[1,2] <- "medium"
testx[1,3] <- "yes"
testx[1,4] <- "fair"
testx

建模：极大似然估计

if(!require(e1071)){
    install.packages('e1071')
    library(e1071)
}

NB.model <- naiveBayes(y~., train)  
NB.model

预测

pred.NB <- predict(NB.model,train[,-ycol])
pred.NB

评估

confusionMatrix函数在caret包中

if (!require(caret)) {
  install.packages("caret")
  library(caret)
}

eval.NB <- confusionMatrix(pred.NB,train[,ycol],positive = 'yes')
eval.NB

附一张来自R软件里的所有概念的计算图（具体含义以后会再开一个博文来讲）：

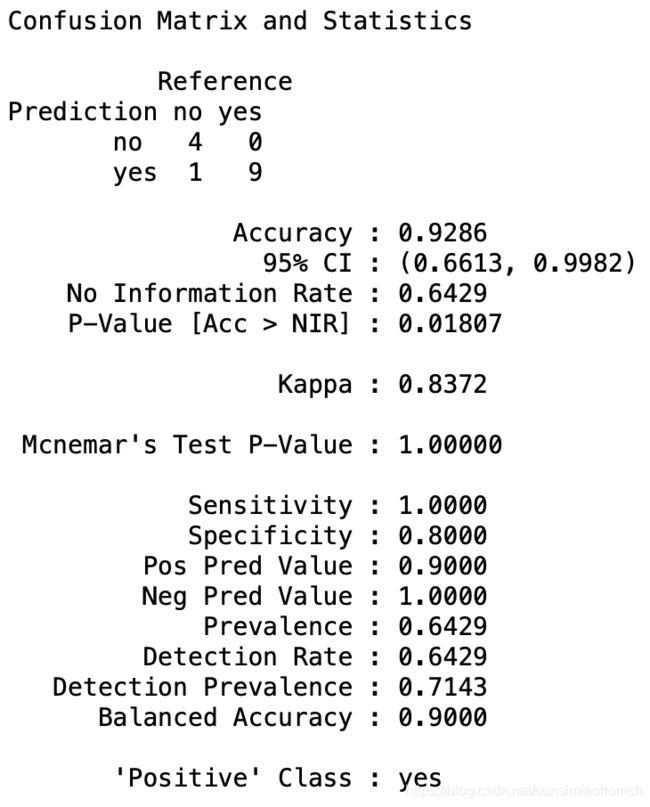
eval.NB$overall

Accuracy 0.928571428571429
Kappa 0.837209302325581
AccuracyLower 0.661315510068179
AccuracyUpper 0.998193219340875
AccuracyNull 0.642857142857143
AccuracyPValue 0.0180712092415321
McnemarPValue 1

eval.NB$byClass

Sensitivity 1
Specificity 0.8
Pos Pred Value 0.9
Neg Pred Value 1
Precision 0.9
Recall 1
F1 0.947368421052632
Prevalence 0.642857142857143
Detection Rate 0.642857142857143
Detection Prevalence 0.714285714285714
Balanced Accuracy 0.9

建模：Laplace smoothing的贝叶斯估计

NB.model.laplace <- naiveBayes(y~.,data = train,laplace = 1)
NB.model.laplace

预测

pred.NB.laplace <- predict(NB.model.laplace,train[,-ycol])
pred.NB.laplace

评估

eval.NB.laplace <- confusionMatrix(pred.NB.laplace,train[,ycol],positive = 'yes')
eval.NB.laplace

eval.NB.laplace$overall

Accuracy 0.928571428571429
Kappa 0.837209302325581
AccuracyLower 0.661315510068179
AccuracyUpper 0.998193219340875
AccuracyNull 0.642857142857143
AccuracyPValue 0.0180712092415321
McnemarPValue 1

eval.NB.laplace$byClass

Sensitivity 1
Specificity 0.8
Pos Pred Value 0.9
Neg Pred Value 1
Precision 0.9
Recall 1
F1 0.947368421052632
Prevalence 0.642857142857143
Detection Rate 0.642857142857143
Detection Prevalence 0.714285714285714
Balanced Accuracy 0.9

自变量是定量的问题

导入数据

setwd("/Users/(你的用户名)/Documents/dataforexercise/data")

golf <- read.csv("golf.csv",header = T)
golf

训练集和测试集的划分：只选择定量变量（此处不设训练集，比较训练集上预测结果和真实值的差异）

train <- golf
y_col <- 5
names(train)[y_col] <- 'y'

建模：高斯密度估计

if(!require(e1071)){
    install.packages('e1701')
    library(e1071)
}

NB.model <- naiveBayes(y ~ Temperature + Humidity, train)  
NB.model 

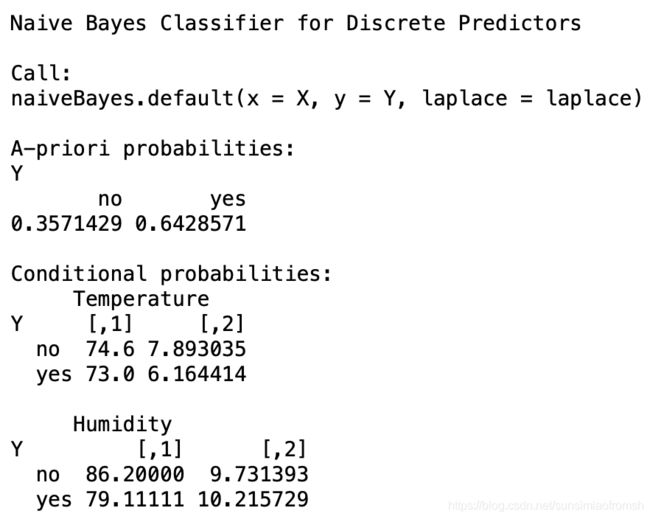
表格中给出的是Temperature和Humidity在各类下的均值和标准差：$tables中，[,1]是均值，[,2]是标准差（这就是上面思考题的答案！）

预测

pred.NB <- predict(NB.model,train[,2:3])
pred.NB

评估

方法一：gmodels包中的CrossTable函数

if(!require(gmodels)){
    install.packages('gmodels')
    library(gmodels)
}

CrossTable(train[,y_col], pred.NB,
           prop.chisq = FALSE, prop.t = FALSE, prop.r = FALSE,
           dnn = c('actual', 'predicted'))

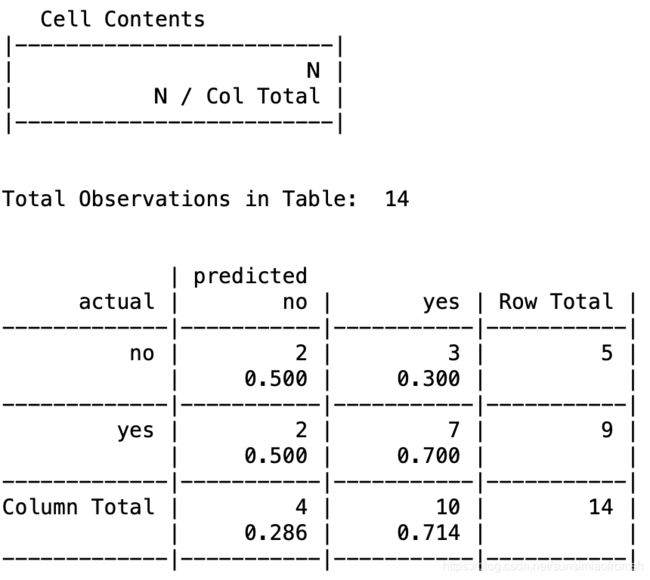
prop.r
如果为TRUE，输出结果则将包括行比例
prop.c
如果为TRUE，输出结果则将包括列比例
prop.t
如果为TRUE，输出结果则将包含表格比例
prop.chisq
如果为TRUE，输出结果则将包括每个单元的卡方贡献
上面四个值默认为TRUE

Cell Contents表示下面表格的单元格中，按顺序排下来分别是什么值。N代表同时满足行和列条件的个数，N/Col Total代表满足条件的个数在列中的占比。

方法二：table函数

table(train[,y_col],pred.NB)

对比一下klaR::NaiveBayes函数的功效

if (!require(klaR)) {
  install.packages("klaR")
  library(klaR)
}

NB.model.klaR <- NaiveBayes(y ~ Temperature + Humidity, train)  
NB.model.klaR

tables中给出的是Temperature和Humidity在各类下的均值和标准差：$tables中，[,1]是均值，[,2]是标准差。klaR包中的函数和e1071包中的函数作用效果相同。

建模：核密度估计

NB.model.kernel <- naiveBayes(y ~ Temperature + Humidity, train, usekernel = TRUE)  
NB.model.kernel 

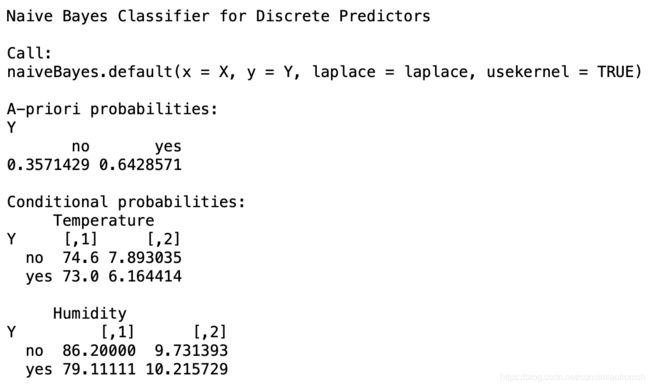
根据上图结果，e1071::naiveBayes函数不能实现核密度估计，只能进行高斯密度估计。

NB.model.kernel.klaR <- NaiveBayes(y ~ Temperature + Humidity, train, usekernel = TRUE)  
NB.model.kernel.klaR

tables中给出的是Temperature和Humidity在各类下的分位数值及其对应的密度值：以$tables$Temperature$no为例，其下方显示的是y=no的人群Temperature密度函数的描述，x那一列是y=no的人群Temperature的五数概括（最小值、下四分位数、中位数、上四分位数、最大值），y那一列是相应x处的密度函数值。

预测

pred.NB.kernel.klaR <- predict(NB.model.kernel.klaR,train[,2:3])
pred.NB.kernel.klaR

$class是预测类别，$posterior为预测为各个类别的概率，预测哪个类别的概率大，预测结果就为哪个类别。

评估

CrossTable(train[,y_col], pred.NB.kernel.klaR$class,
           prop.chisq = FALSE, prop.t = FALSE, prop.r = FALSE,
           dnn = c('actual', 'predicted'))

table(train[, y_col], pred.NB.kernel.klaR$class)

作图：密度函数

下面用plot函数画出不同变量的密度函数。

par(mfrow = c(1,2))
plot(NB.model.klaR,vars = 'Temperature')
# vars表明画哪个变量的密度函数，legendplot表示是否需要注释
# 高斯密度估计
plot(NB.model.kernel.klaR,vars = 'Temperature')
# 核密度估计
# 与直方图相似

par(mfrow = c(1,2))
plot(NB.model.klaR,vars = 'Humidity',legendplot = TRUE)
plot(NB.model.kernel.klaR,vars = 'Humidity',legendplot = TRUE)

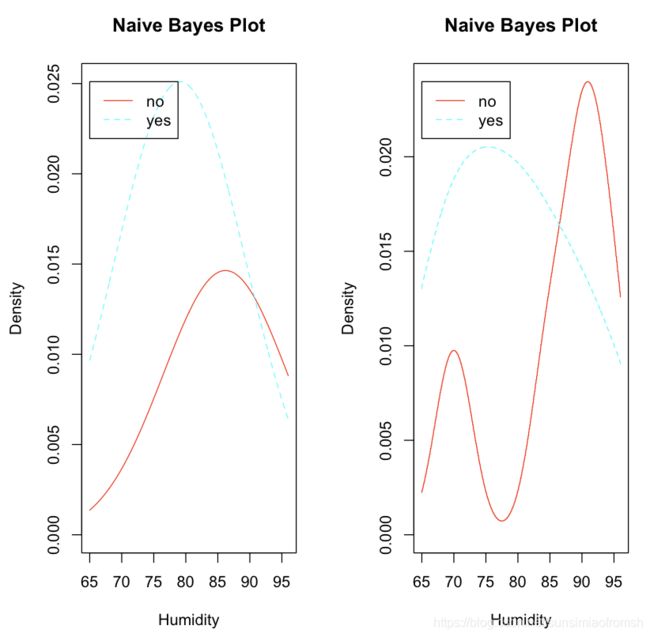
交叉验证

setwd("/Users/(你的用户名)/Documents/dataforexercise/data")
golf <- read.csv('golf.csv', header = T)

train <- golf
coly <- 5 # y所在的列号
names(train)[coly] <- "y"
train

留一交叉验证：只使用原本样本中的一项来当作验证集，而剩余的则留下来当作训练资料。这个步骤一直持续到每个样本都被当作一次验证集。

留一交叉验证可以用来寻找最优参数usekernel和fL的参数组合。

if (!require(klaR)) {
  install.packages("klaR")
  library(klaR)
}

usekernel = T和fL = 0的组合

pred.NB.list <- factor(rep("no", nrow(train)), level = c("no", "yes"))
for (i in 1 : nrow(train)){
  NB.model <- NaiveBayes(y ~., train[-i,], usekernel = T, fL = 0)  
  pred.NB <- predict(NB.model, train[i, -coly])
  pred.NB.list[i] <- pred.NB$class
}

下面使用caret包中的confusionMatrix函数，评价模型效果

if (!require(caret)) {
  install.packages("caret")
  library(caret)
}

eval.NB.cv <- confusionMatrix(pred.NB.list, train[, coly], positive = "yes")
eval.NB.cv

用留一交叉验证跑遍usekernel = T/F和fL = 0/1的四个组合，然后就能根据kappa值/准确率来选择最优参数组合。

代码：Python

用代码核算手算题&建模：多项式贝叶斯

下载所需包

import os # chdir函数
import pandas as pd #read_csv，iloc，DataFrame函数
import numpy as np # array，reshape函数
from sklearn.preprocessing import OneHotEncoder # 独热编码
from sklearn.naive_bayes import MultinomialNB # 多项式朴素贝叶斯

改变路径

os.chdir函数用于改变当前工作目录到指定的路径；由于’‘有转义作用，r''表示’'内部的字符串默认不转义(仅输入原始字符串，常用于路径输入)

os.chdir(r"/Users/(你的用户名)/Documents/dataforexercise/data")

导入数据

pandas.read_csv函数用于读取 ‘.csv’ 文件，常用参数如下：

header：设置导入 DataFrame 的列名称，默认为 infer，注意它与下面介绍的names参数的微妙关系。

names：当names没被赋值时，header会变成第0行的内容，即选取数据文件的第一行作为列名；当 names 被赋值，header 没被赋值时，那么原来的header就会变成数据的第0行，列名会变成names；如果都赋值，就会实现两个参数的组合功能，即将 names 的值作为列名。

index_col：我们在读取文件之后，生成的索引默认是0 1 2 3…，可以set_index，但也可以在读取的时候就指定某个列为索引，index_col 就是用来指定某个列作为索引，index_col的值可以取列名。

dtype：可用通过dtype={"列名": 数据类型}来定义数据类型。

converters：可以在读取的时候对列数据进行变换，例如converters={"列名": lambda x: int(x) + 10}那该列所有数字会+10.

nrows：设置一次性读入的文件行数，它在读入大文件时很有用。

na_values：可以配置哪些值需要处理成 NaN，na_values={“name”: ["#"], “gender”: [“女”]}代表name列中的#作为缺失值，gender列中的女作为缺失值。

golf = pd.read_csv('golf.csv')
golf

划分训练集和测试集

首先，挑出我们要用的Outlook、Windy和因变量的列，构成我们用的usedata.

usedata = golf.iloc[0:,[0,3,4]]
usedata

训练集

x_train = usedata.iloc[0:,[0,1]]
y_train = usedata.iloc[0:,2]
x_train,y_train

测试集

pd.DataFrame函数可以创建DataFrame类型的数据集，构建它的方法有很多，最常见的一种就是传入一个由等长列表或numpy数组组成的字典，例如

data = {'STATE':['OHIO','NEVADA'],
        'YEAR':[2001,2002]}
frame = DataFrame(data)

reshape函数中的参数就是张量的形状，’-1’就是不考虑那个行/列数，端看其他一个列/行是多少，再把数据总量除以这个数，得到’-1’对应的行/列数。

x_test = pd.DataFrame(['Overcast', False])
x_test = np.array(x_test).reshape((1,-1))
x_test

独热编码

由于自变量是定性变量，所以考虑多项式朴素贝叶斯MultinomialNB，测试发现MultinomialNB不能直接处理定性数据，需做独热编码。

encoder.fit_transform(x_train)先将独热编码取1的矩阵（行号，列号）标记下来，再用toarray函数将之转化为独热编码矩阵。

encoder = OneHotEncoder() # 给独热编码函数重命名
x_train_onehot = pd.DataFrame(encoder.fit_transform(x_train).toarray())
x_train_onehot

x_test_onehot = encoder.transform(x_test)
x_test_onehot

建模：多项式贝叶斯

适合自变量离散的场合，MultinomialNB函数中alpha参数就是lambda，alpha = 1即拉普拉斯光滑。

MultinomialNB.fit(X,y)函数建模函数，X训练集自变量，y训练集因变量，sample_weight加权值。

mnb = MultinomialNB(alpha = 1)
MNBmodel = mnb.fit(x_train_onehot, y_train)

预测

预测类别

MNBmodel.predict(x_test_onehot)

预测类别概率

MNBmodel.predict_proba(x_test_onehot)

解释一下这个概率的由来：先验概率用的是MLE，类条件概率用的是laplace光滑的贝叶斯估计，计算出来预测类别为’no’的概率为0.0191326531，'yes’的概率为0.170454545，MultinomialNB.predict_proba函数会有将概率归一化这一步骤，预测类别为’no’的概率为$\frac{0.0191326531}{0.0191326531+0.170454545}=0.10068519$，'yes’的概率为$\frac{0.170454545}{0.0191326531+0.170454545}=0.89931481$。

Python中的朴素贝叶斯的laplce光滑是正确的。

建模：高斯贝叶斯

下载所需包

import os # chdir函数
import pandas as pd #read_csv，iloc，DataFrame函数
import numpy as np # array，reshape函数
from sklearn.preprocessing import OneHotEncoder # 独热编码
from sklearn.naive_bayes import GaussianNB # 多项式朴素贝叶斯

划分训练集和测试集

使用数据集

usedata = golf.iloc[0:,[1,2,4]]
usedata

训练集

x_train = usedata.iloc[0:,[0,1]]
y_train = usedata.iloc[0:,2]
x_train,y_train

测试集

x_test = pd.DataFrame([85, 85])
x_test = np.array(x_test).reshape((1,-1))
x_test

建模：高斯贝叶斯

gnb = GaussianNB()
GNBmodel = gnb.fit(x_train,y_train)

预测

GNBmodel.predict(x_test)

GNBmodel.predict_proba(x_test)

预测类别为’no’的概率为0.63248179, 预测类别为’yes’的概率为0.36751821。

建模：混合型自变量

下载所需包

import os # chdir函数
import pandas as pd #read_csv，iloc，DataFrame函数
import numpy as np # array，reshape函数
from sklearn.preprocessing import OneHotEncoder # 独热编码
from sklearn.naive_bayes import MultinomialNB,GaussianNB # 多项式朴素贝叶斯和朴素贝叶斯

改变路径

os.chdir(r'/Users/sunsimiao/Documents/dataforexercise/data/')

划分训练集和测试集

选择使用数据

golf = pd.read_csv('golf.csv')
golf

训练集：划分为定性变量训练集，定量变量训练集

x_train1 = golf.iloc[0:,[0,3]]
y_train1 = golf.iloc[0:,4]

x_train2 = golf.iloc[0:,[1,2]]
y_train2 = golf.iloc[0:,4]

测试集：划分为定性变量测试集，定量变量测试集

x_test1 = pd.DataFrame(['Overcast',False])
x_test1 = np.array(x_test1).reshape((1,-1))

x_test2 = pd.DataFrame([85, 85])
x_test2 = np.array(x_test2).reshape((1,-1))

下面对MultinomialNB和GaussianNB进行整合，只要把其中一个模型的各类先验概率设置为等概率，然后把两个模型的概率值相乘即可。

独热编码

encoder = OneHotEncoder()
x_train1_onehot = pd.DataFrame(encoder.fit_transform(x_train1).toarray())

x_test1_onehot = encoder.transform(x_test1)

建模

mnb = MultinomialNB(alpha=1)
MNBmodel = mnb.fit(x_train1_onehot,y_train1)

gnb = GaussianNB(priors=[0.5,0.5]) # 把其中一个模型的各类先验概率设置为等概率
GNBmodel = gnb.fit(x_train2,y_train2)

预测

MNBpred = MNBmodel.predict_proba(x_test1_onehot)

GNBpred = GNBmodel.predict_proba(x_test2)

ypred = MNBpred * GNBpred # 把两个模型的概率值相乘
ypred/ypred.sum()

结果：

array([[0.25750649, 0.74249351]])

说明&致谢

  深深地怀疑朴素贝叶斯(Naïve Bayes)中的这个’Naive’是在吐槽这个算法太“天真”地假设类别之间的独立性，博主脑洞：那为什么不叫天真贝叶斯呢？

  阅读至此的一定是好学的小哥哥小姐姐啦！一起加油学机器学习咯，欢迎也感谢各位小哥哥小姐姐到评论区指出文中问题。在此，特要感谢本人机器学习的授课老师Ms.L（貌美如花的实力派老师）提供的资料和教学。Come and Join Us Machine Learning！

  接下来，博主计划分享KNN学习的读书笔记。

参考资料

---

1. 李航. 统计学习方法, 2015, 清华大学出版社 ↩︎

2. The Elements of Statistical Learning ↩︎