几种最短路径算的Python实现
最近学习了一些关于最短路径算法的知识,感觉很有意思,但是网路上很多的算法斗志又C或C++的实现方式,很少有Python。于是我就想来自己些个Python最短路径的教程,权当复习自己的知识。
最短路径算法是图类问题中一个经典问题,旨在寻找又节点和边构成的图中任意一点到任意一点的最短路径。今天我要介绍的主要是Floyd-Warshall算法,Dijkstra算法和Bellman-Ford。算法。
第一个介绍的是Floyd-Warshall算法
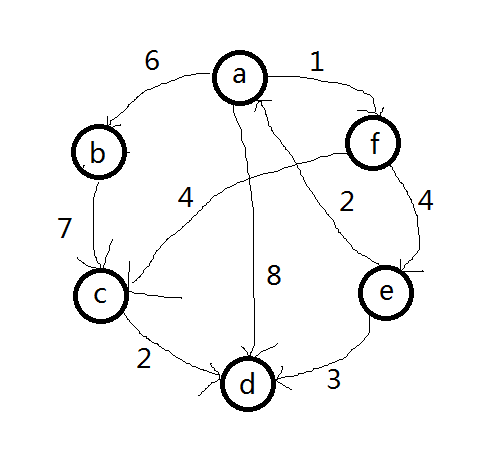
在这个图中,字母表示顶点,数字表示每个定点之间的距离。假如我们现在要找出从A点到D点的的短路径怎么办?你当然可以把每条路径的距离都算出来,一一比较,像这样。
A - D : 8
A - F - E - D : 8
A - B - C - D : 15
A - F - C - D : 7
最后发现最短的路径是A - F - C - D,这个问题之所以能够这样解决,是因为我们的图不复杂,可以使用穷举的方法找出所有的可能。但是,如果说我们面对的是一个有500定点的图,那我们要怎么穷举呢?这个时候我们就需要金光闪闪的Flolyd-Warshall算法来帮助我们啦。
不过再具体学习算法之前我们需要建立一个表格来保存图。X表示两个点之间不能直接到达
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | X | X | 1 |
| B | X | X | 7 | X | X | X |
| C | X | X | X | 2 | x | X |
| D | X | X | X | X | X | X |
| E | 2 | X | X | 3 | X | X |
| F | X | X | 4 | X | 4 | X |
得到这一个表格后,我们就可以很轻松的将这个表转换为二位数组啦~
TaDa~现在真正要来介绍Floyd-Warshall算法啦!其实Floyed算法很简单:
”如果说两个点之间的直接路径不是最短路径的话,必然有一个或者多个点供中转,使其路径最短。“
那如何用计算机语言来描述这个算法呢?
for i in range(len(vertex)):
for j in range(len(dis)):
for k in range(len(dis[j])):
if dis[i][j] > dis[i][k]+dis[k][j]:
dis[i][j] = dis[i][k]+dis[k][j]第一个循环和第二个循环的用途很明显,用来定位二维数组的值,按下不表。
第三个循环就是用来寻找供中转的点了,需要特别注意,最开始学习这个算法的时候我认为这个算法只能找到一个点作为中转,不能提供多个点供中转,后面仔细一看发现我的理解是错误的。
现在假设我们有这样一个中转方案
dis = [
[ 999 , 2, 999 , 999 , 2 , 10 ],
[ 999 , 999 , 999 , 999 , 999 , 6,],
[ 999 , 999 , 999 , 999 , 999 , 1 ],
[999 , 999 , 999 , 999 , 999 , 999 ],
[ 999, 999 ,1 ,999 , 999 , 999 ],
[ 999 ,999 ,999 , 999 , 999 ,999 ],
]
A - F : 10
A - B - F : 8
A - E - C - F : 6
我们可以直观的发现1,从点A - 点F的最短距离是通过 E C 者两个点近行中转,那这个中转在算法中是如何实现的呢?
首先,计算机在找从A - C点的最短路径时发现,[A][C]>[A][E]+[E][C]
着时,将A - C 的距离替换位 A - E -C ,这就意味着在后面所有由A点出发,C点中转的点都变成从A点出发,经过E C两个点转。
然后计算机再找从A - F的,也会依次将 A - F之间所有的点都作为中转点一一尝试,但是在试到 A - C - F这个点时,由于 A - C的距离已经被更短的 A - E - C替换,友谊 A - C - F 实际上走的是 A - E - C - 这条路径。
Floyd-Warshall算法需要执行三次for循环,故其时间复杂度为O(N^3)。
Dijkstra 算法
Floyd-Warshall算法虽然好,但是每次计算都会将所有的的点之间的最短路径计算出来,可是有的时候,我们也许只需要一个点到其他点之间的最短路径,并不需要其他点之间的最短路径。这时怎么办呢?Dijkstra 算法这时就派上用场啦。
Dijkstra算法 通过一种‘松弛’的思想来得出一个点到另一个点的最短路径,具体怎么算的呢,我们先来看一个例子,X表示距离无穷远:
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | 4 | X | 1 |
| B | 5 | X | 7 | 7 | X | X |
| C | X | X | X | 2 | 4 | X |
| D | X | 3 | 5 | X | 1 | 7 |
| E | 2 | X | X | 3 | X | X |
| F | X | 3 | 4 | X | 4 | X |
然后,我们新建一个列表来表示A点到其他点的距离
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | 4 | X | 1 |
如果两个部分的距离之和为最小值,那这两个部分也应当为最小值,这就是Dijkstra 算法的中心思想。观察A 到其他点的距离,我们发现从A 点
到F点的直线距离最小,这时,我们称从A 点 到 F点的这个距离为确定距离,然后使用F点来松弛其他的边。
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | x | 5 | 1 |
这时我们发现,通过F点进行中转可以有效的简单,A - B, A - C,A - E的值,然后现仔,我们在从A 到 除 F而外的所有点中,找出距离最小的点,最为确定值,进行下一一次松弛。 然后我们发现,A - B 点的距离目前最短,所以再用B点进行一次松弛。
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 11 | 5 | 1 |
现在我们得到了由B点进行松弛过后的结果,现在再来继续寻找除 B,F意外距离A点最近的点,然后我们发现C 点和E 点都是5,那我们就现在用C点进行松弛
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
然后我们发现 经过 C点松弛, A - D的距离可以变短,现在,我们是用E点进行松弛
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
没有什么变化,现在在使用最后的D点进行松弛,由于D点是最后一个点,一般来说当使用最后一个点进行松弛时,最短路径其实已经找了出来。所以A 到其他各个定点的最短路径为
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
那现在,这个算法要怎么使用Python描述出来呢?
nodes = ('A', 'B', 'C', 'D', 'E', 'F', 'G')
distances = {
'B': {'A': 5, 'D': 1, 'G': 2},
'A': {'B': 5, 'D': 3, 'E': 12, 'F' :5},
'D': {'B': 1, 'G': 1, 'E': 1, 'A': 3},
'G': {'B': 2, 'D': 1, 'C': 2},
'C': {'G': 2, 'E': 1, 'F': 16},
'E': {'A': 12, 'D': 1, 'C': 1, 'F': 2},
'F': {'A': 5, 'E': 2, 'C': 16}}
unvisited = {node: None for node in nodes} #把None作为无穷大使用
visited = {}#用来记录已经松弛过的数组
current = 'B' #要找B点到其他点的距离
currentDistance = 0
unvisited[current] = currentDistance#B到B的距离记为0
while True:
for neighbour, distance in distances[current].items():
if neighbour not in unvisited: continue#被访问过了,跳出本次循环
newDistance = currentDistance + distance#新的距离
if unvisited[neighbour] is None or unvisited[neighbour] > newDistance:#如果两个点之间的距离之前是无穷大或者新距离小于原来的距离
unvisited[neighbour] = newDistance#更新距离
visited[current] = currentDistance#这个点已经松弛过,记录
del unvisited[current]#从未访问过的字典中将这个点删除
if not unvisited: break#如果所有点都松弛过,跳出此次循环
candidates = [node for node in unvisited.items() if node[1]]#找出目前还有拿些点未松弛过
current, currentDistance = sorted(candidates, key = lambda x: x[1])[0]#找出目前可以用来松弛的点
这段代码的第一次循环不会用任何点进行松弛,第一次循环的主要目的在于将目前到各个点的距离排个序,找出下一次用来松弛的点。这个算法的时间复杂度只有O(N^2)。如果具备堆的知识,还可以顺利的把这个算法的时间复杂度降到O(M+N)LogN。但是,这回算法依然不能解决带负权的图,那我们遇到带负权的图又该怎么办呢?这时我们就需要Bellman-Ford算法啦!
Bellman-Ford算法
Bellman-Ford算法可以非常好的解决带有负权的最短路径问题,什么是负权?如果两个顶点之间的距离为正数,那这个距离成为正权。反之,如果一个顶点到一个顶点的距离为负数,那这个距离就称为负权。Bellman-Ford和Dijkstra 相似,都是采用‘松弛’的方法来寻找最短的距离。现在,我们来看看Bellman-Ford的例子。
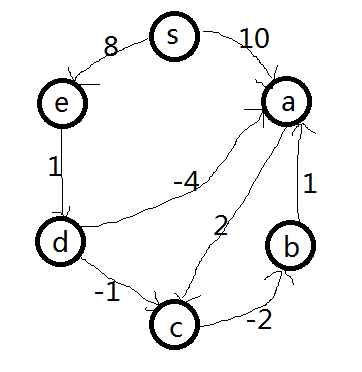
Bellman-Ford是如何找到从S点到其他点的最短距离的呢?
初始状态:
| s: | a: | b: | c: | d: | e: |
|---|
第一次松弛我们发现,S点可以直接到达e点和a点,然后通过e点和a点可以到达d,c,,然后通过c点可以到达b,现在更新我们的表格
| s: | a:10 | b:10 | c:12 | d:9 | e:8 |
|---|
当所有点都松弛过一次后,我们进行第二次松弛,在进行第二次松弛的时候,我会可以发现d到啊a,c都是负权,应该可以减少距离。
| s: | a:5 | b:10 | c:8 | d:9 | e:8 |
|---|
这时第二次松弛的结果,现在我们要进行第三次次松弛
| s: | a:5 | b:5 | c:7 | d:9 | e:8 |
|---|
好了现在我们要开始第四次松弛了,所以到底我们需要几次松弛呢。请偶们需要顶点数减一次松弛,因为在图中,任意两点的最短路径至多包含N-1条边,如果经过N-1次松弛以后还能继续松弛,则说明这个图是一个有负权回路的图,没有最短路径。
第四次松弛:
| s: | a:5 | b:5 | c:7 | d:9 | e:8 |
|---|
第四次松弛与第三次松弛结果一直,这说明我们现在已经找到从S点到图中其他的最短路径。
关门!上代码!
G = {1:{1:0, 2:-3, 5:5},
2:{2:0, 3:2},
3:{3:0, 4:3},
4:{4:0, 5:2},
5:{5:0}}
def getEdges(G):
""" 读入图G,返回其边与端点的列表 """
v1 = [] # 出发点
v2 = [] # 对应的相邻到达点
w = [] # 顶点v1到顶点v2的边的权值
for i in G:
for j in G[i]:
if G[i][j] != 0:
w.append(G[i][j])
v1.append(i)
v2.append(j)
return v1,v2,w
def Bellman_Ford(G, v0, INF=999):
v1,v2,w = getEdges(G)
# 初始化源点与所有点之间的最短距离
dis = dict((k,INF) for k in G.keys())
dis[v0] = 0
# 核心算法
for k in range(len(G)-1): # 循环 n-1轮
check = 0 # 用于标记本轮松弛中dis是否发生更新
for i in range(len(w)): # 对每条边进行一次松弛操作
if dis[v1[i]] + w[i] < dis[v2[i]]:
dis[v2[i]] = dis[v1[i]] + w[i]
check = 1
if check == 0: break
# 检测负权回路
# 如果在 n-1 次松弛之后,最短路径依然发生变化,则该图必然存在负权回路
flag = 0
for i in range(len(w)): # 对每条边再尝试进行一次松弛操作
if dis[v1[i]] + w[i] < dis[v2[i]]:
flag = 1
break
if flag == 1:
# raise CycleError()
return False
return dis
v0 = 1
dis = Bellman_Ford(G, v0)
print dis.values()Bellman-Ford算法的时间复杂度是O(MN),但是我们依然可以对这个算法进行优化,在实际使用中,我们常常会发现不用循环到N-1次就能求出最短路径,所以我们可以比较前后两次松弛结果,若果两次结果都一致,可说明松弛完成,不用再继续循环了。
Bellman-Ford与Dijkstra的区别
Bellman-Ford可以用于含有负权的图中而Dijkstra不可以。
为什么Dijkstra不可以?其跟本的原因在于,在Dijkstra,一旦一个顶点用来松弛过以后,其最小值已经固定不会再参与到下一次的松弛中。因为Dijkstra中全部的距离都是正权,所以不可能出现A - B - C 之间的距离比 A - B - D - C 的距离短的情况,而Bellman-Ford则在每次循环中,则会将每个点都重新松弛一遍,所以可以处理负权。
暂时就想到这一点的区别,想起来再补充咯,啾咪~