谈多模匹配算法-AC状态机
谈一下基于trie树的AC匹配算法。
trie树,又称单词查找树、字典树,是一种树形结构,是一种哈希树的变种,是一种用于快速检索的多叉树结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
AC匹配算法,由关键字组成的集合构成一个有限状态机,将要匹配的text作为输入(触发),输出命中哪些关键字。
trie树
以{he, she, his, hers, isher}的顺序插入,形成trie树。
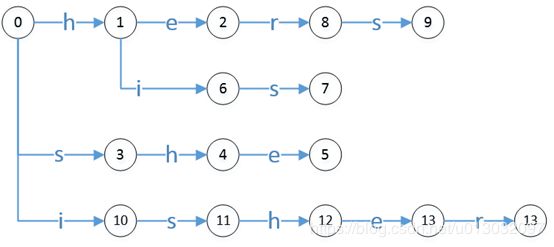
AC匹配算法
AC匹配算法,在trie树的基础上,增加了失败跳转函数和输出函数,以形成状态机。
跳转函数g(s,t)的构造
其中参数s为状态,t为触发,如上图,有g(0,h) = 1, g(1,i) = 2。
失败跳转函数f(s)的构造
这是AC匹配算法的关键,首先对depth为1的状态s,有f(s)=0;之后,递归的所有depth为d的状态,其失败跳转函数f(s)都依赖于depth为d-1的失败跳转函数。
如何依赖depth为d-1的失败跳转函数?
设depth为d的状态为s,d-1的状态为r,触发字符为a。如果state = f(r),若g(state, a) != fail,则f(s) = g(state, a);若g(state, a) = fail,执行若干次state = f(state),直至g(state, a) != fail, f(s) = g(state, a)。
即:
state = f(r )
while(g(state, a) == FAIL) {
state = f(state);
}
f(s) = g(state, a);
以图1-1为例说明这个过程,首先,将状态1,3,10的失败跳转指向状态0,然后考虑depth为2的结点2,6,4,11:
计算f(2)时候,我们设置state=f(1)=0,因为g(0,e)=0,所以f(2)=0;
计算f(6)时候,我们设置state=f(1)=0,因为g(0,i)=0,所以f(6)=0;
计算f(4)时候,我们设置state=f(3)=0,因为g(0,h)=1,所以f(4)=1;
计算f(11)时候,我们设置state=f(10)=0,因为g(0,s)=3,所以f(11)=3;
然后考虑depth为3的节点8,7,5,12:
计算f(8)时候,我们设置state=f(2)=0,因为g(0,r)=0,所以f(8)=0;
计算f(7)时候,我们设置state=f(6)=0,因为g(0,s)=3,所以f(7)=3;
计算f(5)时候,我们设置state=f(4)=1,因为g(1,e)=2,所以f(5)=2;
计算f(12)时候,我们设置state=f(11)=3,因为g(3,h)=4,所以f(12)=4;
然后考虑depth为4的节点9,13:
计算f(9)时候,我们设置state=f(8)=0,因为g(0,s)=3,所以f(9)=3;
计算f(13)时候,我们设置state=f(12)=4,因为g(4,e)=5,所以f(13)=5;
然后考虑depth为5的节点14:
计算f(14)的时候,我们设置state=f(13)=5,因为g(5,r)=fail,所以state=f(5)=2,因为g(2,r)=8,所以f(14)=8。
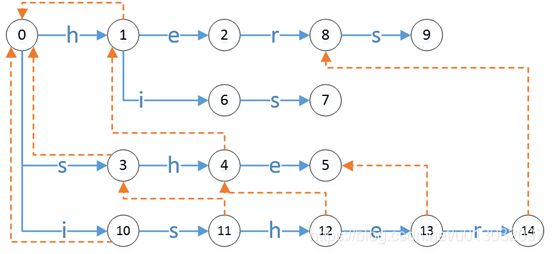
因为深度为1的状态失败跳转态为0,因为我们采用递归的方式计算后面状态的失败跳转状态,所以后面所有状态都可以计算出失败跳转,即最差也会跳转至0。
另外,某状态的失败跳转态,总是跳至该状态下最长匹配态。如图,状态13即“ishe”,它及包含“he”(状态2),也包含“she”(状态5),但13的失败跳转态是5,因为“she”是“ishe”的最长匹配,这是由上述算法决定的结论,不再细究。
输出的构造
在形成trie树过程中,需要在某些状态形成输出,如在状态2输出“he”,在状态5输出“she”,在一个状态只是单输出。但AC匹配算法存在多输出情况,即在状态5,既匹配上“she”,实际也匹配上了“he”,那么在状态5就应该保存“she”和“he”两个输出。
AC匹配算法的输出是在失败跳转的构造过程中构造,在计算出状态5的失败跳转态是2时,同时也将2的输出添加至状态5,这样状态5就有“she”和“he”两个输出。
同样的,在计算出状态13的失败跳转是5后,也将状态5的输出添加至状态13,这样一步步递归,后面的状态总是包含它能匹配上前面状态的输出。
时间复杂度
匹配过程中,查找的时间复杂度和预先输入的关键字数量及长度无关,只和要匹配的输入字符串长度有关,对于规模为N的输入,其时间复杂度为O(N)。