深度学习框架tensorflow实战(实现线性回归算法)
首先制造一个分布在某直线的数据集
我们围绕着目标y1=x1*0.1+0.3来建立
非常简单的得到,利用随机函数
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
num_points = 1000
vectors_set = []
for i in range(num_points):
x1=np.random.normal(0.0,0.55)
y1=x1*0.1+0.3+np.random.normal(0.0,0.03) #加上一些随机项
vectors_set.append([x1,y1])
x_data = [v[0]for v in vectors_set]
y_data = [v[1] for v in vectors_set]
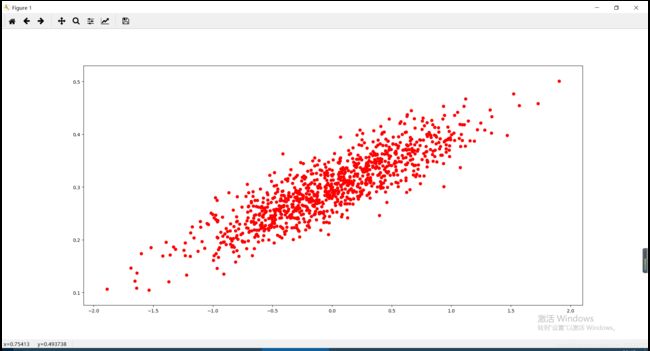
plt.scatter(x_data,y_data,c='r')
plt.show()
效果图:
我们的目标去求w,b
我们先将w和b进行随机初始化,然后我们会有个预测值,我们基于最小二乘法,利用梯度下降减少损失,越少的损失对应的w和b就是我们想要获得的结果。
其实这个线性回归之前已经利用过matlab去实现过了,但我们现在要用tensorflow去实现~
#生成1维的W矩阵,取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1],-1.0,1.0),name='W')
#生成1维的b矩阵,初始值是0
b = tf.Variable(tf.zeros([1]))
#经过计算得到预测值y
y = W * x_data + b
#计算误差
loss= tf.reduce_mean(tf.square(y-y_data))
#梯度下降优化器,0.5为学习率
optimizer = tf.train.GradientDescentOptimizer(0.5)
#训练的过程就是最小化这个误差值
train = optimizer.minimize(loss)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))
#执行20次训练
for step in range(20):
sess.run(train) #包含训练中所有的了
print("W=", sess.run(W), "b=", sess.run(b), "loss=", sess.run(loss))
结果图:
W= [-0.17971134] b= [0.] loss= 0.114719525
W= [-0.09490481] b= [0.30004138] loss= 0.0125605455
W= [-0.03599591] b= [0.29986188] loss= 0.006653693
W= [0.00536524] b= [0.29973722] loss= 0.0037417721
W= [0.03440576] b= [0.2996497] loss= 0.0023062723
W= [0.05479571] b= [0.29958823] loss= 0.0015986093
W= [0.06911192] b= [0.29954508] loss= 0.0012497499
W= [0.07916363] b= [0.29951477] loss= 0.0010777717
W= [0.08622113] b= [0.2994935] loss= 0.0009929909
W= [0.09117635] b= [0.29947856] loss= 0.0009511963
W= [0.09465551] b= [0.29946807] loss= 0.0009305927
W= [0.09709831] b= [0.2994607] loss= 0.00092043565
W= [0.09881344] b= [0.29945555] loss= 0.0009154285
W= [0.10001767] b= [0.29945192] loss= 0.00091296004
W= [0.10086319] b= [0.29944938] loss= 0.0009117433
W= [0.10145684] b= [0.29944757] loss= 0.00091114343
W= [0.10187366] b= [0.2994463] loss= 0.0009108476
W= [0.10216632] b= [0.29944545] loss= 0.0009107019
W= [0.1023718] b= [0.29944482] loss= 0.00091063
W= [0.10251607] b= [0.29944438] loss= 0.0009105946
W= [0.10261737] b= [0.29944408] loss= 0.00091057713
可以看到w越来越接近0.1,b越来越接近0.3,loss越来越小,迭代20次的模型就达到这个比较不错的效果了~
完整代码:
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
num_points = 1000
vectors_set = []
for i in range(num_points):
x1=np.random.normal(0.0,0.55)
y1=x1*0.1+0.3+np.random.normal(0.0,0.03) #加上一些随机项
vectors_set.append([x1,y1])
x_data = [v[0]for v in vectors_set]
y_data = [v[1] for v in vectors_set]
#生成1维的W矩阵,取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1],-1.0,1.0),name='W')
#生成1维的b矩阵,初始值是0
b = tf.Variable(tf.zeros([1]))
#经过计算得到预测值y
y = W * x_data + b
#计算误差
loss= tf.reduce_mean(tf.square(y-y_data))
#梯度下降优化器,0.5为学习率
optimizer = tf.train.GradientDescentOptimizer(0.5)
#训练的过程就是最小化这个误差值
train = optimizer.minimize(loss)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))
#执行20次训练
for step in range(20):
sess.run(train) #包含训练中所有的了
print("W=", sess.run(W), "b=", sess.run(b), "loss=", sess.run(loss))
plt.scatter(x_data,y_data,c='r')
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()