决策树(一):初步学习
决策树初步接触
- 介绍
- 背景引入
- 优缺点、适用数据类型
- 伪代码引入
- 决策树的一般流程
- 案例引入
- 信息增益
- 熵
- 划分数据集
- 递归构建决策树
- 总结
介绍
决策树
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
分类树(决策树)是一种十分常用的分类方法。他是一种监管学习,所谓监管学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。
背景引入
图 3-1构 造 了 一 个 假 想 的 邮 件 分 类 系 统 ,它 首 先 检 测 发 送 邮 件 域 名 地 址 。如果地址为 myEmpIoyer.com,则将其放在分类“ 无聊时需要阅读的邮件”中。如果邮件不是来自这个域名, 则检查邮件内容里是否包含单词曲棍球,如果包含则将邮件归类到“ 需要及时处理的朋友邮件” , 如果不包含则将邮件归类到“无需阅读的垃圾邮件” 。
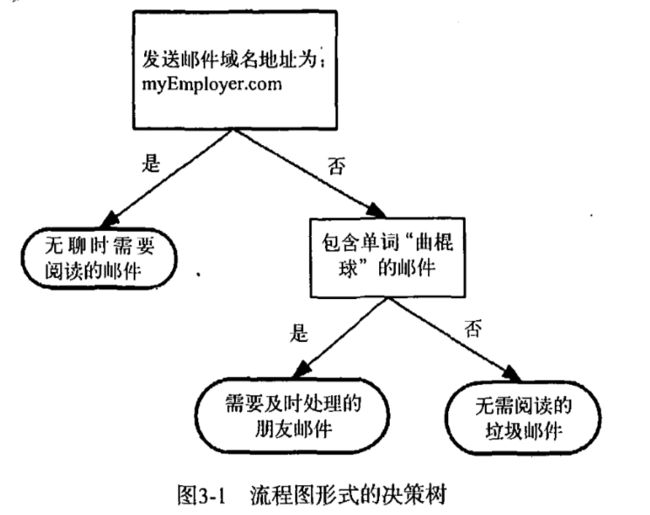
决策树就是这么容易理解。
优缺点、适用数据类型
-
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
-
缺点:可能会产生过度匹配问题。
-
适用数据类型:数值型和标称型。
伪代码引入
在构造决策树时,我们需要解决的第一个问题就是,当前数据集上哪个特征在划分数据分类时起决定性作用。为了找到决定性的特征,划分出最好的结果,我们必须评估每个特征。完成测试之后,原始数据集就被划分为几个数据子集。这些数据子集会分布在第一个决策点的所有分支上。如果某个分支下的数据属于同一类型,则当前无需阅读的垃圾邮件已经正确地划分数据分类,无需进一步对数据集进行分割。如果数据子集内的数据不属于同一类型,则需要重复划分数据子 的过程。如何划分数据子集的算法和划分原始数据集的方法相同,直到所有具有相同类型的数据均在一个数据子集内。
If so return 类标签:
Else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数createBranch()并增加返回结果到分支节点中
return 分支节点
上面的伪代码是一个递归函数,在倒数第二行直接调用了它自己。后面我们将把上面的伪代码转换为python代码,这里我们需要进一步了解算法是如何划分数据集的。
决策树的一般流程
使用决策树做预测需要以下过程:
收集数据:可以使用任何方法。比如想构建一个相亲系统,我们可以从媒婆那里,或者通过参访相亲对象获取数据。根据他们考虑的因素和最终的选择结果,就可以得到一些供我们利用的数据了。
准备数据:收集完的数据,我们要进行整理,将这些所有收集的信息按照一定规则整理出来,并排版,方便我们进行后续处理。
分析数据:可以使用任何方法,决策树构造完成之后,我们可以检查决策树图形是否符合预期。
训练算法:这个过程也就是构造决策树,同样也可以说是决策树学习,就是构造一个决策树的数据结构。
测试算法:使用经验树计算错误率。当错误率达到了可接收范围,这个决策树就可以投放使用了。
使用算法:此步骤可以使用适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
本节使用ID3算法来划分数据集,该算法处理如何划分数据集,何时停止划分数据集。
案例引入
表3-1的数据包含5个海洋动物,特征包括:不浮出水面是否可以生存,以及是否有脚蹼。我 们可以将这些动物分成两类:鱼类和非鱼类。现在我们想要决定依据第一个特征还是第二个特征 划分数据。在回答这个问题之前,我们必须采用量化的方法判断如何划分数据。

信息增益
划分数据集的大原则是:将无序数据变得更加有序,但是各种方法都有各自的优缺点,信息论是量化处理信息的分支科学,在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择,所以必须先学习如何计算信息增益,集合信息的度量方式称为香农熵,或者简称熵.
什么是信息增益呢?在划分数据集之前之后信息发生的变化成为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
熵
熵定义为信息的期望值,如果待分类的事物可能划分在多个类之中,则符号Xi的信息定义为:

为了计算熵,我们需要计算所有类别所有可能值所包含的信息期望值,通过下式得到:

其中,n为分类数目,熵越大,随机变量的不确定性就越大,就越不纯。
下面我们将学习如何使用python计算信息熵
# 计算数据集的香农熵
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: # 为所有可能分类创建字典
currentLabel = featVec[-1] # 取数据集的标签
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0 # 分类标签值初始化
labelCounts[currentLabel] += 1 # 给标签赋值
shannonEnt = 0.0 # 熵初始化
for key in labelCounts:
prob = float(labelCounts[key])/numEntries # 求得每个标签的概率 # L(Xi) = -log2P(Xi)
shannonEnt -= prob * log(prob, 2) # 以2为底求对数 # H = - Σi=1 n P(Xi)*log2P(Xi)
# 注意这里是-= 虽然是求和 但是求和值<0 所以这里-=
return shannonEnt
# 创建简易鉴定鱼数据集
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
# [是否可以浮出水面,是否有脚蹼]
return dataSet, labels
查看结果
data, label = createDataSet()
>>>data [[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
print(calcShannonEnt(data))
>>>0.9709505944546686
# 熵越高,则混合的数据也越多
data[0][2] = "maybe"
print(calcShannonEnt(data))
>>>1.3709505944546687
得到熵之后,我们就可以按照获取最大信息增益的方法划分数据集
划分数据集
分类算法除了需要测量信息熵,还需要划分数据集,度量花费数据集的熵,以便判断当前是否正确地划分了数据集。我们将对每个特征划分数据集的结果计算一次信息熵,然后判断按照哪个特征划分数据集是最好的划分方式。
# 按照给定特征划分数据集
def splitDataSet(dataSet, axis, value):
# (待划分的数据集、划分数据集的特征索引、特征的返回值)
# 该函数是为了将划分的左右提取出来
retDataSet = []
for featVec in dataSet:
# print("1",featVec)
if featVec[axis] == value:
# print("2",featVec[axis])
reducedFeatVec = featVec[:axis]
# print("3",reducedFeatVec)
reducedFeatVec.extend(featVec[axis+1:])
# print("4",reducedFeatVec)
retDataSet.append(reducedFeatVec)
# print("5",retDataSet)
return retDataSet
查看结果
print(splitDataSet(data, 0, 1))
[[1, 'yes'], [1, 'yes'], [0, 'no']]
print(splitDataSet(data,1,1))
[[1, 'yes'], [1, 'yes'], [0, 'no'], [0, 'no']]
'''
在这里 我很疑惑为什么特征返回值都要设置为1呢
在最后我们得出答案 我们将其设置为1的原因是 具体到文字 1代表有脚蹼 或者 不可离开水生活
而我们需要选择一个最优异的特征去划分数据集
举个例子:假如我们选择第一个特征为1(有脚蹼)的这样一条规则去划分
就可以分出有脚蹼和无脚蹼两类大数据 然后我们判断这两类数据中是否可以很好的代表 是不是鱼?
通俗的说就是 由特征1划分出的分类1中的数据
判断是鱼的个数多一点(yes数目多一点)分类2中 判断不是鱼的个数多一点(no数目多一点)
继续看特征2划分的两个子集 还是如上方法 最后将信息增益作对比就可以获得最优划分了
最后结果中我们还会有真实数据的对比 就可以很清楚了
'''
接下来我们将遍历整个数据集,循环计算香农熵和划分数据集,找到最好的特征划分方式。熵计算将会告诉我们如何划分数据集是最好的数据组织方式。
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 计算特征的数目
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的原始香农熵 用于与划分完的数据集的香农熵进行比较
bestInfoGain = 0.0 # 最佳信息增益初始化
bestFeature = -1 # 最佳划分特征初始化 TheBestFeatureToSplit
for i in range(numFeatures): # 遍历所有的特征
featList = [example[i] for example in dataSet] # 使用列表推导式创建列表 用于储存每一个数据的第i个特征
# [ 表达式 for 变量 in 序列或迭代对象 ] 在这里的执行效果就是 每一列的特征都提取出来
# aList = [ x ** 2 for x in range(10) ]
# >>>aList [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
uniqueVals = set(featList) # 特征去重
newEntropy = 0.0 # 划分后信息熵初始化
for value in uniqueVals: # 遍历去重后的特征 分别计算每一个划分后的香农熵
subDataSet = splitDataSet(dataSet, i, value) # 划分
prob = len(subDataSet)/float(len(dataSet)) # 算概率
newEntropy += prob * calcShannonEnt(subDataSet) # 算熵
infoGain = baseEntropy - newEntropy # 计算信息增益
if (infoGain > bestInfoGain): # 比较划分后的数据集的信息增益是否大于0 大于0 证明划分的有效
bestInfoGain = infoGain # 储存最佳信息增益值
bestFeature = i # 储存最佳特征值索引
return bestFeature # 返回最佳特征值索引
结果返回
# print("最好的特征索引:", chooseBestFeatureToSplit(data))
>>> 最好的特征索引:0
>"""
>>>data
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
代码运行结果告诉我们,第0个特征是最好的用于划分数据集的特征。结果是否正确呢?这个结果又有什么实际意义呢?
让我们回头再看一下数据集data中的数据。如果我们按照第一个特征属性划分数据
也就是说第一个特征是1的放在一个组,第一个特征是0的放在另一个组
数据一致性如何?
按照上述的方法划分数据集
第一个特征为1的海洋生物分组将有两个属于鱼类一个属于非鱼类;另一个分组则全部属于非鱼类。
如果按照第二个特征分组,结果又是怎么样呢?
第一个海洋动物分组将有两个属于鱼类,两个属于非鱼类;另一个分组则只有一个非鱼类。
第一个特征代表不可以浮出水面 我们都知道鱼要生活在水里 与有没有脚蹼对比 1特征更为关键
到此时 我们应该对决策树的数据集划分有了进一步的理解
最优特征就是我们的划分条件 根节点数据集 通过 划分条件 划分为两个子节点 是鱼 不是鱼
一层的效果是这样 如果是多层的话 就可以实现对一未知事物的逐步推测了
"""
递归构建决策树
目前我们已经学习了从数据集构造决策树算法所需要的子功能模块,其工作原理如下:得到原始数据集,然后基于最好的属性值划分数据集,由于特征值可能多于两个,因此可能存在大于 两个分支的数据集划分。第一次划分之后,数据将被向下传递到树分支的下一个节点,在这个节点上,我们可以再次划分数据。因此我们可以采用递归的原则处理数据集。
递归结束的条件是:程序遍历完所有划分数据集的属性,或者每个分支下的所有实例都具有 相同的分类。如果所有实例具有相同的分类,则得到一个叶子节点或者终止块。任何到达叶子节点的数据必然属于叶子节点的分类,参见图3-2所示。

第一个结束条件使得算法可以终止,我们甚至可以设置算法可以划分的最大分组数目。如果数据集已经处理了所有属性,但是类标签依然不是唯一的,此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决 定该叶子节点的分类。
"""
函数名称:majorityCnt()
函数说明:统计classList中出现次数最多的元素(类标签)与K-近邻邻近K个元素排序函数功能一致
背景:如果数据集已经处理了所有属性,但是类标签依然不是唯一的
此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决定该叶子节点的分类。
Parameters:
classList:类标签列表
Returns:
sortedClassCount[0][0]:出现次数最多的元素(类标签)
"""
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
创建数的函数代码
"""
函数名称:createTree()
函数说明:
递归构建决策树
对算法步骤和具体递归赋值操作要多注意
parameters:
dataSet:数据集
labels:分类属性标签
returns:
myTres:决策树
"""
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList): # ["yes","yes"]
return classList[0] # 结束划分 如果只有一种分类属性 属性标签重复
if len(dataSet[0]) == 1: # 结束划分 如果没有更多的特征了 都为同一类属性标签了
return majorityCnt(classList) # 计数排序 取最大数特征
bestFeat = chooseBestFeatureToSplit(dataSet) # 获取最优特征索引
bestFeatLabel = labels[bestFeat] # 获取最优特征属性标签
myTree = {bestFeatLabel: {}} # 决策树初始化 嵌套字典
# print("0tree", myTree)
del(labels[bestFeat]) # 删除已经使用的特征标签 这时应只剩下有脚蹼特征了
featValues = [example[bestFeat] for example in dataSet] # 取出数据集所有最优属性值
uniqueVals = set(featValues) # 去重
# print("标签%s,标签值%s" % (bestFeatLabel, uniqueVals))
# 开始构建决策树
for value in uniqueVals:
subLabels = labels[:] # 得到剩下的所有特征标签 作为我们的子节点可用
# print("1tree", myTree)
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
# 对no surfacing特征 值为1时的赋值是最后一次filppers特征全部分类完毕后
# 才将整个filppers的字典值给了关键字1
# abc = {"s":{}}
# abc["s"][0] = "2"
# print(abc) {'s': {0: '2'}}
# print("2tree", myTree)
return myTree
Return
data, label = createDataSet()
mytree = createTree(data, label)
print("mytree:",mytree)
# {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
到这里为止,第一部分的接触就已经算完成了,下一篇我将利用MatPlotLib注解绘制决策树。
总结
决策树由于其容易理解的分类结构,让我产生了很简单的误解,第一次接触,在熵的理解、最佳数据集的划分以及到最后的“递归造树”,单拉出来刚理解,结果混到一起又折腾了我有段时间,当中有很多抽象的数据需要我去一个一个搞清楚,所以我打印了很多,将算法的步骤也理解的差不多了,虽然不是很明确,但是也算努力有所收获,End。