20200510第十一周周结

本周打了两场cf，第一场因为系统原因没有算分，我也该庆幸，毕竟那一场div2我接近半个小时才出A题，确实是十分慢了，C题看了半个多小时也没看懂题意，最终出了两个题。第二场div4七个题才出了三个，我觉得主要原因就是我做题太慢，思路跟不上，也是比较遗憾的。
下面给出部分题的题解
2020.05.06Div2
A. Puzzle Pieces
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a special jigsaw puzzle consisting of n⋅m identical pieces. Every piece has three tabs and one blank, as pictured below.

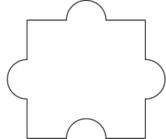
The jigsaw puzzle is considered solved if the following conditions hold:

The pieces are arranged into a grid with n rows and m columns.
For any two pieces that share an edge in the grid, a tab of one piece fits perfectly into a blank of the other piece.
Through rotation and translation of the pieces, determine if it is possible to solve the jigsaw puzzle.

Input
The test consists of multiple test cases. The first line contains a single integer t (1≤t≤1000) — the number of test cases. Next t lines contain descriptions of test cases.

Each test case contains two integers n and m (1≤n,m≤105).

Output
For each test case output a single line containing “YES” if it is possible to solve the jigsaw puzzle, or “NO” otherwise. You can print each letter in any case (upper or lower).

Example
inputCopy
3
1 3
100000 100000
2 2
outputCopy
YES
NO
YES
Note
For the first test case, this is an example solution:

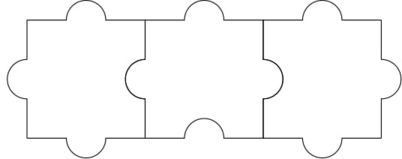
For the second test case, we can show that no solution exists.

For the third test case, this is an example solution:

这个题直接用凹凸部分总数计算即可。每个图形三个凸点，一个凹点，组成后的图形共3* m* n个凸点，外围最多有2*（m+n）个凸点，据此判断能否组成图形即可。

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long t,n,m;
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        if(m*n<=m+n) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

B. Card Constructions
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
A card pyramid of height 1 is constructed by resting two cards against each other. For h>1, a card pyramid of height h is constructed by placing a card pyramid of height h−1 onto a base. A base consists of h pyramids of height 1, and h−1 cards on top. For example, card pyramids of heights 1, 2, and 3 look as follows:

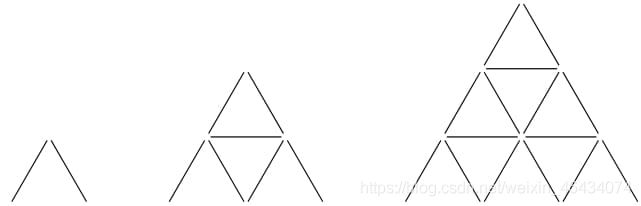
You start with n cards and build the tallest pyramid that you can. If there are some cards remaining, you build the tallest pyramid possible with the remaining cards. You repeat this process until it is impossible to build another pyramid. In the end, how many pyramids will you have constructed?

Input
Each test consists of multiple test cases. The first line contains a single integer t (1≤t≤1000) — the number of test cases. Next t lines contain descriptions of test cases.

Each test case contains a single integer n (1≤n≤109) — the number of cards.

It is guaranteed that the sum of n over all test cases does not exceed 109.

Output
For each test case output a single integer — the number of pyramids you will have constructed in the end.

Example
inputCopy
5
3
14
15
24
1
outputCopy
1
2
1
3
0
Note
In the first test, you construct a pyramid of height 1 with 2 cards. There is 1 card remaining, which is not enough to build a pyramid.

In the second test, you build two pyramids, each of height 2, with no cards remaining.

In the third test, you build one pyramid of height 3, with no cards remaining.

In the fourth test, you build one pyramid of height 3 with 9 cards remaining. Then you build a pyramid of height 2 with 2 cards remaining. Then you build a final pyramid of height 1 with no cards remaining.

In the fifth test, one card is not enough to build any pyramids.
首先用数学方法判断它能组成的最高高度，再用总数减去最高高度所用数量，直到连高度为1的塔都组不成为止，计算即可

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long t,n,m,ans,cnt;
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n;
        cnt=0;
        ans=(sqrt(1+24*n)-1)/6;
        while(ans>=1)
        {
            cnt++;
            n-=(ans+3*ans*ans)/2;
            ans=(sqrt(1+24*n)-1)/6;
        }
        cout<<cnt<<endl;
    }
    return 0;
}

C. Hilbert’s Hotel
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Hilbert’s Hotel is a very unusual hotel since the number of rooms is infinite! In fact, there is exactly one room for every integer, including zero and negative integers. Even stranger, the hotel is currently at full capacity, meaning there is exactly one guest in every room. The hotel’s manager, David Hilbert himself, decides he wants to shuffle the guests around because he thinks this will create a vacancy (a room without a guest).

For any integer k and positive integer n, let kmodn denote the remainder when k is divided by n. More formally, r=kmodn is the smallest non-negative integer such that k−r is divisible by n. It always holds that 0≤kmodn≤n−1. For example, 100mod12=4 and (−1337)mod3=1.

Then the shuffling works as follows. There is an array of n integers a0,a1,…,an−1. Then for each integer k, the guest in room k is moved to room number k+akmodn.

After this shuffling process, determine if there is still exactly one guest assigned to each room. That is, there are no vacancies or rooms with multiple guests.

Input
Each test consists of multiple test cases. The first line contains a single integer t (1≤t≤104) — the number of test cases. Next 2t lines contain descriptions of test cases.

The first line of each test case contains a single integer n (1≤n≤2⋅105) — the length of the array.

The second line of each test case contains n integers a0,a1,…,an−1 (−109≤ai≤109).

It is guaranteed that the sum of n over all test cases does not exceed 2⋅105.

Output
For each test case, output a single line containing “YES” if there is exactly one guest assigned to each room after the shuffling process, or “NO” otherwise. You can print each letter in any case (upper or lower).

Example
inputCopy
6
1
14
2
1 -1
4
5 5 5 1
3
3 2 1
2
0 1
5
-239 -2 -100 -3 -11
outputCopy
YES
YES
YES
NO
NO
YES
Note
In the first test case, every guest is shifted by 14 rooms, so the assignment is still unique.

In the second test case, even guests move to the right by 1 room, and odd guests move to the left by 1 room. We can show that the assignment is still unique.

In the third test case, every fourth guest moves to the right by 1 room, and the other guests move to the right by 5 rooms. We can show that the assignment is still unique.

In the fourth test case, guests 0 and 1 are both assigned to room 3.

In the fifth test case, guests 1 and 2 are both assigned to room 2.
直接看代码就ok

    #include 
    using namespace std;
    #define ll long long int
    #define pb push_back
     
    int main(){
    	ios_base::sync_with_stdio(false);
    	cin.tie(NULL);
    	cout.tie(NULL);
     
    	#ifndef ONLINE_JUDGE
    	freopen("input.txt","r",stdin);
    	freopen("output.txt","w",stdout);
    	#endif

        int t;cin >> t;

        while(t--){
            int n;cin >> n;

            vector<int> a(n,0);
            bool ans=true;
            vector<int> v(n);
            for(int i=0;i<n;i++){
                cin >> v[i];
                v[i]+=i;
                v[i]+=(1e9);
                v[i]%=n;
                a[v[i]]++;
            }
            for(int i=0;i<n;i++){
                if(a[i]==0){cout <<"NO"<<endl;ans=false;break;}
            }
            if(ans)cout <<"YES"<<endl;
        }
    	return 0;
    }

2020.05.09Div4
A. Sum of Round Numbers
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
A positive (strictly greater than zero) integer is called round if it is of the form d00…0. In other words, a positive integer is round if all its digits except the leftmost (most significant) are equal to zero. In particular, all numbers from 1 to 9 (inclusive) are round.

For example, the following numbers are round: 4000, 1, 9, 800, 90. The following numbers are not round: 110, 707, 222, 1001.

You are given a positive integer n (1≤n≤104). Represent the number n as a sum of round numbers using the minimum number of summands (addends). In other words, you need to represent the given number n as a sum of the least number of terms, each of which is a round number.

Input
The first line contains an integer t (1≤t≤104) — the number of test cases in the input. Then t test cases follow.

Each test case is a line containing an integer n (1≤n≤104).

Output
Print t answers to the test cases. Each answer must begin with an integer k — the minimum number of summands. Next, k terms must follow, each of which is a round number, and their sum is n. The terms can be printed in any order. If there are several answers, print any of them.

Example
inputCopy
5
5009
7
9876
10000
10
outputCopy
2
5000 9
1
7
4
800 70 6 9000
1
10000
1
10
这个题本来很简单，把各个位上的数字分开即可，但是我硬是好久才AC，主要是刚开始想的太复杂，判断它是几位数啥的都是没必要的

#include
using namespace std;
int t,n,ans,cnt,a,b,c,d;
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n;
        ans=n;
        cnt=0;
        a=n/1000;
        b=(n-a*1000)/100;
        c=(n-a*1000-100*b)/10;
        d=(n-a*1000-100*b-10*c)%10;
        if(a) cnt++;
        if(b) cnt++;
        if(c) cnt++;
        if(d) cnt++;
        cout<<cnt<<endl;
        if(a)
            cout<<a<<"000 ";
        if(b)
            cout<<b<<"00 ";
        if(c)
            cout<<c<<"0 ";
        if(d)
            cout<<d<<" ";
        cout<<endl;
    }
    return 0;
}

B. Same Parity Summands
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given two positive integers n (1≤n≤109) and k (1≤k≤100). Represent the number n as the sum of k positive integers of the same parity (have the same remainder when divided by 2).

In other words, find a1,a2,…,ak such that all ai>0, n=a1+a2+…+ak and either all ai are even or all ai are odd at the same time.

If such a representation does not exist, then report it.

Input
The first line contains an integer t (1≤t≤1000) — the number of test cases in the input. Next, t test cases are given, one per line.

Each test case is two positive integers n (1≤n≤109) and k (1≤k≤100).

Output
For each test case print:

YES and the required values ai, if the answer exists (if there are several answers, print any of them);
NO if the answer does not exist.
The letters in the words YES and NO can be printed in any case.

Example
inputCopy
8
10 3
100 4
8 7
97 2
8 8
3 10
5 3
1000000000 9
outputCopy
YES
4 2 4
YES
55 5 5 35
NO
NO
YES
1 1 1 1 1 1 1 1
NO
YES
3 1 1
YES
111111110 111111110 111111110 111111110 111111110 111111110 111111110 111111110 111111120

#include
using namespace std;
long long t,n,ans,cnt,k,i,j;
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n>>k;
        ans=n-k+1;
        cnt=n-2*k+2;
        if(ans%2==1&&(ans>0))
        {
            cout<<"YES"<<endl;
            for(i=1;i<=k-1;i++)
                cout<<"1 ";
            cout<<ans<<endl;
        }
        else if(cnt%2==0&&cnt>0)
        {
            cout<<"YES"<<endl;
            for(i=1;i<=k-1;i++)
                cout<<"2 ";
            cout<<cnt<<endl;
        }
        else cout<<"NO"<<endl;
    }
    return 0;
}

C. K-th Not Divisible by n
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given two positive integers n and k. Print the k-th positive integer that is not divisible by n.

For example, if n=3, and k=7, then all numbers that are not divisible by 3 are: 1,2,4,5,7,8,10,11,13…. The 7-th number among them is 10.

Input
The first line contains an integer t (1≤t≤1000) — the number of test cases in the input. Next, t test cases are given, one per line.

Each test case is two positive integers n (2≤n≤109) and k (1≤k≤109).

Output
For each test case print the k-th positive integer that is not divisible by n.

Example
inputCopy
6
3 7
4 12
2 1000000000
7 97
1000000000 1000000000
2 1
outputCopy
10
15
1999999999
113
1000000001
1

#include
using namespace std;
long long t,n,ans,cnt,k,i,j;
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n>>k;
        if(k%(n-1)!=0)
        {
            ans=k/(n-1)+1;///周期
            cnt=(ans-1)*n+1;///周期开始数字
            cnt+=k-(ans-1)*(n-1)-1;
            cout<<cnt<<endl;
        }
        else
        {
            ans=k/(n-1);///周期
            cnt=(ans-1)*n+1;///周期开始数字
            cnt+=k-(ans-1)*(n-1)-1;
            cout<<cnt<<endl;
        }
    }
    return 0;
}

D. Alice, Bob and Candies
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
There are n candies in a row, they are numbered from left to right from 1 to n. The size of the i-th candy is ai.

Alice and Bob play an interesting and tasty game: they eat candy. Alice will eat candy from left to right, and Bob — from right to left. The game ends if all the candies are eaten.

The process consists of moves. During a move, the player eats one or more sweets from her/his side (Alice eats from the left, Bob — from the right).

Alice makes the first move. During the first move, she will eat 1 candy (its size is a1). Then, each successive move the players alternate — that is, Bob makes the second move, then Alice, then again Bob and so on.

On each move, a player counts the total size of candies eaten during the current move. Once this number becomes strictly greater than the total size of candies eaten by the other player on their previous move, the current player stops eating and the move ends. In other words, on a move, a player eats the smallest possible number of candies such that the sum of the sizes of candies eaten on this move is strictly greater than the sum of the sizes of candies that the other player ate on the previous move. If there are not enough candies to make a move this way, then the player eats up all the remaining candies and the game ends.

For example, if n=11 and a=[3,1,4,1,5,9,2,6,5,3,5], then:

move 1: Alice eats one candy of size 3 and the sequence of candies becomes [1,4,1,5,9,2,6,5,3,5].
move 2: Alice ate 3 on the previous move, which means Bob must eat 4 or more. Bob eats one candy of size 5 and the sequence of candies becomes [1,4,1,5,9,2,6,5,3].
move 3: Bob ate 5 on the previous move, which means Alice must eat 6 or more. Alice eats three candies with the total size of 1+4+1=6 and the sequence of candies becomes [5,9,2,6,5,3].
move 4: Alice ate 6 on the previous move, which means Bob must eat 7 or more. Bob eats two candies with the total size of 3+5=8 and the sequence of candies becomes [5,9,2,6].
move 5: Bob ate 8 on the previous move, which means Alice must eat 9 or more. Alice eats two candies with the total size of 5+9=14 and the sequence of candies becomes [2,6].
move 6 (the last): Alice ate 14 on the previous move, which means Bob must eat 15 or more. It is impossible, so Bob eats the two remaining candies and the game ends.
Print the number of moves in the game and two numbers:

a — the total size of all sweets eaten by Alice during the game;
b — the total size of all sweets eaten by Bob during the game.
Input
The first line contains an integer t (1≤t≤5000) — the number of test cases in the input. The following are descriptions of the t test cases.

Each test case consists of two lines. The first line contains an integer n (1≤n≤1000) — the number of candies. The second line contains a sequence of integers a1,a2,…,an (1≤ai≤1000) — the sizes of candies in the order they are arranged from left to right.

It is guaranteed that the sum of the values of n for all sets of input data in a test does not exceed 2⋅105.

Output
For each set of input data print three integers — the number of moves in the game and the required values a and b.

Example
input
7
11
3 1 4 1 5 9 2 6 5 3 5
1
1000
3
1 1 1
13
1 2 3 4 5 6 7 8 9 10 11 12 13
2
2 1
6
1 1 1 1 1 1
7
1 1 1 1 1 1 1
output
6 23 21
1 1000 0
2 1 2
6 45 46
2 2 1
3 4 2
4 4 3

#include 

using namespace std;

int main() {
	int t;
	cin >> t;
	while (t--) {
		int n;
		cin >> n;
		vector<int> a(n);
		for (auto &it : a) cin >> it;
		int l = 0, r = n - 1;
		int suml = 0, sumr = 0;
		int cnt = 0, ansl = 0, ansr = 0;
		while (l <= r) {
			if (cnt % 2 == 0) {
				int nsuml = 0;
				while (l <= r && nsuml <= sumr) {
					nsuml += a[l++];
				}
				ansl += nsuml;
				suml = nsuml;
			} else {
				int nsumr = 0;
				while (l <= r && nsumr <= suml) {
					nsumr += a[r--];
				}
				ansr += nsumr;
				sumr = nsumr;
			}
			++cnt;
		}
		cout << cnt << " " << ansl << " " << ansr << endl;
	}
}