matlab学习(五)数据插值与曲线拟合
一、数据插值
数据插值的计算机制 :
从数学上来说,数据插值是一种函数逼近的方法。
近似函数φ(x) ≈ 未知函数f(x)
在MATLAB中,一维插值函数为interp1(),其调用格式为: Y1=interp1(X,Y,X1,method) 该语句将根据X、Y的值,计算函数在X1处的值。其中,X、Y是两个等长 的已知向量,分别表示采样点和采样值。X1是一个向量或标量,表示要 插值的点。
method参数用于指定插值方法,常用的取值有以下四种:
(1)linear:线性插值,默认方法。将与插值点靠近的两个数据点用直线连 接,然后在直线上选取对应插值点的数据。 (2)nearest:最近点插值。选择最近样本点的值作为插值数据。
(3)pchip:分段3次埃尔米特插值。采用分段三次多项式,除满足插值条 件,还需满足在若干节点处相邻段插值函数的一阶导数相等,使得曲线光 滑的同时,还具有保形性。
(4)spline:3次样条插值。每个分段内构造一个三次多项式,使其插值 函数除满足插值条件外,还要求在各节点处具有连续的一阶和二阶导数。
线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点 n无关。n越大,误差越小。
3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言,3次 埃尔米特插值具有保形性;而3次样条插值要求其二阶导数也连续,所以插 值函数的性态更好。
样例一:零件加工问题,在飞机制造中,机翼的加工是一项关键技术。由于机翼尺寸很大,通常 在图纸中只能标出一些关键点的数据。
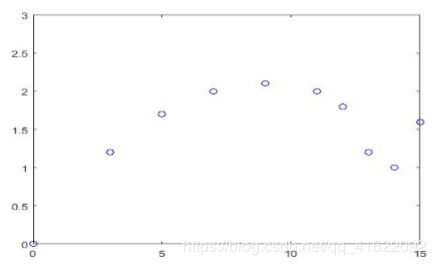
>> x=[0,3,5,7,9,11,12,13,14,15];
>> y=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
>> x1=0:0.1:15;
>> y1=interp1(x,y,x1,'spline');
>> plot(x1,y1)

MATLAB中的二维插值函数为interp2(),其调用格式为: Z1=interp2(X,Y,Z,X1,Y1,method) 其中,X、Y是两个向量,表示两个参数的采样点,Z是采样 点对应的函数值。X1、Y1是两个标量或向量,表示要插值 的点。
样例二:粮储仓的通风控制问题
在某粮情自动测控系统中,根据粮温、粮湿计算平衡点湿度,与大气湿 度进行比较,再根据通风模拟情况决定是否自动进行通风。已测得平衡 点湿度与粮温、粮湿关系的部分数据如下表,请推算相应范围内温度每 变化1度、湿度每变化1个点的平衡点湿度。
>> x=20:10:90;
>> y=(0:5:20)';
>> z=[8.9,10.32,11.3,12.5,13.9,15.3,17.8,21.3; 8.7,10.8,11,12.1,13.2,14.8,16.55,20.8; 8.3,9.65,10.88,12,13.2,14.6,16.4,20.5; 8.1,9.4,10.7,11.9,13.1,14.5,16.2,20.3; 8.1,9.2,10.8,12,13.2,14.8,16.9,20.9];
>> xi=20:90;
>> yi=(0:20)';
>> zi=interp2(x,y,z,xi,yi,'spline');
>> surf(xi,yi,zi)
subplot(2,2,1)
x=0:200:1800;
y=x';
z=[2000,2000,2001,1992,1954,1938,1972,1995,1999,1999; 2000,2002,2006,1908,1533,1381,1728, 1959,1998,2000; 2000,2005,2043,1921,977,897,1310,1930,2003,2000; 1997,1978,2009,2463,2374,1445,1931,2209,2050,2003; 1992,1892,1566,1971,2768,2111,2653,2610,2121,2007; 1991,1875,1511,1556,2221,1986,2660,2601,2119,2007; 1996,1950,1797,2057,2849,2798,2608,2303,2052,2003; 1999,1999,2079,2685,3390,3384,2781,2165,2016,2000; 2000,2002,2043,2271,2668,2668,2277,2049,2003,2000; 2000,2000,2004,2027,2067,2067,2027,2004,2000,2000];
surf(x,y,z);
subplot(2,2,2)
x1=0:100:1800;
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
surf(x1,y1,z1);
subplot(2,2,3)
x2=0:50:1800;
y2=x2';
z2=interp2(x1,y1,z1,x2,y2,'spline');
surf(x2,y2,z2);
subplot(2,2,4)
contour(x2,y2,z2,12)
二、曲线拟合
与数据插值类似,曲线拟合也是一种函数逼近的方法。
构造函数g(x)去逼近未知函数f(x),使得误差 δi= g(xi)-f(xi)(i=1,2,3,…,n) 在某种意义下达到最小。
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误 差的平方和来寻找数据的最佳函数匹配。
MATLAB中的多项式拟合函数为polyfit(),其功能为求得最小二乘拟合多项式系 数,其调用格式为:
(1)P=polyfit(X,Y,m) (2)[P,S]=polyfit(X,Y,m) (3)[P,S,mu]=polyfit(X,Y,m):根据样本数据X和Y,产生一个m次多项式P及 其在采样点误差数据S,mu是一个二元向量,mu(1)是mean(X),而mu(2)是 std(X)。
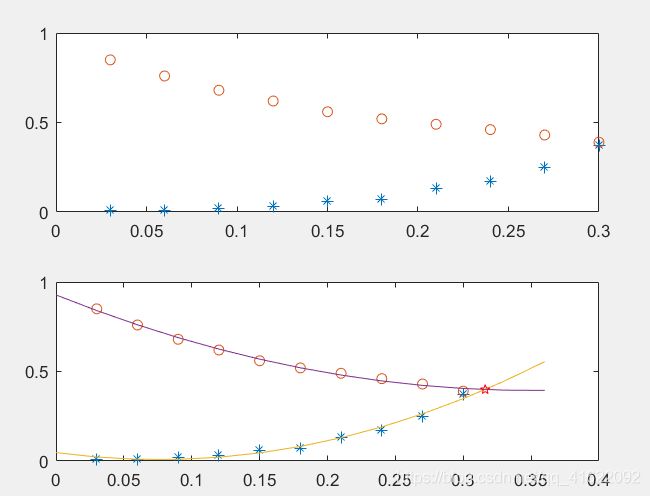
样例四:算法的参数优化问题
在群体智能优化算法的设计中,搜索行为具有一定的随机性,以免于陷入局部最优。 但是,随机性参数的设置却是一个普遍性的难题。如果随机性过高,算法的多样性增 加,但是难以收敛;若随机性太低,算法收敛速度快,但多样性降低,极有可能陷入 局部最优。已知某算法随机性参数与多样性、收敛性的关系分别如表1和表2所示,其 中收敛性与多样性数据都已经转换为与算法性能相关的统一度量。现在算法的设计者 既不愿意降低收敛性,又不愿意牺牲多样性,想要在两者之间取得一个平衡点。请问 怎么确定随机性参数?
subplot(2,1,1)
x=0.03:0.03:0.3;
y1=[0.01,0.01,0.02,0.03,0.06,0.07,0.13,0.17,0.25,0.37];
y2=[0.85,0.76,0.68,0.62,0.56,0.52,0.49,0.46,0.43,0.39];
plot(x,y1,'*',x,y2,'o');
subplot(2,1,2)
p1=polyfit(x,y1,2);
p2=polyfit(x,y2,2);
p=p1-p2;
xi=roots(p);
xj=0:0.03:0.36;
yj1=polyval(p1,xj);
yj2=polyval(p2,xj);
yi=polyval(p1,xi(2))
plot(x,y1,'*',x,y2,'o',xj,yj1,xj,yj2,xi(2),yi,'rp');
三、数据插值与曲线拟合的比较
相同点: 都属于函数逼近方法
都能进行数据估算
不同点: 实现方法不同
结果形式不同
侧重点不同
应用场合不同

