Codeforces Global Round 8abcd简单题解

A. C+=

B. Codeforces Subsequences

C. Even Picture

D. AND, OR and square sum

A. C+=

题意：
给你t组测试用例，每组测试用例三个正整数a,b,n;
每次操作能使a+=b或b+=a；
问最少几次操作使得a或b严格大于n；
$$数据范围：a,b,n(1\le a,b\le n\le 10^9)$$
我的理解：
贪心每次操作，让min(a,b)+=max(a,b);
代码：

#include 
#define ll long long
#define ld long double
using namespace std;

ll t,a,b,c;
void run(){
    cin>>a>>b>>c;
    k=0;
    if(a>b)swap(a,b);
    while(a<=c||b<=c){
        if(k&1)b+=a;
        else a+=b;
        k++;
    }
    cout<<k-1<<'\n';
}
int main(){
#ifdef haosao
freopen("main.h", "r", stdin);
#endif
    std::ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
        run();
}

B. Codeforces Subsequences

题意：
给你一个正整数k；
求最短的字符串包含至少k个"codeforces"个子序列；
$$数据范围：k(1\le k\le 10^{16})$$
我的理解：
总所周知：
“ccodeforces"包含两个"codeforces”；
“ccoodeforces"包含四个"codeforces”；
“ccooddeforces"包含八个"codeforces”；
代码：

#include 
#define ll long long
#define ld long double
using namespace std;

ll k,num[11];
void run(){
    cin>>k;
    string s="#codeforces";
    ll n=1;
    for(int i=1;i<=10;i++)num[i]=1;
    while(n<k){
        for(int i=1;i<=10&&n<k;i++){
            n/=num[i];
            num[i]++;
            n *= num[i];
        }
    }
    for(int i=1;i<=10;i++){
        while(num[i]--)cout<<s[i];
    }
}
int main(){
#ifdef haosao
freopen("main.h", "r", stdin);
#endif
    std::ios::sync_with_stdio(false);
    run();
}

C. Even Picture

题意：
在一个无限大的网格中；
给你一个正整数n；
画出一个灰色联通区域，使得
1.每个灰色格子有偶数个灰色格子与之相邻(0,2,4);
2.恰好有n个灰色格子有4个与之相邻的灰色格子(就是g[x,y],g[x+1,y],g[x,y+1],g[x-1,y],g[x,y-1],都是灰色使有n个这样的g[x,y],并满足条件1)；
$$数据范围：n(1\le k\le 500)$$
输出k(灰色格子的数量)
k行，每行一个灰色格子的坐标
我的理解：
手玩，显然：
当n=1时：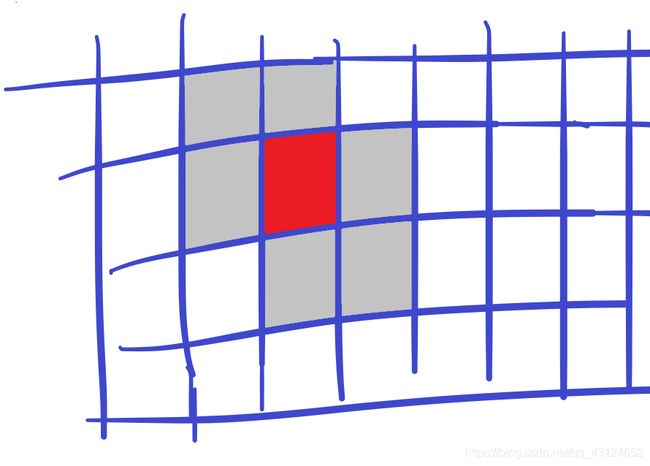
当n=3:

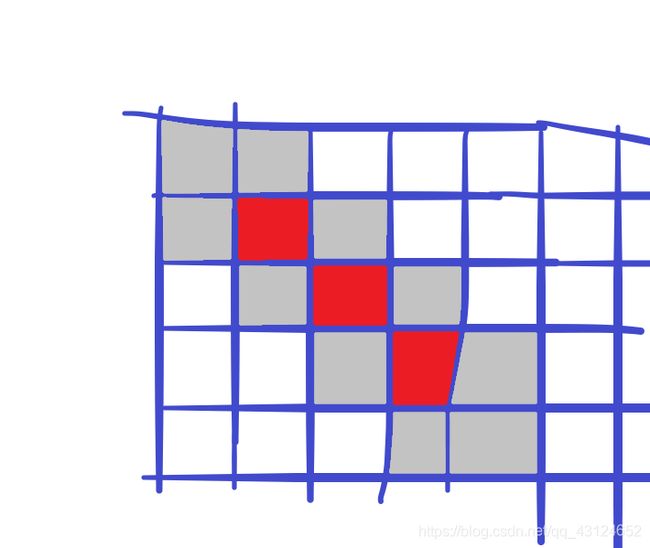
代码：

#include 
#define ll long long
#define ld long double
using namespace std;
ll n;
void run(){
    cin>>n;//500;
    cout<<(n)*3+4<<'\n';
    cout<<"0 0\n0 1\n";
    int l=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<3;j++){
            cout<<i<<" "<<l+j<<'\n';
        }
        l++;
    }
    cout<<n+1<<" "<<l<<'\n'<<n+1<<" "<<l+1<<'\n';
}
int main(){
#ifdef haosao
    freopen("main.h", "r", stdin);
#endif
    std::ios::sync_with_stdio(false);
    run();
}

D. AND, OR and square sum

题意：
给你一个长度为n的数组a，你可以执行任意次以下操作：
选择1<=i,j<=n
令：x=a[i],y=a[j]
a[i]=x&y;a[j]=x|y;
$$求(MAX)sum={\Sigma }_{i=1}^{n}a[i{]}^2$$数据范围：$$n(1\le n\le 2\cdot 10^5)$$$$a1,\dots ,an(0\le ai<2^{20})$$
我的理解：
&和|操作一起，就是一个swap操作，使a[i]和a[j]在二进制下交换所在位
所以数组a中的1总量不变
那么我们就可以贪心使大数尽量的多
代码：

#include 
#define ll long long
#define ld long double
using namespace std;
 
ll n,a[22],b;
void run(){
    cin >> n;
    for(int i=0; i<n; i++){
        cin>>b;
        for(int j=20;j>=0;j--){
            if((1<<j)<=b){
                b-=(1<<j);
                a[j]++;
            }
        }
    }
    ll ans=0;
    for(int i=0; i<n; i++){
        ll tmp=0;
        for(int j=0;j<=20;j++){
            if(a[j]){
                a[j]--;
                tmp+=(1<<j);
            }
        }
        ans+=tmp*tmp;
    }
    cout<<ans<<'\n';
}
int main(){
#ifdef haosao
    freopen("main.h", "r", stdin);
#endif
    std::ios::sync_with_stdio(false);
    run();
}

未完待续~！@#￥%……