546. Remove Boxes 移除盒子

给出一些不同颜色的盒子，盒子的颜色由数字表示，即不同的数字表示不同的颜色。
你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 k*k 个积分。
当你将所有盒子都去掉之后，求你能获得的最大积分和。

示例：

输入：boxes = [1,3,2,2,2,3,4,3,1]
输出：23
解释：
[1, 3, 2, 2, 2, 3, 4, 3, 1] 
----> [1, 3, 3, 4, 3, 1] (3*3=9 分) 
----> [1, 3, 3, 3, 1] (1*1=1 分) 
----> [1, 1] (3*3=9 分) 
----> [] (2*2=4 分)

提示：

• 1 <= boxes.length <= 100
• 1 <= boxes[i] <= 100

动态规划

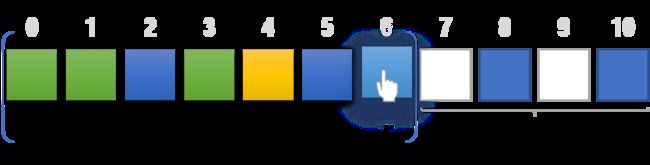
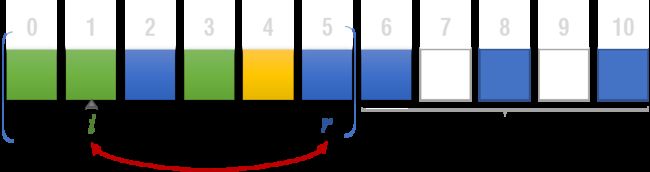
首先，假设我们拿到的 boxes 长这样：

假设我们经过一系列操作后消掉了其中一些盒子：

对于这样一个子序列，我们就可以记录到dp数组里。我们可以操作的范围是l到r的子序列。由于我们对每个子序列默认都是点击boxes[r]来消除，因此要知道r的后面还连着几个与boxes[r]相同颜色的盒子，记为k。如下图，l = 0, r = 6, k = 2， 将其能获得的最高得分记在dp[0][6][2]。

现在我们调用 calculatePoints(i, r, k) 来计算它的最高得分 dp[i][r][k]。

calculatePoints(i, r, k)

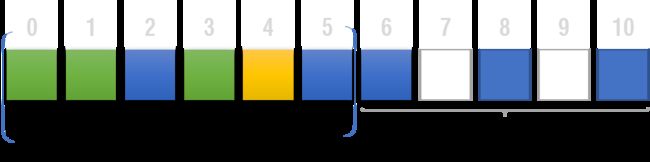
在我们这个子序列中，dp[0][6][2] 与 dp[0][5][3] 实际上是等价的。我们将r向左一直移动到不能再移动为止。

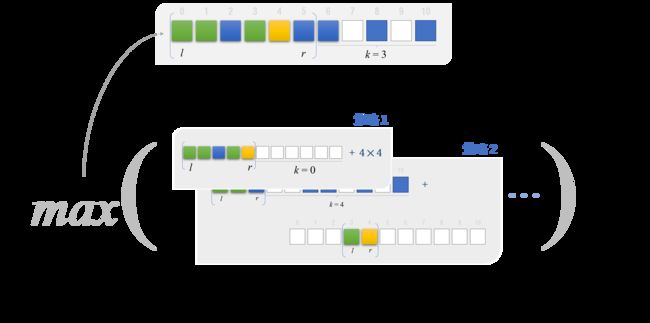
接着，我们计算出不同策略的得分，取最高分。

策略 1

我们可以直接点boxes[r]，把最后4个盒子一次性消除，获得16分！

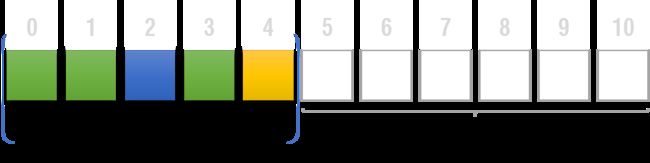
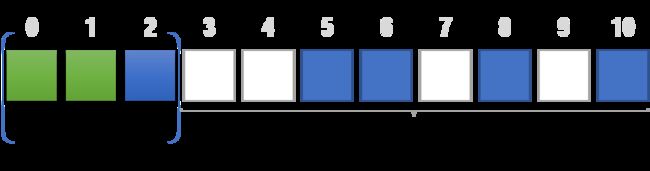
剩下的盒子成为这样一个子序列 dp[0][4][0]：

策略1得分：4*4 + dp[0][4][0]

策略 2

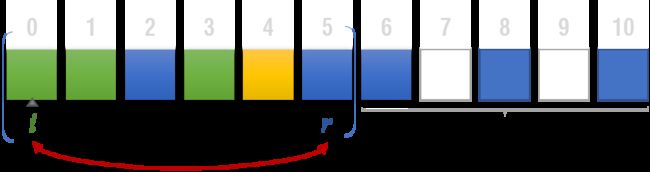
我们还可以把夹在中间的杂鱼盒子都消掉，让后面连起来的盒子数更多：

为了找到可以跟 boxes[r] 连起来的盒子，令 i = l：

i++

直到 boxes[i] == boxes[r]，就说明我们搜索到了

在这个例子中，消掉杂鱼盒子能获得的分数是 dp[3][4][0]。

剩下的盒子的得分是 dp[0][2][4] 。

综上，策略2得分：dp[0][2][4] + dp[3][4][0]

总结

为了取得一个子序列的最高得分，我们分不同策略，每种策略的得分可以看作是1~2个子子序列的最高分之和。

Code

	def removeBoxes(self, boxes: List[int]) -> int:
		def dp(l, r, n):
			nonlocal memo, boxes
			if memo.get((l, r, n)):
				return memo[(l, r, n)]

			if l == r - 1:
				return (n + 1) * (n + 1)

			if boxes[l] == boxes[l + 1]:
				return dp(l + 1, r, n + 1)

			res = (n + 1) * (n + 1) + dp(l + 1, r, 0)
			for l2 in range(l + 2, r):
				if boxes[l2] == boxes[l]:
					res = max(res, dp(l + 1, l2, 0) + dp(l2, r, n + 1))
			memo[(l, r, n)] = res
			return res

		memo = {}
		return dp(0, len(boxes), 0)

复杂度分析

• 时间复杂度：O(n4)O(n^4)O(n4)。最坏情况下每个 $f(l,r,k)$ 被计算一次，每次状态转移需要 $O(n)$ 的时间复杂度。
• 空间复杂度：O(n3)O(n^3)O(n3)。$\mathrm{d}\mathrm{p}$ 数组的空间代价是 O(n3)O(n^3)O(n3)，递归使用栈空间的代价为 $O(n)$。