因为是新生选拔赛所以题目总体不难,但是不乏坑题(数学题和物理题)
题目都是中文题,只要题目没有歧义我基本只会讲解法。
A PUBG
bfs,设一个数组vis[i][j]表示从起点到(i,j)的最小数值,然后bfs就行了。
#include
#include
#include
#include
#include
B precise math function
需要精度高的pi,读者可以直接复制高高精度的pi,或者用acos(-1)表示(笔者推荐后者)
因为要由变量确定精度,所以用c++的iomanip头文件中的输出修正
#include
#include
#include
#include
#include
C 颜料的混合
这里的颜料混合和盐水稀释是一个道理的,所以除了要考虑浓度之外还要注意混合是体积也会有影响。
根据盐水稀释,如果把浓度和体积设为横坐标和纵坐标,两倍盐水能稀释的范围在两点连线上的点。
以此类推,三个点的话能稀释的范围就是在三角形内。
问题转换为点是否在三角形内。
读者可以直接用几何模板,这里笔者提供一种三角形的思路。
如果点在三角形内,那么点把三角形分割成三个三角形,这三个三角形的面积和和原来的一定相等。
#include
#include
#include
#include
#include
D 打篮球
直接模拟就行了
#include
#include
#include
#include
#include
E 233
大数乘法随便来
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
t=int(input())
for x in range(t):
a,b=input().split( )
a=int(a)
b=int(b)
a=a*b
print(a)
F 扫雷
因为如果没有扫到雷要求输出矩阵,所以要设一个数组保留最后答案。
扫到的点分三种
1:扫到雷,直接返回失败。
2:扫到数字,把这个数字赋值给答案数组。
3:扫到.,把剩余的八联通块进行bfs。
#include
#include
#include
#include
#include
G 火车上的2连座
签到题
#include
#include
#include
#include
#include
H 程序员的好印象
实际为一个非严格递增的lis
#include
#include
#include
#include
#include
I 郊游
数学题。非常要命
首先要说一些题目问题。
车和人是同时从起点出发的。题目要求输出的是最短时间,也就是最优解。车是可以随时放人下车和掉头的。
那么先说结论,为了让车被使用的效率最高,除了最后一批人是坐车直接到目的地之外。
每一批人都是 走路一段-》上车-》车走一段-》下车走-》终点的流程。并且人都是同时到达的(包括最后一批坐车的)
车就是在不断来回接人。
之所以不直接载到终点是为了尽量多用车代步使用时减少。
那么问题来了车在哪里放人下车最优。
首先先说几个结论,1:每一批人走的距离是一样的。2:车载每一批人行驶的距离也是一样的(理由是因为要同时到达)
设一共有p批人
对于第一批人,起点为0的位置,如果他们是在x位置下车的,那么车回头和向前走的人相遇地点在2*v1*x/(v1+v2) (这里读者自己证明),设其为y。
对于第二批人起点在y,根据上面的公式可知车会在2*y的位置和向前走的人相遇。
......
第p批的时候起点在(p-1)*y,因为他们是直接坐车到终点的,坐车距离是x
那么有关系式 L-(p-1)*y=x
化简得x=l*(v1 + v2) / (2.0*v1*(p - 1) + v1 + v2)
结果就为x/v2+(l-x)/v1
(数学题惹不起)
#include
#include
#include
#include
#include
J 过河
物理题。
首先要确定一点的是题目要求的是船头一直指向正对岸,这是船是走曲线的。
建立坐标系,设船到起点的坐标为r,水平位移为x
那么有
对两者求积分可得
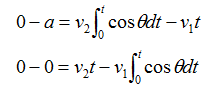
解得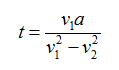
然后因为这是一道原题,读者觉得不清楚可以百度。
题号hdu 5761
#include
#include
#include
#include
#include