算法导论学习笔记01——算法时间复杂度
本篇文章分四部分内容。第1部分简单的给出时间复杂度定义；第2第3部分介绍了插入排序和并归排序的实现，以及这两种算法时间复杂度的计算；第4部分贴出C语言源码，并提供了一种对排序算法正确性测试的方法。
目录
1、时间复杂度定义
2、插入排序及其时间复杂度
2.1 算法实现
2.2 时间复杂度
3、并归排序及其时间复杂度
3.1 算法实现
3.2 时间复杂度
4、代码与测试
4.1 测试代码
4.2 插入排序
4.3 并归排序
1、时间复杂度定义
定义：对于函数 
存在函数 
和常数 
，当 
时，满足不等式：
，则称 是 的一个渐进紧确界。记做：
或 
。
当只有一个边界时，就是渐进上界或渐进下届：
对于函数 存在函数 和常数 
，当 时，满足不等式：
，则称 是 的一个渐进上界。记做：
。
对于函数 存在函数 和常数 ，当 时，满足不等式：
，则称 是 的一个渐进下界。记做：
。
当边界只能大于（小于）而不能等于时，认为边界是渐进的但不是紧确的：
对于函数 存在函数 和常数 ，当 时，满足不等式：
，则称 是 的一个渐进非紧确上界。记做：
。
对于函数 存在函数 和常数 ，当 时，满足不等式：
，则称 是 的一个渐进非紧确下界。记做：
。
我们常说的时间复杂度就是渐进上界。
2、插入排序及其时间复杂度
2.1 算法实现
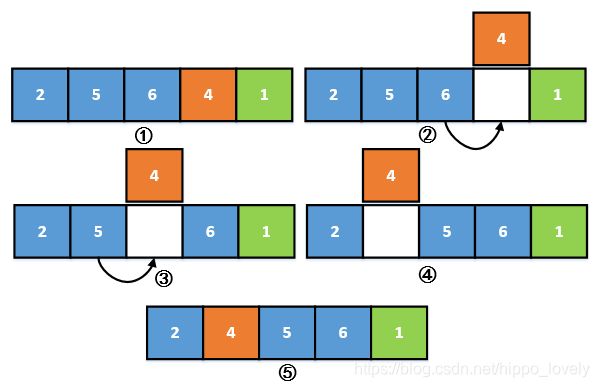
插入排序将n个数字分成2部分，左边（蓝色）的是有序序列，右边（橘色和绿色）的是未排序序列，每次选择未排序序列的第一个数（橘色）将其插入到有序序列中。
下面一组图展示了将一个未排序数插入到已排序序列的过程：
② 将橘色的待排序数取出，在原有位置留下一个空位
③ - ④ 将橘色待排序数从后向前与有序序列进行比较，如果待排序数小，则将与之比较的有序数向后移动到空位中
⑤ 当待排序数在有序序列中找到第一个比它小的数时，停止比较，将待排序数插入到空位中
伪代码如下：
数组的第一个元素为A[0]，开始时认为A[0]是第一个有序序列，从A[1]开始到A[length-1]将每一个未排序数插入到有序序列中。
INSERTION-SORT(A)
for j = 1 to A.length - 1
key = A[j]
i = j - 1
while i >= 0 and A[i] > key
A[i + 1] = A[i]
i = i - 1
A[i + 1] = key2.2 时间复杂度
给伪代码中每一行都可以在一个常数的指令周期中完成，令每一行的代码是
~
。假设代码运行在最坏的情况下，即序列时逆序的，那么：在2行的for循环下，每次循环中5-7行会执行 j 次或 j-1 次，用
表示每个 for 循环时5-7行需要执行的次数，循环从j=1到j=n-1因此5-7行总执行次数为
。因此各行执行次数如下：
得到程序耗时：
故可以得到最坏情况下的运行时间， 即渐进上届
3、并归排序及其时间复杂度
3.1 算法实现
并归排序是分治思想的一种应用，即将一个问题分解成若干个子问题，解决较容易的子问题后，在将子问题的结果合并成原问题的结果。并归排序可以分成以下3步：
① 分解：将需要排序的n个数分解成2个子序列，每个序列有n/2个数
② 解决：使用并归排序递归的排序两个子序列
③ 合并：合并排序后的两个子序列
伪代码如下：
MERGE-SORT(A, p, r)
if p < r
q = (p + r)/2
MERGE-SORT(A, p, q)
MERGE-SORT(A, q + 1, r)
MERGE(A, p, q, r)当 p >= r 的时候递归结束。MERGE函数将长度为 q - r + 1 和 r - q 的两个有序子序列合并成一个有序序列，放在 A[p, r] 中，其实现如下：
MERGE(A, p, q, r)
n1 = q - p + 1
n2 = r - q
let L[0, 1, 2, ... n1] and R[0, 1, 2, ... n2]
for i = 0 to n1 - 1
L[i] = A[p + i]
for i = 0 to n2 - 1
R[i] = A[q + i + 1]
L[n1] = MAX
R[n2] = MAX
i = 0
j = 0
for k = p to r
if L[i] <= R[j]
A[k] = L[i]
i = i + 1
else
A[k] = R[j]
j = j + 1将两个有序序列合成时，每次比较只需要将两个子序列剩余数字的第一个进行比较，选出较小的一个即可。同时在做MERGE时使用了“哨兵”的方法，来使代码更紧凑。
“哨兵”是一个无限大的数，在序列A和子序列B的尾部都增加这样一个“哨兵”。这样在12~18行的循环中，如果序列A已经弹出所有数字，当前只剩“哨兵”。那么在接下来的比较中因为“哨兵”将大于B中剩余的数字，使用这种方法隐式的表明一个序列以到达尾部。
3.2 时间复杂度
我们先来计算MERGE过程的时间复杂度，令MERGE函数需要合并的序列长度为n = r - p + 1：
2 ~ 4 行与 9 ~ 12行都会占用常数的计算时间，总时间为
5 ~ 8 行的两个for循环：循环的次数分别为 p - q + 1 和 r - q，共n次，总时间
13 ~ 19 行for循环：循环次数为r - q + 1 即n次，总时间为
因此得到MERGE过程对n个数进行合并时，时间复杂度为
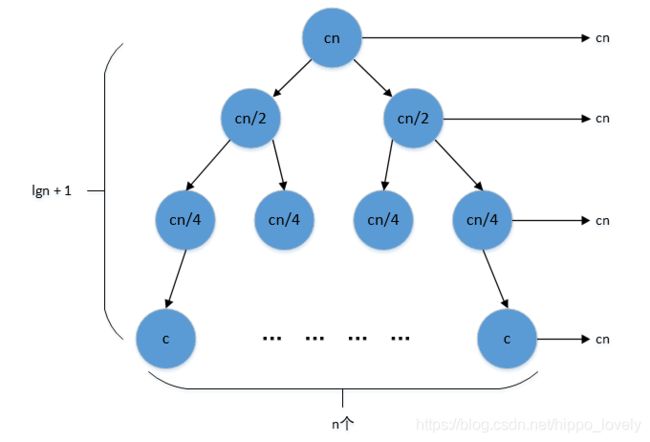
下面来看MERGE-SORT过程的时间复杂度：当n = 1时，只需要进行一次比较即可，令时间为常数c。当n不为1时，递归过程将T(n)转化成了2个T(n/2)任务，以及一个MERGE(n)过程，后者拥有线性的时间复杂度，则递归式可以写成：
递归过程所用时间树如下图所示：
可以看出分治排序的总代价为：
(其中
表示
。因此得到分治排序的时间复杂度为
(注：在计算时间复杂度时，为了方便分析假设lgn是整数，当lgn不是整数时，递归过程时间树每层消耗时间将
，所以
是分治排序的渐进(紧确)上界，当lgn为整数时达到紧确。
4、代码与测试
4.1 测试代码
测试代码包括2部分，第一部分是C代码中的main函数，功能是读取输入参数，生成需要排序的数组arr和数组长度n。然后调用对应的排序算法将数据排序，最后将数组输出。
#include
#include
extern int merge_sort(int A[], int p, int r);
int get_number(int num, int **arr, char *argv[])
{
int i;
*arr = (int *)malloc(sizeof(int) * num);
if (NULL == *arr) {
printf("Error: malloc failed\n");
return -1;
}
for (i = 0; i < num; i ++) {
(*arr)[i] = atoi(argv[i + 1]);
}
return 0;
}
int print_number(int num, int arr[])
{
int i;
for (i = 0; i < num; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
int main(int argc, char *argv[])
{
int num, *arr;
num = argc - 1;
if (get_number(num, &arr, argv)) {
return -1;
}
if (sort(num, arr)) {
return -1;
}
print_number(num, arr);
free(arr);
return 0;
}
第二部分使用python脚本，生成一个小于10000的整数n，然后生成n个随机整数，作为“输入”，调用python的sort函数对“输入”进行排序，作为“答案”。将排序程序的“结果”比照“答案”进行检查，python代码如下：
import os
import random
def do_test(func_str, arg, res):
cmd = func_str + " " + arg
ret = os.popen(cmd).read().strip()
if res != ret:
print "Error case\n" + "case: " + arg + "\nres: " + ret
return -1
return 0
MAX = 2147483647
MIN = -2147483648
TIMES = 10000
MAX_NUMBER = 10000
if __name__ == '__main__':
func = "./sort"
for i in range(TIMES):
number_len = random.randint(1, MAX_NUMBER)
number = [random.randint(MIN, MAX) for i in range(number_len)]
number_s = sorted(number)
arg = ' '.join(str(n) for n in number)
res = ' '.join(str(n) for n in number_s)
ret = do_test(func, arg, res)
if ret == -1:
break
4.2 插入排序
/*
INSERTION-SORT(A)
for j = 1 to A.length - 1
key = A[j]
//INSERT a[j] into the sorted swquence A[1 ... j - 1]
i = j - 1
while i >= 0 and A[i] > key
A[i + 1] = A[i]
i = i - 1
A[i + 1] = key
*/
void insert_sort(int n, int A[])
{
int i, j, key;
for (j = 1; j < n; j++) {
key = A[j];
i = j - 1;
while (i >= 0 && A[i] > key) {
A[i + 1] = A[i];
i--;
}
A[i + 1] = key;
}
return;
}
int sort(int n, int arr[])
{
insert_sort(n, arr);
return 0;
}4.3 并归排序
#include
#include
/*
MERGE(A, p, q, r)
n1 = q - p + 1
n2 = r - q
let L[0, 1, 2, ... n1] and R[0, 1, 2, ... n2]
for i = 0 to n1 - 1
L[i] = A[p + i]
for i = 0 to n2 - 1
R[i] = A[q + i + 1]
L[n1] = MAX
R[n2] = MAX
i = 0
j = 0
for k = p to r
if L[i] <= R[j]
A[k] = L[i]
i = i + 1
else
A[k] = R[j]
j = j + 1
*/
#define BIG ((1 << (sizeof(int) * 8 - 1)) - 1)
int merge(int A[], int p, int q, int r)
{
int n1 = q - p + 1;
int n2 = r - q;
int *L = (int *)malloc(sizeof(int) * (n1 + 1));
if (L == NULL) {
printf("err malloc\n");
return -1;
}
int *R = (int *)malloc(sizeof(int) * (n2 + 1));
if (R == NULL) {
printf("err malloc\n");
free(L);
return -1;
}
int i, j, k;
for (i = 0; i < n1; i++) {
L[i] = A[p + i];
}
for (i = 0; i < n2; i++) {
R[i] = A[q + i + 1];
}
L[n1] = BIG;
R[n2] = BIG;
i = 0;
j = 0;
for (k = p; k <= r; k++) {
if (L[i] <= R[j]) {
A[k] = L[i];
i++;
} else {
A[k] = R[j];
j++;
}
}
free(R);
free(L);
return 0;
}
/*
MERGE-SORT(A, p, r)
if p < r
q = (p + r)/2
MERGE-SORT(A, p, q)
MERGE-SORT(A, q + 1, r)
MERGE(A, p, q, r)
*/
int merge_sort(int A[], int p, int r)
{
if (p < r) {
int q = (p + r) / 2;
merge_sort(A, p, q);
merge_sort(A, q + 1, r);
return merge(A, p, q, r);
}
return 0;
}
int sort(int n, int arr[])
{
return merge_sort(arr, 0, n - 1);
}