深度学习-梯度下降

参考：
https://yjango.gitbooks.io/superorganism/content/ti_du_xia_jiang_xun_lian_fa.html

https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650720663&idx=3&sn=d9f671f77be23a148d1830448154a545&chksm=871b0de9b06c84ffaf260b9ba2a010108cca62d5ce3dcbd8c98c72c9f786f9cd460b27b496ca&scene=0#rd

http://www.jianshu.com/p/695ccab8198e

http://www.cnblogs.com/pinard/p/5970503.html

http://www.cnblogs.com/ooon/p/4947688.html

梯度下降训练法

如何训练：

既然我们希望网络的输出尽可能的接近真正想要预测的值。那么就可以通过比较当前网络的预测值和我们真正想要的目标值，再根据两者的差异情况来更新每一层的权重矩阵（比如，如果网络的预测值高了，就调整权重让它预测低一些。不断调整，直到能够预测出目标值）。
因此就需要先定义“如何比较预测值和目标值的差异”，这便是损失函数或目标函数（loss function or objective function），用于衡量预测值和目标值的差异的方程。loss function的输出值（loss）越高表示差异性越大。那神经网络的训练就变成了尽可能的缩小loss的过程。
所用的方法是梯度下降（Gradient descent）：通过使loss值向当前点对应梯度的反方向不断移动，来降低loss。一次移动多少是由学习速率（learning rate）来控制的。
梯度下降的问题：

然而使用梯度下降训练神经网络拥有两个主要难题。
1、局部极小值(或鞍点)

梯度下降寻找的是loss function的局部极小值，而我们想要全局最小值。如下图所示，我们希望loss值可以降低到右侧深蓝色的最低点，但loss在下降过程中有可能“卡”在左侧的局部极小值中。也有最新研究表明在高维空间下局部极小值通常很接近全局最小值，训练网络时真正与之“斗争”的是鞍点。但不管是什么，其难处就是loss“卡”在了某个位置后难以下降。唯一的区别是：陷入局部极小值就难以出来，陷入鞍点最终会逃脱但是耗时。

试图解决“卡在局部极小值”问题的方法分两大类：
调节步伐：调节学习速率，使每一次的更新“步伐”不同。常用方法有：
随机梯度下降（Stochastic Gradient Descent (SGD)：每次只更新一个样本所计算的梯度
小批量梯度下降（Mini-batch gradient descent）：每次更新若干样本所计算的梯度的平均值
动量（Momentum）：不仅仅考虑当前样本所计算的梯度；Nesterov动量（Nesterov Momentum）：Momentum的改进
Adagrad、RMSProp、Adadelta、Adam：这些方法都是训练过程中依照规则降低学习速率，部分也综合动量
优化起点：合理初始化权重（weights initialization）、预训练网络（pre-train），使网络获得一个较好的“起始点”，如最右侧的起始点就比最左侧的起始点要好。常用方法有：高斯分布初始权重（Gaussian distribution）、均匀分布初始权重（Uniform distribution）、Glorot 初始权重、He初始权、稀疏矩阵初始权重（sparse matrix）
2、梯度的计算

机器学习所处理的数据都是高维数据，该如何快速计算梯度、而不是以年来计算。 其次如何更新隐藏层的权重？ 解决方法是：计算图：反向传播算法 这里的解释留给非常棒的Computational Graphs: Backpropagation+

需要知道的是，反向传播算法是求梯度的一种方法。如同快速傅里叶变换（FFT）的贡献。 而计算图的概念又使梯度的计算更加合理方便。
基本流程图

下面就简单浏览一下训练和识别过程，并描述各个部分的作用。

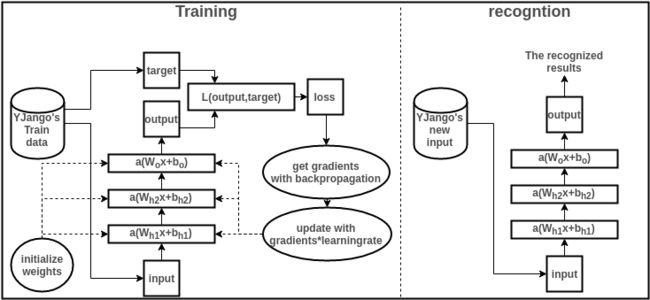
收集训练集（train data）：也就是同时有input以及对应label的数据。每个数据叫做训练样本（sample）。label也叫target，也是机器学习中最贵的部分。上图表示的是我的数据库。假设input的维度是39，label的维度是48。
设计网络结构（architecture）：确定层数、每一隐藏层的节点数和激活函数，以及输出层的激活函数和损失函数。上图用的是两层隐藏层（最后一层是输出层）。隐藏层所用激活函数a( )是ReLu，输出层的激活函数是线性linear（也可看成是没有激活函数）。隐藏层都是1000节点。损失函数L( )是用于比较距离MSE：mean((output - target)^2)。MSE越小表示预测效果越好。训练过程就是不断减小MSE的过程。到此所有数据的维度都已确定：

……..