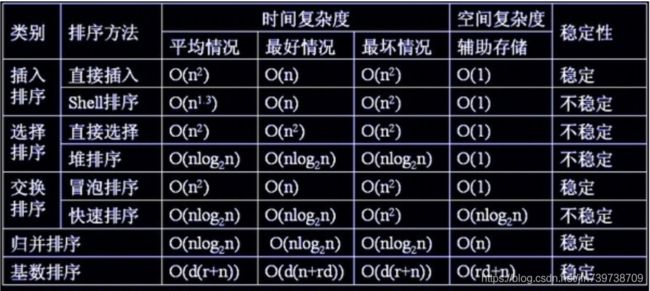
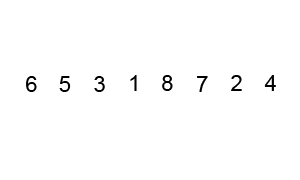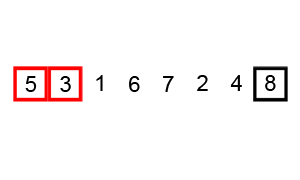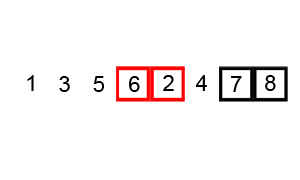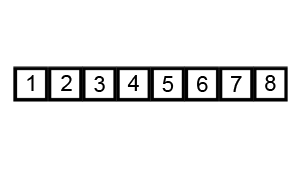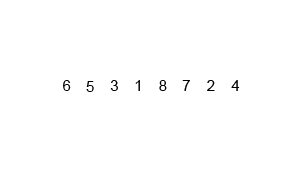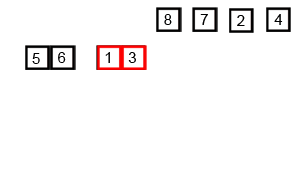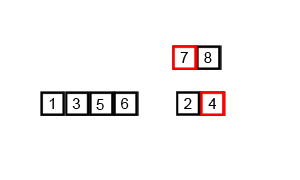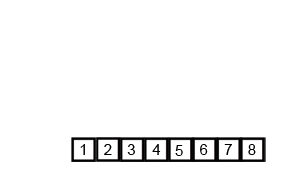【排序算法】插入+选择+交换+归并+基数+C代码实例
*基数排序中,n代表待排序的元素个数,d个关键码(最高数位,比如12最大的话,为2),关键码的取值范围为r(比如0~9,为10)
目录
一、插入排序
1.直接插入
2.希尔插入
二、选择排序
1.简单选择
2.堆选择
三、交换排序
1.冒泡排序
2.快速排序
四、归并排序
五、基数排序
一、插入排序
1.直接插入
插入排序的基本思想:将一个记录插入到已经排序好的有序表中,
即是说,要插入到有序表中,比key元素小的元素(a[ i ]
时间复杂度:O(n^2),因为2层循环嘛
空间复杂度:O(1),因为没有用到任何辅助数组
void myinsertsort(vector &v,int gap=1) {
for (int j = gap; j < v.size(); j++) {
int key = v[j];
int i = j - gap;
while (i >= 0 && v[i] > key) {
v[i + gap] = v[i];
i-= gap;
}
v[i + gap] = key;
}
}
int main() {
vector v = { 3,10,2,11,1,12,0,13 };
myinsertsort(v);
for (const auto&p : v) {
cout << p << " ";
}
cout << endl;
} 直接插入的简单gif实例:
*红色框就是key元素,黑色框就是有序表,可以看到直接插入算法就是将一个记录(key)插入到已经排序好的有序表中
2.希尔插入
希尔插入和插入排序很像,区别在于
刚开始的gap是数组长度的二分之一,之后循环gap=gap/2
再某些情况下,希尔插入会非常有效,比如当数组为{ 11,12,13,1,2,3 },
gap=3时,就足够将整个数组进行排序
gap=1时,就不会有任何交换或者插入的操作,会节省很多时间
时间复杂度:O(n^1.3),这是平均情况,最坏情况也是O(n^2),具体计算的方式暂时没有搞懂
空间复杂度:O(1),因为没有用到任何辅助数组
void mysellsort(vector &v) {
for (int i = v.size() / 2; i >= 1; i/=2) {
myinsertsort(v, i);
cout << i << endl;
for (const auto&p : v) {
cout << p << " ";
}
cout << endl << endl;
}
}
int main() {
//vector v = { 3,10,2,11,1,12,0,13 };
vector v = { 11,12,13,1,2,3 };
mysellsort(v);
for (const auto&p : v) {
//cout << p << endl;
cout << p << " ";
}
cout << endl;
} 比较直观的希尔排序过程:
希尔排序的gif实例:
*相同颜色代表是同一个组
二、选择排序
1.简单选择
基本思想:不断的在无序表中选择一个最小的,记录在k中,也就是 if(v[j]
时间复杂度为O(n^2),因为是2层循环
void myselectSort(){
for(int i=0;i
2.堆选择
所谓完全二叉树,
深度为k的完全二叉树,至少有2^(k-1)个节点,至多有2^k-1个节点。所谓深度,即层数。
最后一层若未铺满,则都连续集中在最左边,
如下就是一颗完全二叉树,深度为4
堆排序,把数组序列,看成,完全二叉树的层序遍历序列!!!
比如序列{ a b c d e },长度为5
会被直接看成
a
/ \
b c
/ \
d e
紧接着需要定位到最末一个具有子节点的节点,比如b,
当然,程序中从floor(5/2)=2开始,也就是c,但是因为2*2+1<5不成立,直接跳出while循环,所以实际上是从b开始的
在堆排序中,child=2*par+1 这个可以理解为层序遍历序列的规则!已知par,那么child的位置一定是 2*par+1
这个child如果大于兄弟节点,则++child,确保child是子节点中最大的节点的索引。
child和par节点比较,如果比par大,则直接执行"交换par和child"+"更新par和child",否则跳出循环!
因为,buid这个完全二叉树的时候,是从自底向上build的;
而且,在后面adjust的时候,如果child节点小于par节点,代表child的子节点也都小于现在的par节点,
所以,直接跳出循环!
堆排序的build,就是将原来无序的数组,变成,大顶堆的层序遍历序列(大顶堆就是堆顶的元素最大)
后面在选择的时候就直接选择堆顶元素(数组的0),并将其与最末端的元素交换
交换之后就控制整体的需要重新adjust的范围了,所以程序上是for (int i = v.size() - 1; i >= 0; i--)
for (int i = v.size() - 1; i >= 0; i--) {
int t = v[0]; v[0] = v[i]; v[i] = t;
heapadjust(v,0, i);
}堆排序就分为三个部分:build、adjust、sort
- build的部分注意adjust从floor(n/2)开始,范围是全范围(自底向上让数组符合完全二叉树大顶堆的层序遍历序列)
- adjust的部分注意child=2*par+1,用来确定子节点的索引,同时根据子节点们的对比,适当++child
- sort的部分注意起始端和末端互换,不断缩小范围
时间复杂度:![]()
void heapadjust(vector &v,int par, int length) {
int child = 2 * par + 1;
while (child &v) {
for (int i = v.size() / 2; i >= 0; i--) {
heapadjust(v,i, v.size());
}
}
void myheapsort(vector &v) {
buildheap(v);
for (int i = v.size() - 1; i >= 0; i--) {
int t = v[0]; v[0] = v[i]; v[i] = t;
heapadjust(v,0, i);
}
} 堆排序的一个简单gif实例{5,2,7,3,6,1,4} :
build的过程用树来可视化是很形而上的,实际上是把数组序列看成,完全二叉树的层序遍历序列!!!
三、交换排序
1.冒泡排序
0到小于n-1,等于遍历了n-1个数(0,1,2,...,n-2)
对于n个元素,冒泡的第二层循环起码交换n-1次(比如,4个元素,起码遍历3次,之后依次递减遍历次数)
之后每一个第二层循环都会沉淀++,所以要 - i (因为i是会递增的)
void mybubblesort(vector&v) {
int n = v.size();
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1 - i; j++) {
if (v[j] > v[j + 1]) {
int t = v[j]; v[j] = v[j+1]; v[j+1] = t;
}
}
}
} 冒泡排序的简单gif实例:
2.快速排序
part函数的作用就是让low索引的元素找到[low,high]范围中的中值的位置t,
并且t的左边的元素都比t元素小,t右边的元素都比t元素大(简称,左小右大)
排序的问题就分解为:
1.找到[low,high]范围中的中值的位置,并且数组分为左小右大两个数组
2.递归的缩小问题的范围,[low,t-1] 和 [t+1,high]
int part(vector &v, int low, int high) {
int t = v[low];
while (low < high) {
while (lowt)--high;
v[low] = v[high];
while (low < high&&v[low] < t)++low;
v[high] = v[low];
}
v[low] = t;
return low;
}
void myquicksort(vector&v,int low,int high) {
if (low < high) {
int t = part(v, low, high);
myquicksort(v, low, t - 1);
myquicksort(v, t + 1, high);
}
}
int main() {
vector v = { 3,1,5,7,2,4,9,6,10,8 };
myquicksort(v, 0, v.size() - 1);
for (const auto&p : v) {
cout << p << " ";
}
cout << endl;
}
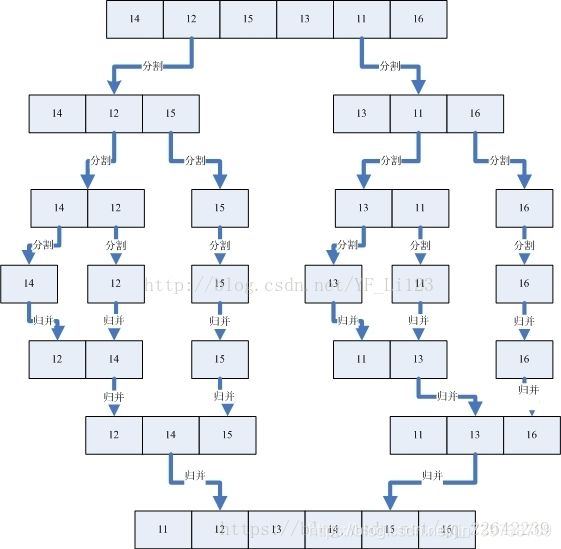
四、归并排序
//分解:索引的分解数列拆分至单个。。。
拆分的计算范式是:递去
遇到low不小于high的情况则返回,所以要设置if (low < high)
void mymergesort(vector&v, int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
mymergesort(v, low, mid);
mymergesort(v, mid + 1, high);
merge(v, low, mid, high);
}
} //合并:然后2个单个合并为一双,两个一双或者一双和单个合并,。。。
合并的计算范式是:归来
合并的过程中需要用到中间数组tmp,利用它进行存放临时的合并结果
合并的过程就是遍历[low<=i <= mid]和[mid+1<=j <= high]的过程
比较这两个范围中的数哪一个更小,就会优先存放在tmp中,
最后将tmp拷贝至v[low <= high]中,即可完成合并
时间复杂度:![]()
void merge(vector&v, int low, int mid, int high) {
//vector tmp(high - low + 1);
int* tmp = new int[high - low + 1];
int i = low;
int j = mid + 1;
int k = 0;
while (i <= mid&&j <= high) {
if (v[i] < v[j]) {
tmp[k++] = v[i++];
}
else {
tmp[k++] = v[j++];
}
}
while (i <= mid) {
tmp[k++] = v[i++];
}
while (j <= high) {
tmp[k++] = v[j++];
}
k = 0;
while (low <= high) {
v[low++] = tmp[k++];
}
}
void mymergesort(vector&v, int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
mymergesort(v, low, mid);
mymergesort(v, mid + 1, high);
merge(v, low, mid, high);
}
}
int main() {
vector v={ 3,1,5,7,2,4,9,6,10,3 };
mymergesort(v, 0, v.size() - 1);
for (const auto&p : v) {
cout << p << endl;
}
cout << endl;
} 另外一个比较直观的归并排序实例:
归并排序的简单gif实例:
五、基数排序
基数排序不需要比较关键字的大小。
- 计数表和记位表count
一开始用来记当前基数下的编号0~9的计数,后面采用逐项累加的方法,记住每个桶位置边界(最右)
- 将元素放入临时数组容器(tmp),要从右往左依次扫描,保证排序的稳定
因为count记录的是桶的最右位置边界,而且基数排序默认从左往右递增(0~9),
比如,0,10,3,13,刚开始分成两桶左(0,10)和右(3,13)
进入更高数位时,0,3分为一桶,这时按照从右往左扫描数组,并放入所属桶的最右边界处,才是正确的,
如果按照从左往右扫描,那么前面一轮循环的基数排序信息没有起到任何作用,甚至会造成混乱
- 最后,将tmp拷贝到数组中,每个循环执行一次
- 最后的最后,radix*=10,对更高数位进行基数排序
设待排序列为n个元素,d个关键码(最高数位,比如12最大的话,为2),关键码的取值范围为r(0~9,为10个),
时间复杂度:O(d(n+r)),大循环d,中间夹着两个分别时n和r的循环,分别用于计数和拷贝tmp
空间复杂度:O(dr+n),需要d个空间为r的数组存放count,需要1个空间为n的数组暂存tmp
int maxbit(vector&v) {
int d = 1;
int p = 10;
for (int i = 0; i < v.size(); i++) {
if (v[i] > p) {
p *= 10;
d++;
}
}
return d;
}
void myradixsort(vector&v) {
int* count = new int[10];
int* tmp = new int[v.size()];
int radix = 1;
int d = maxbit(v);
int i, j, k;
for (i = 1; i <= d; i++) {
for (j = 0; j < 10 ; j++) {
count[j] = 0;
}
for (j = 0; j < v.size(); j++) {
count[(v[j] / radix) % 10]++;
}
for (j = 1; j < 10; j++) {
count[j] = count[j - 1] + count[j];
}
for (j = v.size() - 1; j >= 0; j--) {
k = (v[j] / radix) % 10;
tmp[count[k] - 1] = v[j];
count[k]--;
}
for (j = 0; j < v.size(); j++) {
v[j] = tmp[j];
}
radix *= 10;
}
}
int main() {
vector v = { 73, 22, 93, 43, 55, 14, 28, 65, 39, 81 };
//vector v = { 3,1,5,7,2,4,9,6,10,31 };
myradixsort(v);
for (const auto&p : v) {
cout << p << endl;
}
cout << endl;
}
本文对八大排序算法进行了整理和总结,后续还会对某个排序算法进行深入的研究和拓展,
比如冒泡排序实际上还有很多种扩展方法、简单选择排序也可以变成双向选择等等,这就是后话了!