R_差值_拟合_回归_样条

双十一活动还在持续热销中，全场五折等你来！

点击图片，查看课程详情

作者：李誉辉 四川大学在读研究生  

1 概念辨析

因为误差的存在，很多时候，直接对数据点进行连线没有意义，不能清楚的反映其中的变量关系，这时候就需要数据拟合或者线性回归，
现实中，很多人都搞不清线性拟合和线性回归，加上差值和样条曲线，更是让人感觉混乱。
本文中，将带大家辨析这些概念之间的关系，并与ggplot2绘图结合进行展示。

1.1 差值

对于一组数据点，那么理论上一定存在可以通过这几个点的多项式，通常数据点越多，多项式阶数约高，这个求多项式的过程就叫差值。
但是计算机存在计算精度和误差累计，在多项式阶数过高的，通常7,8阶左右，就会出现龙格现象(Runge phenomenon)， 这种现象导致数据点两端的差值偏差极大，根本没法看。 所以通常差值不会超过7，
但是现实中，数据点成百上千很正常，所以通过对数据点分段，分段进行低阶差值，就能避免龙格现象。

1.2 拟合与回归

实际中，实验测定或者统计获得的数据也是存在实验误差或者统计误差的，所以差值的方法并不实用，这就需要拟合了，
拟合就是求一条曲线，使得该曲线与数据点的趋势最接近，与差值的区别在于，拟合的曲线并不一定过数据点。 拟合中，最常用的线性拟合，但是拟合出的曲线并不一定非得是直线，通过数据变换，线性拟合也能拟合出曲线。

1.2.1 线性拟合：

• 超过2组数据点，求1次函数ax + b = 0，使得残差的绝对值和最小
  

• 残差：观测值(yi)与预测值(axi + b)之差，为了方便计算，通常求残差的平方和最小
  

• 计算方法：设定未知数，a和b,然后计算残差，残差平方和为a和b的表达式，对残差平方和求偏导，
  设偏导均为0，得到2个a和b的2元方程，即可解出a和b的值。

1.2.2 线性回归：

• 线性回归是通过“极大似然估计方法”得到的，是统计学中抽样的方法得到的
  得出的线性方程的系数与线性拟合相同，但是计算思路不同，误差判定方式不同

1.2.3 线性最小二乘法：

• 线性最小二乘法与线性拟合不同的是，不是通过残差计算的，同样设定未知量a和b,
  然后带入xi和yi组成一个超顶线性方程组，其方程的个数大于未知数的个数， 设系数矩阵为A，x = t(c(a, b))为未知量矩阵，则Ax = b
  两边同时左乘A的转置矩阵，变成t(A) %*% A %*% x = t(A) %*% b，首先计算t(A) %*% A和t(A) %*% b，
  因为t(A) %*% A为2阶矩阵，所以很可能有唯一解，该解与残差平方和最小一致

1.3 样条曲线

样条差值是分段低阶差值的一种， * 2次样条：在每2个点之间求2阶多项式，并使多项式在得观测点处一阶光滑(一阶导数连续，即存在二阶导数)
* 3次样条：在每2个点之间求3阶多项式，并使多项式在得观测点处二阶光滑(二阶导数连续，即存在三阶导数)
给定2个边界条件，即可求得唯一的样条差值多项式
边界条件分为3类： * 2个端点处的一阶导数值
* 2个端点处的二阶导数值
* 对于周期性数据，则是两个端点处函数值相等，且给定端点处1阶导数值或2阶导数值

2 函数应用

接下来通过函数对假想的数据点进行拟合、差值、线性回归等分析。

2.1 多项式差值与拟合

pracma包是一个科学计算的包，有很多现成的函数可以使用。使用install.packages("parcma")可以安装。
关键函数：
* polyfit(x, y, n) 产生多项式系数,幂次由高到低, n < (length(x)-1)则自动拟合数据
* polyfix(x, y, n, xfix, yfix) 同样是参数多项式系数，参数xfix，yfix表示参考点坐标，即保证拟合曲线一定过该点
* polyval(p, x) 根据多项式系数向量P,产生多项式，然后根据该多项式计算x坐标的的值：

library(pracma)
library(ggplot2)

set.seed(1)
x <- seq(0, pi, length.out = 25)
y <- sin(x) + 0.05 * runif(length(x), -2, 2)
p1 <- polyfit(x, y, 6)  # 拟合6阶多项式,返回长度为7的向量
p2 <- polyfix(x, y, 6, xfix = c(1, 3), yfix = c(0.75, 0.05))
p3 <- polyval(p1, x)

data1 <- data.frame(x = x, y = p3, y_fix = polyval(p2, x), y_point = y, stringsAsFactors = F)
g1 <- ggplot(data1) + geom_line(aes(x, y), color = "pink", size = 1) + geom_line(aes(x, 
    y_fix), color = "blue", size = 1) + geom_point(aes(x, y_point), color = "grey", 
    size = 3)
g1

2.2 线性回归lm()

介绍几个线性回归（linear regression）中的术语：
* 残差（Residual）: 基于回归方程的预测值与观测值的差。
* 离群点（Outlier）: 线性回归（linear regression）中的离群点是指对应残差较大的观测值。 也就是说，当某个观测值与基于回归方程的预测值相差较大时，该观测值即可视为离群点。 离群点的出现一般是因为样本自身较为特殊或者数据录入错误导致的，当然也可能是其他问题。
* 杠杆率（Leverage）: 当某个观测值所对应的预测值为极端值时，该观测值称为高杠杆率点。
杠杆率衡量的是独立变量对自身均值的偏异程度。高杠杆率的观测值对于回归方程的参数有重大影响。
* 影响力点：（Influence）: 若某观测值的剔除与否，对回归方程的系数估计有显著相应，则该观测值是具有影响力的，称为影响力点。 影响力是高杠杆率和离群情况引起的。 * Cook距离（Cook’s distance）: 综合了杠杆率信息和残差信息的统计量。

2.2.1 一元线性回归 lm()

# 线性回归,建立x与y之间的线性关系
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

relation <- lm(y ~ x)  # 建立线性关系
print(relation)  # 查看关系系数

print(relation[[1]][1])  # 提取关系系数
print(relation[[1]][2])

result <- predict(relation, data.frame(x = 170))  # 根据关系系数预测x=170时的y值
print(result)

2.2.1.1 多元回归lm()

 线性回归,建立x与y之间的线性关系
input <- mtcars[, c("mpg", "disp", "hp", "wt")]
head(mtcars)

model <- lm(mpg ~ disp + hp + wt, data = input)  # 建立模型，参数data表示输入数据
print(model)

# 索引相关系数
a <- coef(model)[1]
Xdisp <- coef(model)[2]
Xhp <- coef(model)[3]
Xwt <- coef(model)[4]

# 生成多元回归方程
fun_mpg <- function(x1, x2, x3) {
    mpg <- a + Xdisp * x1 + Xhp * x2 + Xwt * x3
    return(mpg)
}

# 根据回归方程进行预测
fun_mpg(221, 102, 2.91)

2.3 线性拟合

步骤： * 首先是数据预处理(包括剔除异常值，数据规范化：去除单位，减去最小值，除以最大值，使数据在(0, 1)区间内)
* 然后是画散点图，根据点的分布，建立函数关系(不一定是线性函数)
* 然后根据该函数关系，推导出线性函数关系
* 根据该线性函数关系，进行线性拟合，解出相关系数，将解带入原函数，绘函数图像

2.3.1 利用数据变换进行数据拟合

因为线性拟合的步奏比较多，线性回归结果一样， 所以代码中直接使用线性回归代替，但数据变换过程才是关键，也是线性拟合可以拟合出曲线的关键。

library(pracma)
library(ggplot2)
set.seed(11)
black <- function(x) {
    2 * x * exp(0.5 * x) + runif(length(x), min = -1, max = 1)
}
x_test <- seq(0, 5, 0.2)
y_test <- black(x_test)

rigion <- data.frame(x = x_test, y = y_test)  # 预处理后的数据
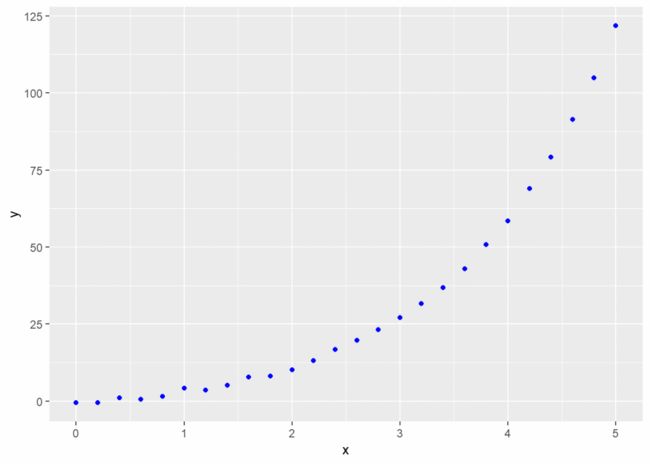
ggplot(rigion, aes(x, y)) + geom_point(color = "blue")  # 画散点图，从图中可以建立指数函数模型
# 函数模型：y = c1*t*exp(c2*t), 函数线性化：lny = lnc1 + lnt + c2*t
# 替换变量,将未知量成为线性函数的系数：lny -lnt = c2*t + k,
# 自变量为t,因变量为lny-lnt,求系数 线性拟合求：k, c2
fun_y <- log(y_test, base = exp(1)) - log(x_test, base = exp(1))
fun_x <- x_test
relation <- lm(fun_y ~ fun_x)  # 建立线性关系
print(relation)  # 查看关系系数，结果c2 = 0.5583, k = 0.4780
k <- relation[[1]][1]
c2 <- relation[[1]][2]

# 带入c2和k的值，求出c1 = e^k
c1 <- exp(k)
# 函数模型为：
fun_last <- function(x) {
    c1 * x * exp(c2 * x)
}
# 绘拟合后的图形
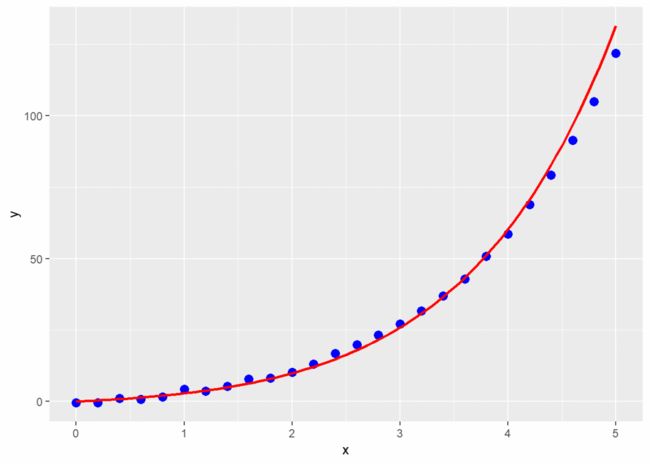
ggplot(rigion, aes(x, y)) + geom_point(color = "blue", size = 3) + stat_function(fun = fun_last, 
    color = "red", size = 1)

2.3.2 利用curvefit()函数拟合曲线

同样来自pracma包
curvefit(u, x, y, n, U = NULL, V = NULL)
参数解释：
* x, y表示要拟合的数据点坐标
* u 表示拟合曲线要经过点的x坐标，即返回该点的y坐标
* n 表示要拟合的多项式阶数 返回：4个元素的列表，分别是拟合曲线的x,y坐标xp,yp; 和拟合多项式系数,px,py

library(pracma)
library(ggplot2)
set.seed(21)
u <- seq(0, pi, length.out = 50)
x <- cos(u) + 0.005 * sample(-5:5, 50, replace = T)
y <- sin(u) + 0.005 * sample(-5:5, 50, replace = T)

myfit <- curvefit(u, x, y, n = 5)  # 5阶多项式拟合
str(myfit)  # 4个元素的列表，分别是拟合曲线的x,y坐标xp,yp; 和拟合多项式系数,px,py

xfit <- unlist(myfit$xp)
yfit <- unlist(myfit$yp)
x[length(xfit)] <- NA
y[length(xfit)] <- NA
df_fit <- data.frame(x = x, y = y, xfit = xfit, yfit = yfit)
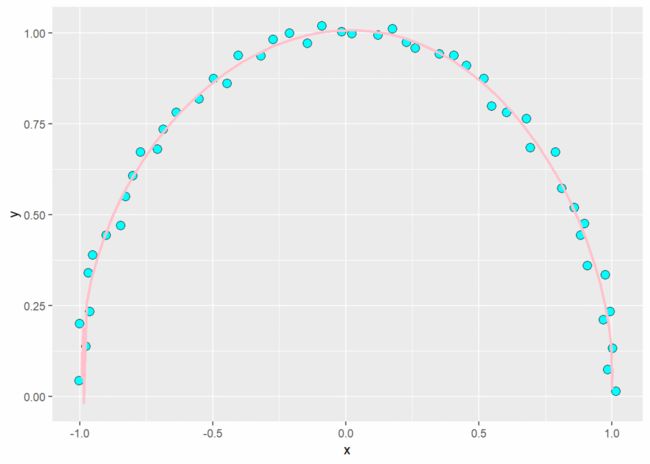
ggplot(df_fit) + geom_point(aes(x = x, y = y), shape = 21, size = 3, fill = "cyan") + 
    geom_line(aes(x = xfit, y = yfit), color = "pink", size = 1)

2.4 样条曲线

方法：
* 方法一，利用spline函数生成平滑数据，然后利用绘图函数绘制平滑曲线
* 方法二，使用ggplot2扩展包ggalt中的geom_xspline()或stat_xspline()函数，自动绘制平滑曲线

语法：
spline(x, y = NULL, n = 3*length(x), method = "fmm", xmin = min(x), xmax = max(x), xout, ties = mean) 参数解释：
* x，y 分别表示x轴和y轴坐标向量
* n 表示要输出的点的数量，默认为3倍输入
* xmin 表示指定向量开始差值的点的x坐标
* xmax 表示指定向量结束差值的点的x坐标 语法：

geom_xspline(mapping = NULL, data = NULL, stat = "xspline",
  position = "identity", na.rm = TRUE, show.legend = NA,
  inherit.aes = TRUE, spline_shape = -0.25, open = TRUE,
  rep_ends = TRUE, ...)

参数解释：
* spline_shape 在(-1, 1)区间内的数字，表示控制端点的参数
* rep_ends 表示端点重复，生成多周期

library(ggplot2)
timeline <- read.csv(file = "E:/resources_reserved/文档/R语言/自编教程/timeline.csv", header = T, skip = 1) # 读取刚刚下载的文件
sp1 <- spline(timeline$year, timeline$count, n = 10000) # 
str(sp1)

xl <- as.vector(sp1$x); yl <- as.vector(sp1$y)
length(xl)
str(timeline)
xp <- timeline$year; yp <- timeline$count
xp[length(xl)] <- NA; yp[length(xl)] <- NA
newdf <- data.frame(xl = xl, yl = yl, xp = xp, yp = yp) # 合并原始数据和样条差值后的数据，NA补齐
str(newdf)

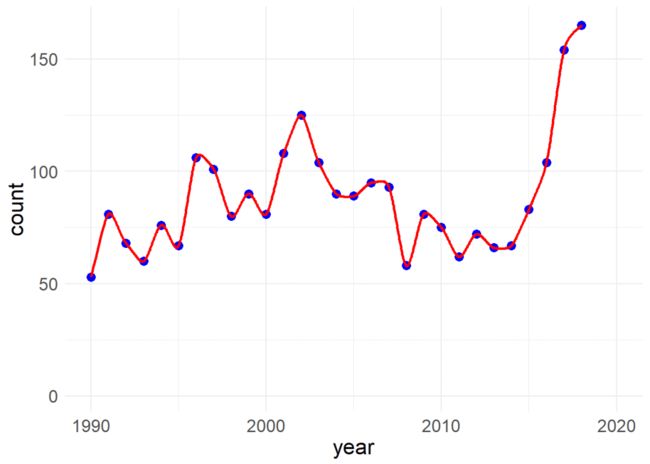
ggplot(newdf) + 
  geom_point(aes(x = xp, y = yp), color = "blue", size = 3) +
  geom_smooth(aes(x = xl, y = yl), color = "red", size = 1) +
  xlim(1990, 2020)

# 方法2，使用ggalt扩展包:不需要整合长度不一样的数据
library(ggalt)
ggplot(timeline,aes(year,count))+ 
  geom_point(color='blue', size=3)+
  geom_xspline(spline_shape = -0.4, size=1, col='red')+ # 端点控制不重要，反正这儿只截取中间一部分图像
  xlim(1990,2020)+
  theme_minimal()+ 
  theme(text=element_text(size=17))

# 两种方法结果不一样，第一种是伪样条曲线，是用差值函数生成曲线上的点，然后用点绘图，
# 第二种是在数据点之间计算样条函数，然后通过函数绘制图像 

2.4.1 三次样条差值

同样来自pracma包
cubicspline(x, y, xi = NULL, endp2nd = FALSE, der = c(0, 0)) 返回xs处y坐标
参数解释：
* x,y表示要差值的点的坐标，x和y为等长的向量
* xi 表示样条曲线要经过的点的坐标，函数即返回在该点y坐标
* endp2nd 为逻辑值，表示是否指定边界条件，TRUE则将der参数作为边界条件(端点处导数)
* der 表示指定边界条件(端点处导数)

library(pracma)
library(ggplot2)
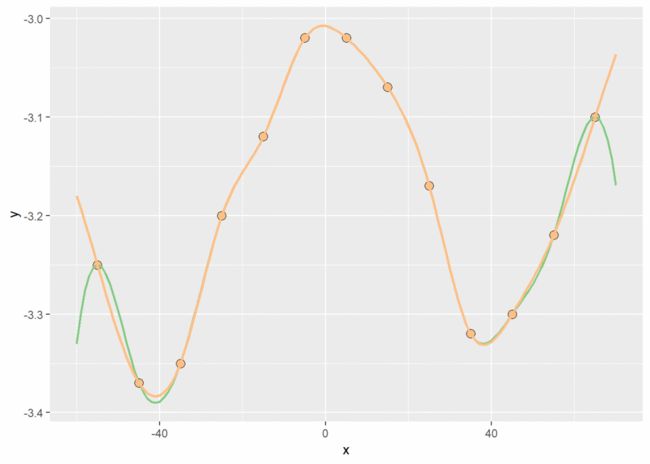
x <- seq(-55, 65, by = 10)
y <- c(-3.25, -3.37, -3.35, -3.20, -3.12, -3.02, -3.02, -3.07, -3.17, -3.32, -3.30, -3.22, -3.10)
xs <- seq(-60, 70, by = 1) # 序列步长很小，便于绘制曲线

ys1 <- cubicspline(x, y, xs, endp2nd = TRUE)     # 默认边界条件，导数均为0，返回x=xs的y坐标
ys2 <- ys <- cubicspline(x, y, xs) # 不指定边界条件

x[length(xs)] <- NA; y[length(xs)] <- NA

df_splines <- data.frame(x = x, y = y, xs = xs, ys1 = ys1, ys2 = ys2)
ggplot(df_splines) + 
  geom_point(aes(x, y), shape = 21, size = 3, fill = "#fdc086") + 
  geom_line(aes(x=xs, y=ys1), color = "#7fc97f", size = 0.8) + # 默认边界条件，端点处导数为0
  geom_line(aes(x=xs, y=ys2), color = "#fdc086", size = 1) # 无边界条件

今日

推荐

R语言可视化 5折优惠等着你 扫描 下图二维码 即可学习 点击 阅读原文 加入SVIP可免费学习