CS231n Spring 2019 Assignment 2—Batch Normalization

---

上一次我们完成了任意多层的全连接神经网络的设计，并且学习了一些改进的优化方法，这是使网络更容易训练的一个思路，另一个思路就是Batch Normalization(批量归一化)，出自2015年的论文：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift，这使得深层网络训练变得更加容易。课程中涉及到的主要是lecture 7，要完成的就是BatchNormalization.ipynb这一个作业，但是里面会有一点额外的layer normalization的编写，类似于batch normalization。

Batch normalization

要理解batch normalization的话，还是得看一下上面的那篇论文，这样对它的前向和反向传播会理解更好，并且知道Batch normalization主要是用来解决什么问题，网上类似的介绍也有很多，推荐几篇之前自己看的认为写的比较好的：

• 【深度学习】深入理解Batch Normalization批标准化，这个的话看一下它宏观的介绍即可，具体还是看教程视频及slide，加上ipynb里面的编程提示就行
• 知乎深度学习中 Batch Normalization为什么效果好？
• 李宏毅老师对于Internal Covariate Shift有个很形象的比喻

可以先粗略地看一遍论文，看完论文再看上面几篇博客就能够有大致的认识了（网上大多都是互相借鉴的，看两篇高质量的就不用再多看了），在这里也分享几点几点自己的认为比较重要的吧(之后有更多理解再来补充)：

1. batch normalization在训练阶段和测试阶段是不一样的，训练阶段计算的是每一个batch的均值和方差，但是测试时用的是训练后的滑动平均（我理解也就是一种加权平均）的均值和方差
2. batch normalization确实有很多优点，如使得更深的网络更容易训练，改善梯度传播，允许更大的学习率使得收敛更快，使得对初始化不是那么的敏感 ；但是实际中我们batch size是受硬件条件限制的，像我们这种穷人batch size肯定不会很大，这样的话batch normalization的作用不是那么明显
3. batch normalization也有1D和2D之分，甚至3D都有（在pytorch里都有定义），其中1D叫作Temporal Batch Normalization；2D叫作Spatial Batch Normalization；3D叫作Volumetric Batch Normalization or Spatio-temporal Batch Normalization（见下图）
4. 归一化出来的并不一定是以0为均值，以1为方差；有scale系数$\gamma$和shift系数$\beta$之后，实际上是以$\beta$为均值，以$\gamma$为方差

forward

前向传播时，每个 mini-batch 的数据都用自己的均值方差来标准化，然后在训练的过程中，会计算一个 running_mean 和 running_var，以便预测的时候用（教程中也提到这一块与论文中的做法是有一些差别的）。这里也放一下论文中前向传播的图片：
batchnorm_forward(x, gamma, beta, bn_param)—>return out, cache

def batchnorm_forward(x, gamma, beta, bn_param):
   # 因篇幅缘故，把注释提示删除了
    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    if mode == 'train':
        
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        sample_mean = np.mean(x, axis = 0)
        sample_var = np.var(x, axis = 0)
        x_hat = (x - sample_mean) / (np.sqrt(sample_var + eps))
        out = gamma * x_hat + beta
        cache = (gamma, x, sample_mean, sample_var, eps, x_hat)
        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        #######################################################################
        #                           END OF YOUR CODE                          #
        #######################################################################
    elif mode == 'test':
        #######################################################################
        # TODO: Implement the test-time forward pass for batch normalization. #
        # Use the running mean and variance to normalize the incoming data,   #
        # then scale and shift the normalized data using gamma and beta.      #
        # Store the result in the out variable.                               #
        #######################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        x_hat = (x - running_mean) / (np.sqrt(running_var + eps))
        out = gamma * x_hat + beta
        # no cache for test-time.As it's no BP process.

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        #######################################################################
        #                          END OF YOUR CODE                           #
        #######################################################################
    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache

backward

反向传播中需要写两个版本的函数：batchnorm_backward 是用计算图的方式计算的，而后面那个 batchnorm_backward_alt 是用论文里的公式直接实现的，我自己虽然学习了之前计算图那节教程，现在一实操，发现还是只会写一些简单gate的反向传播，对于这个batch normalization就懵了（虽然花时间尝试画，但还是不会画），后来找到一篇讲batch normalization用计算图反向传播的比较高质量的博客，我这里直接放一下它画的计算图，它里面也有一步一步教怎么反向推导：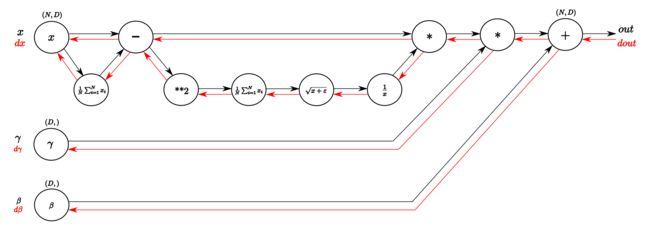
这样就可以完成batchnorm_backward函数，我基本也就是照着他写的：
batchnorm_backward(dout, cache)—>return dx, dgamma, dbeta

def batchnorm_backward(dout, cache):
    """
    Backward pass for batch normalization.

    For this implementation, you should write out a computation graph for
    batch normalization on paper and propagate gradients backward through
    intermediate nodes.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from batchnorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None
    ###########################################################################
    # TODO: Implement the backward pass for batch normalization. Store the    #
    # results in the dx, dgamma, and dbeta variables.                         #
    # Referencing the original paper (https://arxiv.org/abs/1502.03167)       #
    # might prove to be helpful.                                              #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    # More info about backpropogation in BN,see:
    # https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html
    gamma, x, sample_mean, sample_var, eps, x_hat = cache
    N, D = dout.shape

    dbeta = np.sum(dout, axis=0)

    dgammax = dout #not necessary, but more understandable
    dgamma = np.sum(dgammax * x_hat, axis=0)

    dxhat = dgammax * gamma
    xmu = x - sample_mean
    divar = np.sum(dxhat*xmu, axis=0)
    ivar = 1 / (np.sqrt(sample_var + eps))
    dxmu1 = dxhat * ivar
    dsqrtvar = -1. / ((np.sqrt(sample_var + eps))**2) * divar
    dvar = 0.5 * 1. /np.sqrt(sample_var+eps) * dsqrtvar
    dsq = 1. /N * np.ones((N,D)) * dvar
    dxmu2 = 2 * xmu * dsq
    dx1 = (dxmu1 + dxmu2)
    dmu = -1 * np.sum(dxmu1+dxmu2, axis=0)
    dx2 = 1. /N * np.ones((N,D)) * dmu
    dx = dx1 + dx2

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################

    return dx, dgamma, dbeta

而这个batchnorm_backward_alt就要参照论文的公式写了，两者运算速度差不多，有时候第一种还更快一点点：

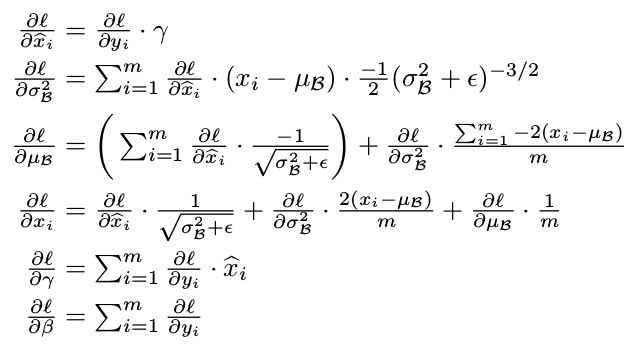
batchnorm_backward_alt(dout, cache)—>return dx, dgamma, dbeta

def batchnorm_backward_alt(dout, cache):
    """
    Alternative backward pass for batch normalization.

    For this implementation you should work out the derivatives for the batch
    normalizaton backward pass on paper and simplify as much as possible. You
    should be able to derive a simple expression for the backward pass. 
    See the jupyter notebook for more hints.
     
    Note: This implementation should expect to receive the same cache variable
    as batchnorm_backward, but might not use all of the values in the cache.

    Inputs / outputs: Same as batchnorm_backward
    """
    dx, dgamma, dbeta = None, None, None
    ###########################################################################
    # TODO: Implement the backward pass for batch normalization. Store the    #
    # results in the dx, dgamma, and dbeta variables.                         #
    #                                                                         #
    # After computing the gradient with respect to the centered inputs, you   #
    # should be able to compute gradients with respect to the inputs in a     #
    # single statement; our implementation fits on a single 80-character line.#
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    # Because no backprop in test mode
    gamma, x, sample_mean, sample_var, eps, x_hat = cache
    M = x.shape[0]

    dgamma = np.sum(x_hat * dout, axis = 0)
    dbeta = np.sum(dout , axis = 0)
    
    dx_hat = dout * gamma
    dvar = np.sum(dx_hat * (x - sample_mean) * (-0.5) * np.power(sample_var + eps, -1.5), axis = 0)
    dmean = np.sum(dx_hat * -1 / np.sqrt(sample_var +eps), axis = 0) + dvar * np.mean(-2 * (x - sample_mean), axis =0)
    dx = 1 / np.sqrt(sample_var + eps) * dx_hat + dvar * 2.0 / M * (x-sample_mean) + 1.0 / M * dmean


    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################

    return dx, dgamma, dbeta

Fully Connected Nets with Batch Normalization

这时可以在上次任意多层之间的ReLU层前加上Batch Normalization层了，可以把之前的pass位置取代掉，这在我之前一篇中其实已经放上去了，需要注意的一点是最后一层是不需要加Batch Normalization的。

之后会对比有无Batch Normalization层效果，来检验一下Batch Normalization是否有作用，并且探寻了一下与weight initialization、batch size之间的关系，这在下面的结果图里都可以直观地看到。

Layer normaliztion

Layer Normalization是Hiton团队在2016年提出的，Batch Normalization主要会受硬件限制，而Layer Normalization不再是对batch进行归一化，而是对features进行归一化，所以没有了batch size的限制，而且它的训练与测试阶段是同样的计算行为，可以用在循环神经网络中：

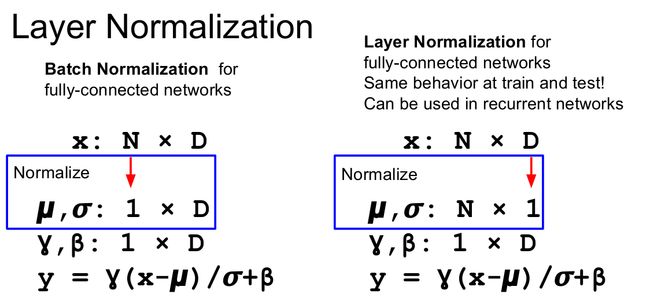
其实还有2017年提出的Instance Normalization: The Missing Ingredient for Fast Stylization和2018年提出的Group Normalization，可以通过下面这张图帮助理解：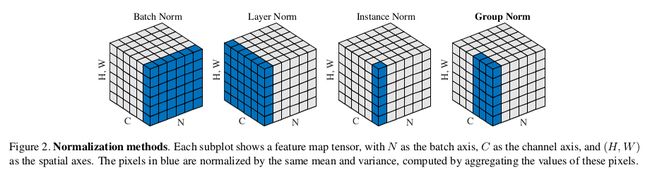
也可以看这一篇的总结

forward

总之还得来完成作业：这里前向传播跟Batch Normalization只是计算沿着的轴改变了一下，基本思路是一样的，在算完均值和方差的时候reshape了一下，否则shape会变成[1,N]，而不是我们想要的[N,1]：
layernorm_forward(x, gamma, beta, ln_param)—>return out, cache

def layernorm_forward(x, gamma, beta, ln_param):
    """
    Forward pass for layer normalization.

    During both training and test-time, the incoming data is normalized per data-point,
    before being scaled by gamma and beta parameters identical to that of batch normalization.
    
    Note that in contrast to batch normalization, the behavior during train and test-time for
    layer normalization are identical, and we do not need to keep track of running averages
    of any sort.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - ln_param: Dictionary with the following keys:
        - eps: Constant for numeric stability

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    out, cache = None, None
    eps = ln_param.get('eps', 1e-5)
    ###########################################################################
    # TODO: Implement the training-time forward pass for layer norm.          #
    # Normalize the incoming data, and scale and  shift the normalized data   #
    #  using gamma and beta.                                                  #
    # HINT: this can be done by slightly modifying your training-time         #
    # implementation of  batch normalization, and inserting a line or two of  #
    # well-placed code. In particular, can you think of any matrix            #
    # transformations you could perform, that would enable you to copy over   #
    # the batch norm code and leave it almost unchanged?                      #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    sample_mean = np.mean(x, axis=1).reshape(-1, 1)
    sample_var = np.var(x, axis=1).reshape(-1, 1)
    x_hat = (x - sample_mean) / (np.sqrt(sample_var + eps))
    out = gamma * x_hat + beta
    cache = (gamma, x, sample_mean, sample_var, eps, x_hat)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return out, cache

backward

类似的，反向传播也可以“严重”参考batch normalization的反向传播代码，也就是计算均值方差的轴变了，注意现在都是1D的归一化：
layernorm_backward(dout, cache)—>return dx, dgamma, dbeta

def layernorm_backward(dout, cache):
    """
    Backward pass for layer normalization.

    For this implementation, you can heavily rely on the work you've done already
    for batch normalization.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from layernorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None
    ###########################################################################
    # TODO: Implement the backward pass for layer norm.                       #
    #                                                                         #
    # HINT: this can be done by slightly modifying your training-time         #
    # implementation of batch normalization. The hints to the forward pass    #
    # still apply!                                                            #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    gamma, x, sample_mean, sample_var, eps, x_hat = cache
    D = x.shape[1]
    
    dx_hat = dout * gamma
    dvar = np.sum(dx_hat * (x - sample_mean) * (-0.5) * np.power(sample_var + eps, -1.5), axis = 1)
    dmean = np.sum(dx_hat * -1 / np.sqrt(sample_var +eps), axis = 1) + dvar * np.mean(-2 * (x - sample_mean), axis =1)
    dvar = dvar.reshape(-1, 1)
    dmean = dmean.reshape(-1, 1)
    dx = 1 / np.sqrt(sample_var + eps) * dx_hat + dvar * 2.0 / D * (x-sample_mean) + 1.0 / D * dmean
    dgamma = np.sum(x_hat * dout, axis = 0)
    dbeta = np.sum(dout , axis = 0)
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dgamma, dbeta

结果

具体结果可见：BatchNormalization.ipynb，里面也有对问题的一些回答

链接

前后面的作业博文请见：

• 上一篇的博文：Fully-Connected Neural Nets(全连接神经网络)
• 下一篇的博文：Dropout