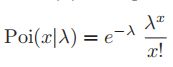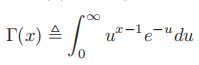Machine Learning——A Probabilistic Approach学习笔记 第二章 概率
第二章 概率(Probability)
2.1引言(Introduction)
- 在这一章,我们将会讲述关于概率论的更多细节。我们不会太过深入,但是我们至少会简要的了解一下我们在接下来的章节中所要涉及的思想。
- 让我们先来思考一下:什么是概率?
- 常见的解释有两种,第一种是frequentist解释。这种观点认为概率代表了一个事件发生的长期概率。例如,它对抛硬币的概率的解释是:如果抛很多次硬币,那么必然有一半左右是正面。另一种是贝叶斯解释,它认为概率是一种量化我们对事物的不确定性的认识。相比之下,它更加侧重信息表示而非重复试验。例如,它对抛硬币的解释则是:我们对硬币落下之后是正面或者反面的概率的期望相同。
- 贝叶斯解释的一个巨大的优势在于它可以被用来描述那些我们无法多次获取概率的事件。因此,我们在这本书中将会使用贝叶斯解释。好在,在不同的解释中,基本的概率论法则都是相同的,因此不会产生太大的影响。
2.2概率论初窥(a brief review)
这一部分是对于概率论的一个简单的介绍,为读者提供一个过渡。
2.2.1离散随机变量(discrete random variable)
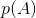 :A发生的概率,
:A发生的概率, :A不发生的概率=
:A不发生的概率= A=1:A是真的 A=0:A是假的
A=1:A是真的 A=0:A是假的- 我们可以通过定义一个离散随机变量X来延拓二元事件(即结果要么真要么假)的定义。X的取值范围可以是一个有限或可数无限集K。我们定义事件X=x的概率为
 ,或者简记为
,或者简记为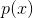 ,在这里p称为概率质量函数(probability mass function,简称pmf),其满足
,在这里p称为概率质量函数(probability mass function,简称pmf),其满足 ,且
,且
2.2.2基本法则
2.2.2.1两个事件同时发生的概率
2.2.2.2联合概率(joint probabilities)
- 联合事件:(乘法原理:product rule)
![]()
- 边际分布(marginal distribution):(加法原理:sum rule)
2.2.2.3条件概率
2.2.3贝叶斯法则
2.2.3.1举例:医学诊断
- 一个人想要用X光检测自己有没有得乳腺癌。已知乳腺癌的患病率是0.004,如果得了乳腺癌,那么X光检测阳性的几率是0.8;如果没有得,那么假阳性的几率则是0.1,那么,如果检测为阳性,她得乳腺癌的几率是?
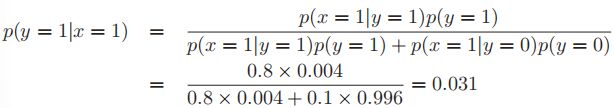
2.2.3.2举例:生成式分类器(generative classififier)
- 对上例的一般化:

- 这被称为生成式分类器,因为它规定(specify)了如何使用类条件密度(class conditional density)
 和类先验(class prior)
和类先验(class prior)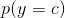 来获取信息。一个代替的方法是直接使用判别分类器求出(fit)类后验(class posterior)
来获取信息。一个代替的方法是直接使用判别分类器求出(fit)类后验(class posterior)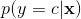
2.2.4独立和条件独立(conditional independence)
- 若有
 ,我们称X,Y无条件独立,记为
,我们称X,Y无条件独立,记为 ;一般地,如果集合里面的元素两两独立,我们也称其共同(mutal)独立
;一般地,如果集合里面的元素两两独立,我们也称其共同(mutal)独立 - 当然,在真实世界中变量太多,往往不能保证独立性,但是其他变量的干扰往往是间接的(mediated)而非直接的,因而我们可以使用条件概率进行描述:如果
 ,则记
,则记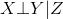
- 定理:如果存在函数g,h,使得对任意的x,y,z,p(z)>0,均有
 ,则
,则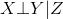
2.2.5连续随机变量
- 如果X是一个连续的随机变量,那么定义函数
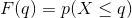 ,称为X的累积分布函数(cumulative distribution function,cdf),显然为一个单调递增函数。再定义
,称为X的累积分布函数(cumulative distribution function,cdf),显然为一个单调递增函数。再定义 ,称为概率密度函数(probability density function,pdf),则
,称为概率密度函数(probability density function,pdf),则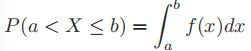
- 取间隔足够小,则
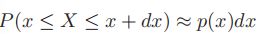
- 注意:在pdf中,p(x)可能会>1,因为它是F的导数,而只有F<1。而这里的p(x)并不是发生x的概率,因为x根本不是一个事件,发生的概率为0,这里的p(x)是在x附近的事件发生的密度。
- 笔者补充:事实上,一般的离散随机变量,通过定义定义域外的点处概率为0,可以延拓为连续随机变量。例如,在抛硬币的时候,p(X=0)=p(X=1)=1/2,则定义其余p(X=k)=0,我们得到了其cdf:
 ,当然了,因为存在断点,其导函数(pdf)不存在。
,当然了,因为存在断点,其导函数(pdf)不存在。
2.2.6分位数(quantiles)
- 由于F单调递增,我们可以定义F的反函数
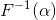 ,称为
,称为 对
对 的分位数。例如,
的分位数。例如, 即为X的分布的中位数‘;而
即为X的分布的中位数‘;而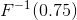 和
和 分别称为上下四分位数(quartiles)
分别称为上下四分位数(quartiles)
2.2.7均值与方差(mean and variance)
2.3一些常见的离散分布(discrete distributions)
在这一部分,我们会回顾一些常见的定义在离散状态空间上的分布
2.3.1二项分布和伯努利分布(binomial&Bernoulli distribution)
2.3.2多项分布和多项伯努利分布(multinomial)
2.3.3泊松分布(Poisson distribution)
2.3.4经验分布(emperical distribution)
2.4一些常见的连续分布
2.4.1高斯分布(Gaussian distribution)
- 高斯分布:

- 我们经常讨论高斯分布的精确度(precision),这里我们使用
 来表示,精确度越大则分布曲线越窄。
来表示,精确度越大则分布曲线越窄。 - 高斯函数的cdf:
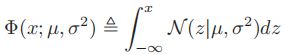
- 这个积分并没有闭合形式表达式(closed form expression,即使用有限次初等运算得到的表达式),不过,我们可以用误差函数(error function, erf)对它进行估计:
 ,其中
,其中 ,
,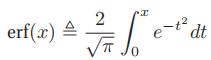
- 高斯分布是在统计中使用最为广泛的分布。一方面,它的两个变量都很容易进行解释,一个是方差,一个是均值;另一方面,中心极限定理(central limit theorem)告诉我们相互独立的随机变量的加和接近高斯分布,因此它在过滤噪声方面的效果非常优良;最后,高斯分布做出的预测的假设是最少的(可以操作的空间最大);最后,它的数学形式很简洁,让结果易于进行调整。
2.4.2退化概率密度函数(degenerate pdf)
- 在高斯分布中,我们假设方差趋近于0,则其会变成一个类似“尖钉”的形状,中心为
 ,可以表示为
,可以表示为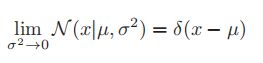 ,称为狄拉克delta函数,其中
,称为狄拉克delta函数,其中 为狄拉克函数(在自变量取0时值为无穷,在其他的时候取值为0),并使得在实数域上的积分为1
为狄拉克函数(在自变量取0时值为无穷,在其他的时候取值为0),并使得在实数域上的积分为1 - delta函数的一个有用的性质就是它的筛性:
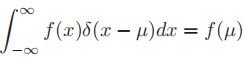
- 高斯分布的一个问题在于它对异常值比较敏感。这是因为它的log概率在远离中心点时以二次方速度衰减。因此,我们有一个鲁棒性更好的分布,即学生t分布(Student t distribution):
 ,其中
,其中 为均值,
为均值,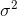 为尺度参数,
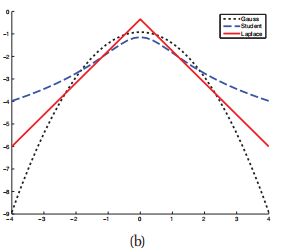
为尺度参数, 为自由度。如下图的log-concave所示,边际点对高斯分布的影响显然更加明显(因为边际点很少,所以很小的边际波动就可以引发很大的扰动;而蓝色的student分布则明显好得多)
为自由度。如下图的log-concave所示,边际点对高斯分布的影响显然更加明显(因为边际点很少,所以很小的边际波动就可以引发很大的扰动;而蓝色的student分布则明显好得多)
- 为了保证方差有限,我们需要自由度
 ,因而常用
,因而常用 ,而当
,而当 时,student分布会向高斯分布收敛
时,student分布会向高斯分布收敛
2.4.3拉普拉斯分布(Laplace distribution)
另一个尾巴比较重(heavy tail,即异常值影响小)的分布是拉普拉斯分布,也被称为双边指数分布(double sided exponential distribution)。
![]() ,其中
,其中![]() 为位置参数,
为位置参数,![]() 为规模参数
为规模参数
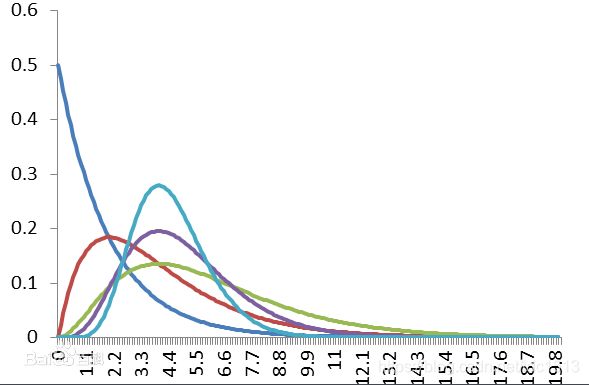
2.4.4伽马分布(gamma distribution)
一些特例分布:
2.4.5beta分布
![]()
2.4.6帕累托分布(Pareto distribution)
![]()
2.5联合概率分布
之前,我们一直着眼于单变量的概率分布。接下来我们将会讨论一个更具挑战性的问题:多个相关变量的分布;这也将会是本书的核心。
2.5.1协方差和相关系数(covariance&correlation)
- 协方差描述两个一维变量XY之间的线性相关程度,定义为:

- 如果x是d维的随机向量,记
 ,那么x的协方差矩阵定义为
,那么x的协方差矩阵定义为
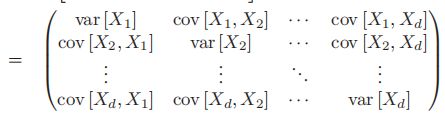 ,其中
,其中![var[X]=cov[X,X]](http://img.e-com-net.com/image/info8/917fb22b3e43411da0e4d8b66cf825e7.gif) ,为随机变量X的方差(variance)
,为随机变量X的方差(variance) - 注意这是一个半正定矩阵,证明可以看https://zhidao.baidu.com/question/920597155846911579.html,核心思路为:
![y^Tcov[x]y=y^TE[(x-\mu)(x-\mu)^T]y=E[y^T(x-\mu)(x-\mu)^Ty]\ \ \ \ \ \ \\ \ \ =E[((x-\mu)^Ty)^T((x-\mu)^Ty)]](http://img.e-com-net.com/image/info8/dc0e941e984643c6a30d13f74e8e42d4.gif)
- 协方差的取值可以为0到正无穷。有的时候我们希望使用一个有界的数值,因此会使用皮尔森(Pearson)的相关系数(correlation coefficient)
- X和Y两个一维随机变量的相关系数定义为:
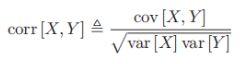
- 之后同样的定义d维变量x的相关矩阵:
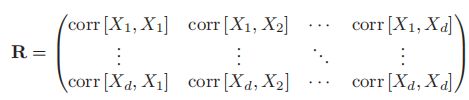
- 容易发现,R中每一个corr[X,Y]的取值范围均在±1之间,且对角线全为1
- (证明使用cauchy不等式可秒,并且可得出取±1条件即为X,Y正/负相关)
- 如果X和Y无关,那么p(X,Y)=p(X)P(y),因此cov[X,Y]=corr[X,Y]=0
- 但是,corr[X,Y]=0不一定推出X,Y无关,如
 ,则
,则![corr[X,Y]=E(XY)-E(X)E(Y)=E(X^3)-0=0](http://img.e-com-net.com/image/info8/120ccc0ade914aaaa349445d3e79f2eb.gif) ,这实际上是因为协方差描述的是X,Y之间的线性相关程度,并不是一切相关程度
,这实际上是因为协方差描述的是X,Y之间的线性相关程度,并不是一切相关程度
2.5.2多元高斯分布(multivariate Gaussian)
- 多元高斯分布,或者多元正态分布(multivariate normal,MVN),是最为常用的连续变量的联合概率密度函数。
- MVN的pdf的定义为:
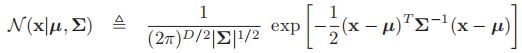
- 其中
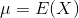 为D维均值向量,
为D维均值向量,![\Sigma=cov[x]](http://img.e-com-net.com/image/info8/f730efbead8e47a280f25de9df4b124e.gif) 为D阶协方差矩阵,有的时候我们会称其为精度矩阵(precision matrix)或浓缩矩阵(concentration matrix),
为D阶协方差矩阵,有的时候我们会称其为精度矩阵(precision matrix)或浓缩矩阵(concentration matrix),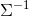 为协方差矩阵的逆矩阵,而前面的系数保证该分布的积分为1
为协方差矩阵的逆矩阵,而前面的系数保证该分布的积分为1 - 关于多元高斯分布公式的来龙去脉,https://zhuanlan.zhihu.com/p/58987388解释的非常清楚,同时使用变量替换(Jacobi)给出了积分为1的证明。事实上,这就是协方差矩阵的本质之一:假设变换
 使得
使得 的各个变量变为相互无关,则‘:
的各个变量变为相互无关,则‘:![cov[x]=E[(x-\mu)(x-\mu)^T]=E[(Bz)(Bz)^T]=Bcov[z,z]B^T=BB^T](http://img.e-com-net.com/image/info8/959ab0e92bcf468480315d0fd45aac8a.gif) ,其中最后一步用到了z的无关性,同时我们便有
,其中最后一步用到了z的无关性,同时我们便有
- 显然,不同的协方差矩阵定义了不同形状的多元正态分布,其中,满协方差矩阵有D(D+1)/2个参数,对角协方差矩阵有D个参数,球形(spherical)或各向同(isotropic)协方差矩阵有1个参数(
 )
)
2.5.3多元学生t分布
- 与一元的情形相同,多元学生t分布的鲁棒性比多元正态分布更强,其pdf为:
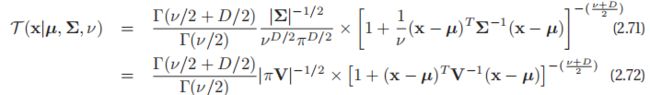
- 其中
 称为尺度矩阵(scale matrix),因为它不完全是协方差矩阵;
称为尺度矩阵(scale matrix),因为它不完全是协方差矩阵;
- 它的长尾性(即不受异常值影响的性质)比正态要好,而且
 越小就越好
越小就越好
2.5.4狄利克雷分布
2.6随机变量的变量替换(transformation)
如果随机变量![]() ,且
,且![]() ,那么y的分布是怎么样的呢?这是本节将要解答的问题。
,那么y的分布是怎么样的呢?这是本节将要解答的问题。
2.6.1线性变换
- 如果f是一个线性函数,即
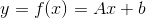 ,则我们很容易算出y的方差和均值:
,则我们很容易算出y的方差和均值: - 根据期望的线性性质(linearity of expectation),我们知道
![E[y]=E[Ax+b]=A\mu+b](http://img.e-com-net.com/image/info8/f69c6e37b39c4253b6b3cbf3a04ab94f.gif)
- 对于方差,我们则有:
![cov[y]=cov[Ax+b]=A \Sigma A^T](http://img.e-com-net.com/image/info8/e6d774e29a3f4cad9f523cea9808354b.gif) ,证明使用直接分解法即可
,证明使用直接分解法即可 - 当然了,只有高斯分布才被方差和均值完全确定,因此我们最好想个办法把y的整个分布求出来
2.6.2一般变换
- 如果X是一个离散变量,则

- 如果X是一个连续变量,则我们不能使用上面的等式,因为在pdf中p为密度,在单点处取值无意义,因此,我们使用cdf进行计算:
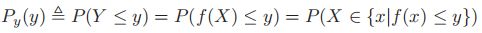 ,之后我们再通过求导即可计算出y的pdf
,之后我们再通过求导即可计算出y的pdf- 若P为单调递增函数,则反函数存在,从而有
 ,求导即得
,求导即得 ,其中
,其中
- 同时,由于pdf的非负性,我们两边取abs得到一个一般的表达式:
 ,这个公式被称为变量替换公式(change of variables formula),我们也可以用一下的方式更好地理解它:如果将
,这个公式被称为变量替换公式(change of variables formula),我们也可以用一下的方式更好地理解它:如果将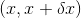 内的概率变为
内的概率变为 ,则有
,则有
2.6.2.1多元变量替换
2.6.3中心极限定理(central limit theorem)
- 现在假设有N个随机变量,其pdf分别为
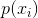 ,每一个的均值和方差都是
,每一个的均值和方差都是 和
和 .我们假设每一个变量都是独立同分布的(independent and identically distributed,iid),亦即在重复试验之间变量两两独立且分布函数相同。
.我们假设每一个变量都是独立同分布的(independent and identically distributed,iid),亦即在重复试验之间变量两两独立且分布函数相同。 - https://zhuanlan.zhihu.com/p/52530189对iid进行了比较详细的解释,事实上iid本质上就是假设所有的样本都是由相同的随机分布产生的,只有这样才能明确机器学习的目标。(如果每一个样本的产生函数都不相同,那么要怎么才能学习这个函数?!)
- 令
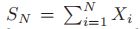 为所有随机变量的和,我们可以证明:随着N的增大,
为所有随机变量的和,我们可以证明:随着N的增大,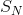 的分布趋近于正态分布:
的分布趋近于正态分布:
- 也就是说,
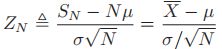 的分布收敛于标准正态分布
的分布收敛于标准正态分布 - 注:如果
 ,则
,则 符合标准正态分布
符合标准正态分布 - 笔者注:那么,中心极限定理到底说了个什么东西呢?很简单,假如我们取一个[0,1]上随机分布(不一定均匀)的随机数N次,显然每次取数都是独立且相互同分布的,那么,根据中心极限定理,当N趋近于无穷的时候,这么多次取随机数的均值符合正态分布。但是,这个定理的诠释内容其实更加广泛。举个例子,假如我们随机地拍摄照片,每张照片上都有随机数量的鸟。我们假设鸟的数量的分布是独立同分布的,那么如果我们拍摄N次照片,把这些照片上的鸟的数量取平均值。即使我们不知道这些鸟的分布是什么,我们仍然可以知道这个平均值的分布一定符合正态分布。这就是中心极限定理的威力所在。
- 至于中心极限定理的证明,书上没有直接给出,但是https://zhuanlan.zhihu.com/p/85233692给出的证明非常简洁,可供参考。
- 图示为笔者对U(0,pi/2)做y=sin(x)的变换后进行30次求和后做10000次重复试验得到的分布,可以看出,非常符合正态分布。源码贴在这里:https://mp.csdn.net/console/editor/html/107770694
2.7蒙特卡洛近似(Monte Carlo Approximation)
- 通常情况下,给定
 和
和 ,使用变量替换公式计算随机变量
,使用变量替换公式计算随机变量 的分布函数是十分困难的。
的分布函数是十分困难的。 - 这时,蒙特卡洛近似是一个简单高效的替代。
- 在蒙特卡洛近似中,我们将会使用S个样例的分布来估计
 的变量分布:
的变量分布: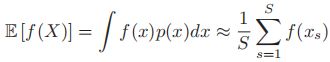 ,其中
,其中
- 由于f的任意性,蒙特卡洛方法的应用非常广泛,例如:
- 取
 ,得到
,得到
- 取
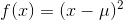 ,得到
,得到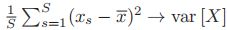
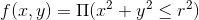
- 取
 ,得到
,得到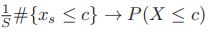
2.7.1举例:变量替换中的蒙特卡洛方法
- 假如
 ,且
,且 ,我们可以通过随机取样后求平方来计算
,我们可以通过随机取样后求平方来计算 的经验分布
的经验分布
2.7.2举例:用蒙特卡洛方法计算π值
- 半径为r的圆的面积为
 ,我们要求
,我们要求
- 令
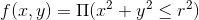 为指示函数,p(x),p(y)为[-r,r]上的均匀分布,则p(x)=p(y)=1/(2r),则:
为指示函数,p(x),p(y)为[-r,r]上的均匀分布,则p(x)=p(y)=1/(2r),则: 
- 笔者注:为什么要取p(x),p(y)为[-r,r]上的均匀分布呢?其实并不是必须的。事实上,蒙特卡洛方法对p并没有什么要求,即使我们取x,y为μ=-100r的正态分布,也是可以成立的。但是,这样的话,均匀取样会是一个大问题,而增加系数把I转化为蒙特卡洛的形式也是另一个问题,所以,我们一般使用均匀分布。同样的,[-r,r]的选取也不是必须的。我们完全可以选择x,y为[-2r,5r]上的均匀分布,容易看出这不会影响我们得到的结果。但是,另一方面,我们不能选取[-r/2,r/2],否则算出来的将会是正方形的面积。这则是因为在蒙特卡洛方法中我们对f(x,y)p(x)p(y)的积分的定义域事实上要求是
![[-\infty, \infty]](http://img.e-com-net.com/image/info8/6723b99c9f35405c8befb79664963781.gif) ,只是本例中特征函数f(x,y)在[-r,r]²外一定取0,因此外面的部分略去不算罢了。
,只是本例中特征函数f(x,y)在[-r,r]²外一定取0,因此外面的部分略去不算罢了。
2.7.3蒙特卡洛近似的精度(Accuracy)
- 蒙特卡洛近似的精度随着样本数量的增大而增大。
- 如果我们假设样本数量为S,函数方差
![\sigma^2=var[f(X)]=E[f(X)^2]-E[f(X)]^2](http://img.e-com-net.com/image/info8/d87164113a70457e90a1da86b9129c78.gif) 实际均值为
实际均值为![\mu=E[f(X)]](http://img.e-com-net.com/image/info8/0bb3f7f0445f46e5968092531c94427a.gif) ,并且蒙特卡洛估计的均值为
,并且蒙特卡洛估计的均值为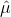 ,则我们可以证明
,则我们可以证明 (这是中心极限定理的推论)
(这是中心极限定理的推论) - 当然,虽然
 是未知的,但是我们也可以使用MC(Monte Carlo)对其进行估计:
是未知的,但是我们也可以使用MC(Monte Carlo)对其进行估计:
- 于是,我们有
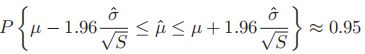 ,其中
,其中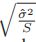 被称为标准误差(standard error),用以估计
被称为标准误差(standard error),用以估计 的不确定程度
的不确定程度 - 因此,当我们希望在95%的数据上得到的精度在±ε之间时,我们应该令
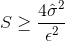
2.8信息论
- 信息论的目标是对数据进行压缩修饰(compact fashion),即数据压缩(data compression)或者信息编码(source coding);但是同时在传输和存储信息的时候,又要求容错率高(robust to errors),即误差修正(error correction)或者信道编码(channel coding)。也就是说,即要求信息尽可能压缩,又要求保真度高。
- 这个任务看起来跟机器学习和概率论简直是风马牛不相及,但是它们其实有着密切的联系。在信息论中,我们的目标是把最短的密文分配给最常见的数据,而把较长的密文分配给不常见的数据。这一点与自然语言的情况完全相同—"a""the""and"是最为常用的单词,因此也最短。*另一方面,当我们将信息在噪声信道中传递时,我们希望建立一个良好的模型,以预测对方到底想要传达什么信息。这两种要求都需要我们建立一个可以预测数据类型的模型,而这正是机器学习的核心问题之一。
- *笔者注:事实上汉语则不太是这样,这是因为英语等拼音文字的字母数量非常有限,事实上更加接近计算机中密文—明文的一一对应方式;而汉语等象形文字则基本上都是单字,一方面文字的结构和笔画有着特定的含义,不太容易更改;另一方面文字的笔画对书写时间的影响较小(在英语中长度为10个字母的单词的书写时间是1个字母的10倍,但是汉语因为单字的大小相同,10笔的汉字的书写时间至多是1笔的汉字的3倍,如果是拼音输入的话影响就更加有限了)
- 当然,我们不会介绍太多关于信息论的内容,只会介绍一些我们将要用到的基本概念。
2.8.1熵(entropy)
- 一个分布为p的随机变量X的熵定义为
 ,用以描述它的不确定性。
,用以描述它的不确定性。 - 特别的,一个存在K种状态的随机变量X的熵定义为:
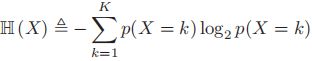
- 一般我们使用以2为底的对数,此时单位元称为比特(bits,binary digits);如果我们使用以e为底的对数,那么单位元则称为nat. 例如,如果X∈[1,2,3,4,5]的分布为p=[0.25,0.25,0.2,0.15,0.15],则H=2.2855.
- 在离散变量中,熵值最大的是均匀分布。例如,若一个离散变量有K个取值,则其熵值的最大值在P(x=i, all i)=1/K时取得,值为
 ;而其熵值的最小值为0,在某一状态处值为1,其余为0时取得(在连续取值时则用狄拉克delta函数取得),这样的分布不存在任何不确定性,称为确定分布(determintstic distribution)。
;而其熵值的最小值为0,在某一状态处值为1,其余为0时取得(在连续取值时则用狄拉克delta函数取得),这样的分布不存在任何不确定性,称为确定分布(determintstic distribution)。
2.8.2KL散度(KL divergence)
- 通过KL散度(Kullback-Leibler divergence,又称相对熵relative entropy),我们可以估计两个概率分布p和q的不相似程度。
- KL散度定义如下:
 (如果连续,则求和变为pdf的积分),也可以记为
(如果连续,则求和变为pdf的积分),也可以记为
- 其中
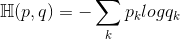 称为p,q的交叉熵(cross entropy)
称为p,q的交叉熵(cross entropy) - 注1:以上的
 在离散时均是对p的定义域求和。q的定义域不一定需要与p的相同
在离散时均是对p的定义域求和。q的定义域不一定需要与p的相同 - 注2:KL散度恒大于0,但是具有不对称性(KL(P||Q)≠KL(Q||P)),因此不是距离的度量。如果需要具有对称性的表达,需要使用JS散度(Jensen-Shannon divergence),定义为

- 交叉熵的实际含义为:分布为p的数据使用模型q进行编码时的平均比特数。而一般的熵
 则表示了使用真实模型模拟的时候我们所需要的比特数。因此,交叉熵的含义即为这两者之间的差值,也就是我们在编码数据时需要的额外的比特数。
则表示了使用真实模型模拟的时候我们所需要的比特数。因此,交叉熵的含义即为这两者之间的差值,也就是我们在编码数据时需要的额外的比特数。 - 下面我们证明KL散度恒≥0,取等当且仅当p=q:
- 使用琴生不等式(Jensen`s inequality),结合
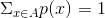 ,我们有:
,我们有: 
- 根据琴生不等式的取等条件:
 和最后一步放缩的取等条件:p(x)的定义域与q(x)完全相同,结合和1性,显见p(x)=q(x)
和最后一步放缩的取等条件:p(x)的定义域与q(x)完全相同,结合和1性,显见p(x)=q(x) - 这个定理的一个重要推论就是均匀分布的熵最大性:对任意的p(x),代入q(x)为均匀分布,即可得到
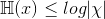 的结论
的结论 - 这也是拉普拉斯的不充分推理原则(principle of insufficient reason)的表达方式之一:也就是说,当我们对分布的优劣没有什么直观感觉时,我们的先验分布应该取均匀分布。
2.8.3互信息(mutual information)
- 考虑两个随机变量X和Y,现在我们希望知道其中一个变量告诉了我们多少关于另一个变量的信息。我们可以使用相关系数来度量这种关系,即
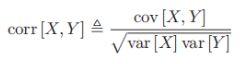 . 但是,根据我们之前的分析,相关系数度量的主要是两个变量之间的线性关系,即使是Y=X²这样紧密的关系也会被度量为不相关。
. 但是,根据我们之前的分析,相关系数度量的主要是两个变量之间的线性关系,即使是Y=X²这样紧密的关系也会被度量为不相关。 - 为此,我们引入互信息(mutual information, MI)的概念:
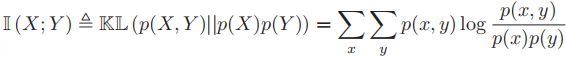 (p(X,Y):X,Y的联合概率,即同时发生X和Y的概率);容易证明(真的只要展开一下),MI也可以写成下面的等价形式:
(p(X,Y):X,Y的联合概率,即同时发生X和Y的概率);容易证明(真的只要展开一下),MI也可以写成下面的等价形式: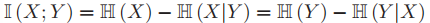 ,其中
,其中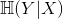 为条件熵,定义为
为条件熵,定义为
- 变换后,我们就可以解释为什么互信息能够描述X和Y之间的相关性——它代表了X的不确定性和在观测到Y后X的不确定性的差值。
- 注:互信息确实是描述X,Y关系的极好工具——在相关系数中,我们只使用E[XY]-E[X]E[Y]来度量X,Y之间的差值。但是这样丢失了非常多的信息;而在互信息中,我们使用XY和X,Y的全空间分布的KL散度来度量X,Y的相关性,自然容纳了非常多的信息。
- 与MI紧密相关的一个数据为逐点互信息(pointwise mutual information, PMI)对于两个事件(不是随机变量)x,y,其PMI定义为:
 ,这度量了x,y同时发生与分别发生的概率的差异
,这度量了x,y同时发生与分别发生的概率的差异
2.8.3.1连续随机变量的互信息
- 上面的关于MI的公式是为离散随机变量定义的。对于连续随机变量来说,最好的处理方式是将它们离散化(discretize/ quantize),将每一个连续变量的取值范围分割成小的区间,然后计算这些区间上的频数分布(histogram)后转化为离散形式进行处理。
- 不幸的是,区间的数量、区间界限的选取,都可能会对结果造成非常显著的影响。因此,除了一开始就用密度估计以外,另一种方式是常数很多种不同的区间大小和位置,然后计算出获得的MI中的最大值。这种标准的统计方法称为最大信息系数法(maximal information coefficient),用数学公式来写就是:
 ,其中
,其中 ,若我们将区间划分为x个×y个,且B为给定的xy的上界(不可能取得无限大),使用动态规划的方法很容易运算出这个最值问题。
,若我们将区间划分为x个×y个,且B为给定的xy的上界(不可能取得无限大),使用动态规划的方法很容易运算出这个最值问题。- 这里的解释稍微有些贫瘠,因此可以观看https://www.omegaxyz.com/2018/01/18/mic/,通过一些例子学习如何计算MIC
- 笔者注:MIC的优点在于既能挖掘线性关系,又能挖掘非线性关系,和相关系数混合使用效果更佳。其本质我认为在于发掘x和y之间是否存在一一对应的关系。