DBSCAN算法详解

原文地址：http://blog.csdn.net/star_dragon/article/details/50728972

DBSCAN算法详解与实现

  DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法是一种基于空间密度的聚类算法，不同于其他传统聚类，其将空间密度较高的区域聚为一簇，生成的簇没有固定形状（与之相比kmeans聚类形状为圆，em聚类形状为椭圆）,没有偏倚。DBSCAN算法除了可以实现聚类效果，也可以用于寻找数据中的噪声，这是传统聚类算法做不到的，以下介绍相关概念。

---

• 算法参数

  dbscan算法是一种基于密度聚类的算法，对于密度的一种直观的理解则是在某单位范围内含有多少东西，而在本算法中则定义了两个参数 r 与 minPts。对于任一数据点，在其 r 邻域内所包含的数据点的数量（包括其自身）就是密度，而 minPts 则是一个算法中使用到的阈值。

• 核心概念

  核心点：若某个点的密度达到算法设定的阈值（即 r 邻域内点的数量不小于 minPts），则其为核心点。 
  直接密度可达：若某点p在点q的 r 邻域内，且q是核心点，则称p从q出发直接密度可达。 
  密度可达：若有一个点的序列q₀、q₁、…q_k，对任意q_i从q_i-1出发是直接密度可达的，则称从q₀到q_k密度可达，这实际上是直接密度可达的“传播”。 
  密度相连：若从某核心点p出发，点q和点k都是密度可达的，则称点q和点k是密度相连的。

  以上几个概念可以从下图（图片来自维基百科）直观的看出，圆圈代表 r 邻域，红色点为核心点，从点A出发，B、C均是密度可达的，B、C则是密度相连的，且B、C为边界点，而N为噪声点（边界点、噪声点的概念在算法部分详述）。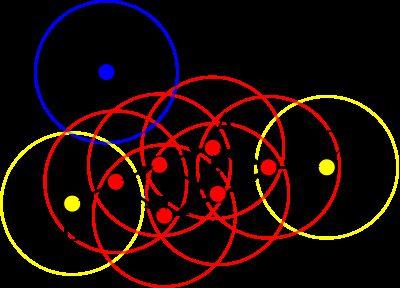 

• 算法思想

  dbscan算法本质上是一个寻找类簇并不断扩展类簇的过程，要形成类簇首先数据密度要满足要求。对任意点p，若其是核心点，则以p为中心 r 为半径可以形成一个类簇C，扩展类簇的方法则是遍历簇中的点，若有点q是核心点，则将q的 r 邻域内的点也划入类C，递归执行直到C不能再扩展。 
  以上图为例，假设 minPts 为3，r 为图中圆圈的半径，算法从A开始，经计算其为核心点，则将点A及其邻域内的所有点（共4个）归为类Q，接着尝试扩展类Q。查询可知类Q内所有的点均为核心点（红点），故皆具有扩展能力，点C也被划入类Q。在递归拓展的过程中，查询得知C不是核心点，类Q不能从点C处扩充，称C为边界点。边界点被定义为属于某一个类的非核心点。在若干次扩展以后类Q不能再扩张，此时形成的类为图中除N外的所有的点，点N则成为噪声点，即不属于任何一个类簇的点，等价的可以定义为从任何一个核心点出发都是密度不可达的。在上图中数据点只能聚成一个类，在实际使用中往往会有多个类，即在某一类扩展完成后另外选择一个未被归类的核心点形成一个新的类簇并扩展，算法结束的标志是所有的点都已被划入某一类或噪声，且所有的类都不可再扩展。 
  算法伪代码如下，摘自维基百科：

DBSCAN(D, eps, MinPts) {//此处eps即为半径r
   C = 0
   for each point P in dataset D {//遍历数据集
      if P is visited
         continue next point
      mark P as visited
      NeighborPts = regionQuery(P, eps)//查询p的邻域内的所有点
      if sizeof(NeighborPts) < MinPts
         mark P as NOISE//非核心点标记为噪声，注意这并非最终结果，可能在后面被归入某一类成为边界点
      else {
         C = next cluster
         expandCluster(P, NeighborPts, C, eps, MinPts)//若是核心点，则扩展该类
      }
   }
}

expandCluster(P, NeighborPts, C, eps, MinPts) {
   add P to cluster C
   for each point P' in NeighborPts {//遍历邻域内所有点，查询其是否可以拓展类 
      if P' is not visited {
         mark P' as visited
         NeighborPts' = regionQuery(P', eps)
         if sizeof(NeighborPts') >= MinPts//若是核心点，则其邻域内的点也要继续遍历
            NeighborPts = NeighborPts joined with NeighborPts'
      }
      if P' is not yet member of any cluster//对邻域内的所有点，若尚未归类，则将其划入类C
         add P' to cluster C
   }
}

regionQuery(P, eps)
   return all points within P's eps-neighborhood (including P)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

• 算法分析 
  1.主循环中从哪个点开始遍历并未定义，之所以强调这一点是不同的起始点可能导致不同的聚类结果。 
  2.当某一边界点既可以划入类簇1，也可以划入类簇2，那么其最终所处类簇与遍历时的顺序有关，这也是上面第一条的原因。 
  3.时间复杂度上，对每个点都要求其邻域内的所有点，复杂度为O(n²)，但在低维空间下若采用kd树、r树等数据结构则可降低至O(nlogn)。在扩展函数中需要合并两个集合，复杂度为O(mn)，m、n分别为两个集合的大小。同时注意到在扩展函数中由于对每个核心点都要进行集合合并操作，算法的绝大部分时间都将耗费在拓展函数上，算法完成时间也高度依赖于两个算法参数，尤其是 r 。

• 算法实现

  自开始学习dbscan，本人前前后后共实现了多个版本的算法，从最开始的没有任何优化的dbscan，到后面加入kd树、r树等数据结构的版本，再到往后为了兼容weka而在weka源码上修改而来的各种版本，前后版本有6、7个之多，在此就不再一一列出，下面给出一个kd树实现的版本。

private void cluster(List list){ 
    dataSource = copyList(list);//简单的复制数据，并非必要
    init(dataSource);//重新组织数据，使用kd树存储以加速近邻查询，可用r树等代替
    initNeibors();//计算出每个点的r邻域内的所有点并存储，注意这将耗费额外的存储空间，斟酌使用
    for(Point p : dataSource){                     //遍历数据集
        if(p.getCls() == -1){                      //如果未分配簇号
            List neibors = p.getNeibros();  //求出r邻域点集
            if(neibors.size() < minPts){           //如果不是核心点
                continue;
            }
            expandCluster(p, neibors, cls++);      //拓展该簇
        }
    }
}

private void expandCluster(Point p, List neibors, int cls){
    int size = neibors.size();
    for(int i = 0; i < size; i++){
        Point neibor = neibors.get(i);
        if(neibor.getCls() == -1){          //如果未分配簇号则把核心点簇号分配给它
            neibor.setCls(cls);
        } else {
            continue;
        }
        List neiList = neibor.getNeibros();    
        if(neiList.size() < minPts){
            continue;
        }
        for(Point pp : neiList){           //如果其是核心点，则将其r邻域点集也加入待拓展序列
            if(!list.contains(object2) &&(seed.getCls() == DataObject.NOISE ||
                    seed.getCls() == DataObject.NOTVISITED)){//只考虑未被分类的点
                list.add(object2);
                size++;
            }
        }
    }
}

//初始化每个点的r邻域
private void initNeibors(){
    for(Point p : dataSource){
        List neibors = new ArrayList();
            scanNeibor(p, tree, neibors);//此处的tree即是由全部数据组织成的kd树
        p.setNeibros(neibors);
    }
}

//递归查找p的r邻域，root初始化为树根，可简单替换为穷举搜索
private void scanNeibor(Point p, Point root, List neibors){
    if(root == null){
        return;
    }
    if(getDest(p, root) <= r){
        neibors.add(root);//当前结点与p的距离若小于阈值
    }
    if(root.getType() == KDNode.LEAVE){
        return;//叶子节点则返回
    }
    int axis = root.getAxis();//当前结点的分割平面，详见kd树相关内容
    double[] attr1 = p.getAttr();
    double[] attr2 = root.getAttr();        
    if(attr1[axis] <= attr2[axis]){//若p点位于当前分割平面的左边，则将当前结点的左空间也纳入搜索范围
        scanNeibor(p, (Point)root.getLeft(), neibors);
        if(Math.abs((attr1[axis] - attr2[axis])) <= r){
            //若p点的r邻域与分割平面的交集不为空，那么分割平面的两侧都要搜索
            scanNeibor(p, (Point)root.getRight(), neibors);
        }
    } else {//位于分割平面的右边
        scanNeibor(p, (Point)root.getRight(), neibors);
        if(Math.abs((attr1[axis] - attr2[axis])) <= r){
            //p点的r邻域与分割平面的交集不为空
            scanNeibor(p, (Point)root.getLeft(), neibors);
        }
    }
}