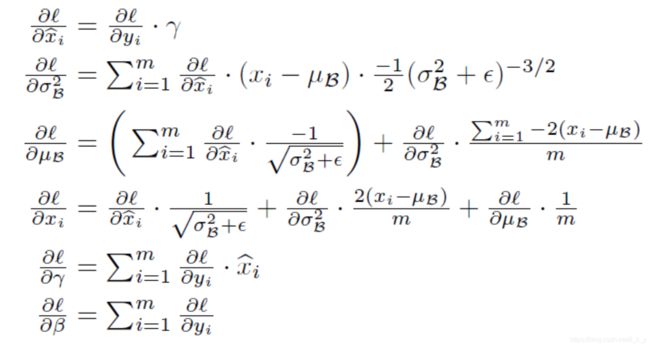cs231n assignment2 Batch Normalization
Batch normalization 优点:
- 减少坏初始化的影响
- 加快模型的收敛速度
- 可以用大些的学习率
- 能有效地防止过拟合
Batch normalization: forward
import time
import numpy as np
import matplotlib.pyplot as plt
from cs231n_2.classifiers.fc_net import *
from cs231n_2.data_utils import get_CIFAR10_data
from cs231n.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs231n.solver import Solver
def rel_error(x, y):
""" returns relative error """
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
def print_mean_std(x,axis=0):
print(' means: ', x.mean(axis=axis))
print(' stds: ', x.std(axis=axis))
print()
# Batch normalization: forward
# Check the training-time forward pass by checking means and variances
# of features both before and after batch normalization
#
# Simulate the forward pass for a two-layer network
np.random.seed(231)
N, D1, D2, D3 = 200, 50, 60, 3
X = np.random.randn(N, D1)
W1 = np.random.randn(D1, D2)
W2 = np.random.randn(D2, D3)
a = np.maximum(0, X.dot(W1)).dot(W2)
print('Before batch normalization:')
print_mean_std(a,axis=0)
gamma = np.ones((D3,))
beta = np.zeros((D3,))
# Means should be close to zero and stds close to one
print('After batch normalization (gamma=1, beta=0)')
a_norm, _ = batchnorm_forward(a, gamma, beta, {'mode': 'train'})
print_mean_std(a_norm,axis=0)
gamma = np.asarray([1.0, 2.0, 3.0])
beta = np.asarray([11.0, 12.0, 13.0])
# Now means should be close to beta and stds close to gamma
print('After batch normalization (gamma=', gamma, ', beta=', beta, ')')
a_norm, _ = batchnorm_forward(a, gamma, beta, {'mode': 'train'})
print_mean_std(a_norm,axis=0)# Check the test-time forward pass by running the training-time
# forward pass many times to warm up the running averages, and then
# checking the means and variances of activations after a test-time
# forward pass.
np.random.seed(231)
N, D1, D2, D3 = 200, 50, 60, 3
W1 = np.random.randn(D1, D2)
W2 = np.random.randn(D2, D3)
bn_param = {'mode': 'train'}
gamma = np.ones(D3)
beta = np.zeros(D3)
for t in range(50):
X = np.random.randn(N, D1)
a = np.maximum(0, X.dot(W1)).dot(W2)
batchnorm_forward(a, gamma, beta, bn_param)
bn_param['mode'] = 'test'
X = np.random.randn(N, D1)
a = np.maximum(0, X.dot(W1)).dot(W2)
a_norm, _ = batchnorm_forward(a, gamma, beta, bn_param)
# Means should be close to zero and stds close to one, but will be
# noisier than training-time forward passes.
print('After batch normalization (test-time):')
print_mean_std(a_norm,axis=0)batchnorm_forward 实现:
def batchnorm_forward(x, gamma, beta, bn_param):
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# #
# You should store the output in the variable out. Any intermediates #
# that you need for the backward pass should be stored in the cache #
# variable. #
# #
# You should also use your computed sample mean and variance together #
# with the momentum variable to update the running mean and running #
# variance, storing your result in the running_mean and running_var #
# variables. #
# #
# Note that though you should be keeping track of the running #
# variance, you should normalize the data based on the standard #
# deviation (square root of variance) instead! #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
#######################################################################
sample_mean = np.mean(x, axis=0)
sample_var = np.var(x, axis=0)
x_hat = (x - sample_mean) / (np.sqrt(sample_var + eps))
out = gamma * x_hat + beta
cache = (x, sample_mean, sample_var, x_hat, eps, gamma, beta)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
out = (x - running_mean) * gamma / (np.sqrt(running_var))
#######################################################################
# END OF YOUR CODE #
#######################################################################
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
Batch normalization: backward
# Batch normalization: backward
# Gradient check batchnorm backward pass
np.random.seed(231)
N, D = 4, 5
x = 5 * np.random.randn(N, D) + 12
gamma = np.random.randn(D)
beta = np.random.randn(D)
dout = np.random.randn(N, D)
bn_param = {'mode': 'train'}
fx = lambda x: batchnorm_forward(x, gamma, beta, bn_param)[0]
fg = lambda a: batchnorm_forward(x, a, beta, bn_param)[0]
fb = lambda b: batchnorm_forward(x, gamma, b, bn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma.copy(), dout)
db_num = eval_numerical_gradient_array(fb, beta.copy(), dout)
_, cache = batchnorm_forward(x, gamma, beta, bn_param)
dx, dgamma, dbeta = batchnorm_backward(dout, cache)
#You should expect to see relative errors between 1e-13 and 1e-8
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))
batchnorm_backward 实现:
def batchnorm_backward(dout, cache):
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
###########################################################################
x, mean, var, x_hat, eps, gamma, beta = cache
N = x.shape[0]
dgamma = np.sum(dout * x_hat, axis=0)
dbeta = np.sum(dout * 1.0, axis=0)
dx_hat = dout * gamma
dx_hat_numerator = dx_hat / np.sqrt(var + eps)
dx_hat_denominator = np.sum(dx_hat * (x - mean), axis=0)
dx_1 = dx_hat_numerator
dvar = -0.5 * ((var + eps) ** (-1.5)) * dx_hat_denominator
dmean = -1.0 * np.sum(dx_hat_numerator, axis=0) + dvar * np.mean(-2.0 * (x - mean),axis=0)
dx_var = dvar * 2.0 / N * (x - mean)
dx_mean = dmean * 1.0 / N
dx = dx_1 + dx_var + dx_mean
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
Fully Connected Nets with Batch Normalization
np.random.seed(231)
N, D, H1, H2, C = 2, 15, 20, 30, 10
X = np.random.randn(N, D)
y = np.random.randint(C, size=(N,))
# You should expect losses between 1e-4~1e-10 for W,
# losses between 1e-08~1e-10 for b,
# and losses between 1e-08~1e-09 for beta and gammas.
for reg in [0, 3.14]:
print('Running check with reg = ', reg)
model = FullyConnectedNet([H1, H2], input_dim=D, num_classes=C,
reg=reg, weight_scale=5e-2, dtype=np.float64,
normalization='batchnorm')
loss, grads = model.loss(X, y)
print('Initial loss: ', loss)
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False, h=1e-5)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
if reg == 0: print()You should expect losses between 1e-4~1e-10 for W, losses between 1e-08~1e-10 for b, and losses between 1e-08~1e-09 for beta and gammas.
Batchnorm for deep networks
比较在DNN中是否使用 batch normalization 的区别
# Load the (preprocessed) CIFAR10 data.
data = get_CIFAR10_data()
for k, v in data.items():
print('%s: ' % k, v.shape)
# Batchnorm for deep networks
np.random.seed(231)
# Try training a very deep net with batchnorm
hidden_dims = [100, 100, 100, 100, 100]
num_train = 1000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
weight_scale = 2e-2
bn_model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization='batchnorm')
model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization=None)
bn_solver = Solver(bn_model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True,print_every=20)
bn_solver.train()
solver = Solver(model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=20)
solver.train()
def plot_training_history(title, label, baseline, bn_solvers, plot_fn, bl_marker='.', bn_marker='.', labels=None):
"""utility function for plotting training history"""
plt.title(title)
plt.xlabel(label)
bn_plots = [plot_fn(bn_solver) for bn_solver in bn_solvers]
bl_plot = plot_fn(baseline)
num_bn = len(bn_plots)
for i in range(num_bn):
label='with_norm'
if labels is not None:
label += str(labels[i])
plt.plot(bn_plots[i], bn_marker, label=label)
label='baseline'
if labels is not None:
label += str(labels[0])
plt.plot(bl_plot, bl_marker, label=label)
plt.legend(loc='lower center', ncol=num_bn+1)
plt.subplot(3, 1, 1)
plot_training_history('Training loss','Iteration', solver, [bn_solver], \
lambda x: x.loss_history, bl_marker='o', bn_marker='o')
plt.subplot(3, 1, 2)
plot_training_history('Training accuracy','Epoch', solver, [bn_solver], \
lambda x: x.train_acc_history, bl_marker='-o', bn_marker='-o')
plt.subplot(3, 1, 3)
plot_training_history('Validation accuracy','Epoch', solver, [bn_solver], \
lambda x: x.val_acc_history, bl_marker='-o', bn_marker='-o')
plt.gcf().set_size_inches(15, 15)
plt.show()
说明 Batch normalization 可以加快模型的收敛速度
Batch normalization and initialization
不同的初始化对BN的影响:
# Batch normalization and initialization
np.random.seed(231)
# Try training a very deep net with batchnorm
hidden_dims = [50, 50, 50, 50, 50, 50, 50]
num_train = 1000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
bn_solvers_ws = {}
solvers_ws = {}
weight_scales = np.logspace(-4, 0, num=20)
for i, weight_scale in enumerate(weight_scales):
print('Running weight scale %d / %d' % (i + 1, len(weight_scales)))
bn_model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization='batchnorm')
model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization=None)
bn_solver = Solver(bn_model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=False, print_every=200)
bn_solver.train()
bn_solvers_ws[weight_scale] = bn_solver
solver = Solver(model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=False, print_every=200)
solver.train()
solvers_ws[weight_scale] = solver
# Plot results of weight scale experiment
best_train_accs, bn_best_train_accs = [], []
best_val_accs, bn_best_val_accs = [], []
final_train_loss, bn_final_train_loss = [], []
for ws in weight_scales:
best_train_accs.append(max(solvers_ws[ws].train_acc_history))
bn_best_train_accs.append(max(bn_solvers_ws[ws].train_acc_history))
best_val_accs.append(max(solvers_ws[ws].val_acc_history))
bn_best_val_accs.append(max(bn_solvers_ws[ws].val_acc_history))
final_train_loss.append(np.mean(solvers_ws[ws].loss_history[-100:]))
bn_final_train_loss.append(np.mean(bn_solvers_ws[ws].loss_history[-100:]))
plt.subplot(3, 1, 1)
plt.title('Best val accuracy vs weight initialization scale')
plt.xlabel('Weight initialization scale')
plt.ylabel('Best val accuracy')
plt.semilogx(weight_scales, best_val_accs, '-o', label='baseline')
plt.semilogx(weight_scales, bn_best_val_accs, '-o', label='batchnorm')
plt.legend(ncol=2, loc='lower right')
plt.subplot(3, 1, 2)
plt.title('Best train accuracy vs weight initialization scale')
plt.xlabel('Weight initialization scale')
plt.ylabel('Best training accuracy')
plt.semilogx(weight_scales, best_train_accs, '-o', label='baseline')
plt.semilogx(weight_scales, bn_best_train_accs, '-o', label='batchnorm')
plt.legend()
plt.subplot(3, 1, 3)
plt.title('Final training loss vs weight initialization scale')
plt.xlabel('Weight initialization scale')
plt.ylabel('Final training loss')
plt.semilogx(weight_scales, final_train_loss, '-o', label='baseline')
plt.semilogx(weight_scales, bn_final_train_loss, '-o', label='batchnorm')
plt.legend()
plt.gca().set_ylim(1.0, 3.5)
plt.gcf().set_size_inches(15, 15)
plt.show()
说明 Batch normalization 可以减少坏初始化的影响
Batch normalization and batch size
# Batch normalization and batch size
def run_batchsize_experiments(normalization_mode):
np.random.seed(231)
# Try training a very deep net with batchnorm
hidden_dims = [100, 100, 100, 100, 100]
num_train = 1000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
n_epochs = 10
weight_scale = 2e-2
batch_sizes = [5, 10, 50]
lr = 10 ** (-3.5)
solver_bsize = batch_sizes[0]
print('No normalization: batch size = ', solver_bsize)
model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization=None)
solver = Solver(model, small_data,
num_epochs=n_epochs, batch_size=solver_bsize,
update_rule='adam',
optim_config={
'learning_rate': lr,
},
verbose=False)
solver.train()
bn_solvers = []
for i in range(len(batch_sizes)):
b_size = batch_sizes[i]
print('Normalization: batch size = ', b_size)
bn_model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization=normalization_mode)
bn_solver = Solver(bn_model, small_data,
num_epochs=n_epochs, batch_size=b_size,
update_rule='adam',
optim_config={
'learning_rate': lr,
},
verbose=False)
bn_solver.train()
bn_solvers.append(bn_solver)
return bn_solvers, solver, batch_sizes
batch_sizes = [5, 10, 50]
bn_solvers_bsize, solver_bsize, batch_sizes = run_batchsize_experiments('batchnorm')
plt.subplot(2, 1, 1)
plot_training_history('Training accuracy (Batch Normalization)','Epoch', solver_bsize, bn_solvers_bsize, \
lambda x: x.train_acc_history, bl_marker='-^', bn_marker='-o', labels=batch_sizes)
plt.subplot(2, 1, 2)
plot_training_history('Validation accuracy (Batch Normalization)','Epoch', solver_bsize, bn_solvers_bsize, \
lambda x: x.val_acc_history, bl_marker='-^', bn_marker='-o', labels=batch_sizes)
plt.gcf().set_size_inches(15, 10)
plt.show()