方程组求解的直接法与迭代法实现
方程组求解的直接法与迭代法实现
问题描述
我们的目的在于求解如下所示的方程组:
其中的 A 11 、 A 12 、 A 21 、 A 22 A_{11}、A_{12}、A_{21}、A_{22} A11、A12、A21、A22以及右端项 f f f以不同的的稀疏存储方式存在文件中。
我们需要完成的问题包括:
- 理解并描述 A 11 、 A 12 、 A 21 、 A 22 A_{11}、A_{12}、A_{21}、A_{22} A11、A12、A21、A22以及右端项 f f f的数据存储方式,其中 A 11 A_{11} A11是以CSR(compressed)方式存储,其余以COO(coordinate or IJ)方式存储。
- 设计一种数据存储方式来储存具有块结构的稀疏矩阵 A A A。
- 写一段程序读取 A A A的子块,并将其以设计好的结构存储为 A A A。
- 用MUMPS,SuperLU等方法来直接求解方程组。
- 选择和应用一种迭代方法来求解线性方程组,并提供随着迭代步的进行的收敛情况(和直接法做比较)。
- 基于你对这个线性系统的理解,设计一种有效的预条件子方法来加速迭代方法的收敛。
CSR和COO矩阵压缩稀疏存储方式说明
CSR:压缩稀疏行存储
N = 58324,M=99。
A 11 A_{11} A11稀疏存储文件说明:
- 第1行3个数:
行块数(58324),列块数(58324),非零块数(385766) - 第2行:
每一块小矩阵的规模(边长3) - 第3行:
每一块的flatten方式(0表示一行一行来) - 第4行:
记录非零矩阵块累计数(按行)的向量的元素个数(58325) - 第5~58329行(58325个):
表示非零矩阵块数目的累计值(IA),即后一个值减前一个值表示当前行的非零块个数。 - 第58330行:
非零块的个数(385766) - 第58331~444096行(385766个):
表示对应于(IA)的非零块的列标(JA,标号从0开始) - 第444097行:
非零元素块的元素个数综合(3471894) - 第444098~3915991行(3471894个):
非零元素位置对应的值
COO:坐标稀疏存储
A 12 A_{12} A12稀疏存储文件说明:
- 第1行3个数:
行数(174972),列数(99),非零元素(1148) - 第2到1149行(1148个):
行坐标,列坐标,值
A 21 A_{21} A21稀疏存储文件说明:
- 第1行3个数:
行数(99),列数(174972),非零元素(1100) - 第2到1101行(1100个):
行坐标,列坐标,值
A 21 A_{21} A21稀疏存储文件说明:
- 第1行3个数:
行数(99),列数(99),非零元素(99) - 第2到100行(99个):
行坐标,列坐标,值
f f f稀疏存储文件说明:
- 第1行:
列数(175071) - 第2到175072行(175071个):
位置和值
A A A的组装和存储
观察 A A A的四个子块以及右端项的存储方式,我们发现,除了 A 11 A_{11} A11使用CSR方式存储之外,其他部分用的都是COO的存储方式。一个简单的想法是,先把 A 11 A_{11} A11装成COO存储方式,在将几个子块读入,组装成 A A A,以COO的方式写入文件,以便备用。这个过程我用Matlab(Matlab 2014a 盗版)来实现。
A 11 A_{11} A11的从CSR格式转成COO格式并保存的代码如下:
clc
clear
%% 读入数据,只读第一列
filename = 'A11.dat';
delimiter = ' ';
formatSpec = '%f%*s%*s%[^\n\r]';
fileID = fopen(filename,'r');
dataArray = textscan(fileID, formatSpec, 'Delimiter', delimiter, 'MultipleDelimsAsOne', true, 'EmptyValue' ,NaN, 'ReturnOnError', false);
fclose(fileID);
A11 = [dataArray{1:end-1}];
clearvars filename delimiter formatSpec fileID dataArray ans;
%% 处理数据,转为COO格式,并保存
n = 174972;
IA = A11(5:58329,:);
nonzero_mat_num = IA(2:end)-IA(1:end-1);%共58324个
JA = A11(58331:444096,:);
JA = JA+1;%matlab的下标从1开始
values = A11(444098:3915991,:);
row1 = [174972 174972 3471894];
submat_sparse_store_row = [];
for i=1:58324
current_num = nonzero_mat_num(i);
submat_sparse_store_row(end+1:end+current_num,1) = repmat(i,current_num,1);
end
submat_sparse_store_col = JA;
sparse_X = [];
sparse_Y = [];
sparse_values = values;
for i=1:385766
ind_row = submat_sparse_store_row(i);
ind_col = submat_sparse_store_col(i);
[x,y] = meshgrid((ind_row-1)*3+1:(ind_row)*3,(ind_col-1)*3+1:(ind_col)*3);
x_temp = x;
y_temp = y;
x_flatten = x_temp(:);
y_flatten = y_temp(:);
sparse_X(end+1:end+9,1) = x_flatten;
sparse_Y(end+1:end+9,1) = y_flatten;
end
A11_sparse = sparse(sparse_X,sparse_Y,values);
A11_sparse(2000,2000)
sum(sum((A11_sparse ~= 0)))
data = [row1;sparse_X-1 sparse_Y-1 values];
save('A11_coo.dat','data','-ascii');%ps:save方式的存储会产生误差,但是速度快咯,anyway,问题不大
%dlmwrite('A11_coo.dat',data,'delimiter','\t','precision','%0.6e');
从四个子块组装为 A A A并以COO格式保存为A.dat的代码如下:
% 将四个系数矩阵拼成一个矩阵
clc
clear
%%
N = 58324;
M = 99;
n = 3*N;
m = M;
%%
load('A11_coo.dat');
load('A12.dat');
load('A21.dat');
load('A22.dat');
%%
A11_h = A11_coo(1,:);
T11 = A11_coo(2:end,:);
%%
A12_h = A12(1,:);
T12 = A12(2:end,:);
T12(:,2) = T12(:,2)+n;
%%
A21_h = A21(1,:);
T21 = A21(2:end,:);
T21(:,1) = T21(:,1)+n;
%%
A22_h = A22(1,:);
T22 = A22(2:end,:);
T22(:,1) = T22(:,1) + n;
T22(:,2) = T22(:,2) + n;
%%
A_header_num = A11_h(3) + A12_h(3) + A21_h(3) + A22_h(3);
A_header = [175071 175071 A_header_num];
T = [T11;T12;T21;T22];
A = [A_header;T];
%save('A.dat','A',''-ascii','-double');
%% 写入数据,第一行和第一列和第二列以int类型写入,第三列(除第一行),以双精度类型写入。
fileID = fopen('A.dat','w');
fprintf(fileID,'%6d %6d %6d\r\n',A(1,1),A(1,2),A(1,3));
%fprintf('%6d %6d %6d\n',A(1,1),A(1,2),A(1,3));
for k=1:size(A,1)-1
fprintf(fileID,'%d %d %1.6e\n',A(k+1,1),A(k+1,2),A(k+1,3));
%fprintf('%d %d %1.6e\n',A(k+1,1),A(k+1,2),A(k+1,3));
end
fclose(fileID);
%%
% B = sparse(A(2:end,1)+1,A(2:end,2)+1,A(2:end,3));
% B_full = full(B);
Matlab的back slash方法求解方程组
\符号求解方程组
既然用了Matlab,首先,一个自然的想法就是使用Matlab的\来求解方程组。使用的代码如下:
clc
clear
%% 导入A和f的数据
load('A.dat');
f_id = fopen('f.dat','r');
fgets(f_id);
formatSpec = '%d %f';
sizef = [2 Inf];
ff = fscanf(f_id,formatSpec,sizef);
fclose(f_id);
ff = ff';
f = ff(:,2);
%%
A_h = A(1,:);
T = A(2:end,:);
%%
AA = sparse(T(1:end,1)+1,T(1:end,2)+1,T(1:end,3));
u = AA\f;
%%
u_header = 175071;
u_mine = u;
save('u_mine.dat','u_mine','-ascii');
%% check result
E = u(1)-1.24456;
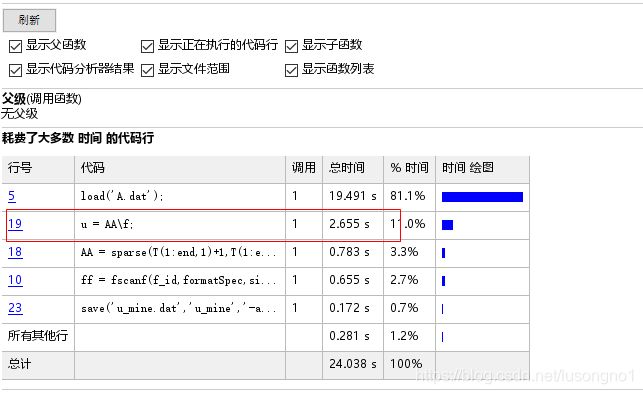
做个简单的计时,发现back slash求解大概需要2.655s。
求解的结果的前几个值如下:
我的计算机参数
自报一下家门,老电脑了,四核处理器,每个核心2.60GHz,单核每个时钟周期执行的浮点运算次数大约为25。
理 论 峰 值 速 度 = cpu 主 频 ∗ 每 个 时 钟 周 期 执 行 的 浮 点 运 算 次 数 ∗ 核 数 理论峰值速度=\text{cpu}主频*每个时钟周期执行的浮点运算次数*核数 理论峰值速度=cpu主频∗每个时钟周期执行的浮点运算次数∗核数
笔记本的峰值计算能力为256亿浮点运算/秒,具体如下:
制造商 : Intel
型号 : Intel® Core™ i5-3230M CPU @ 2.60GHz
速度 : 3.2千兆赫(GHz)
最低/最高速度/涡轮速度 : 1.2千兆赫(GHz) - 2.6千兆赫(GHz) - 3.2千兆赫(GHz)
恒速 : 2.6千兆赫(GHz)
峰值处理性能 (PPP) : 25.6数十亿浮点运算/秒(GFLOPS)
调整后的峰值性能 (APP) : 7.68WG
内核/处理器 : 2 个
线程/内核 : 2 个
类型 : 便携电脑
关于matlab内置算法的一个说明
关于matlab的backslash:对于稀疏矩阵的\(mldivide)方法求解,Matlab大多时候使用的是分解算法,如QR solver、diagonal solver、banded solver、(permuted)triangular solver、LU solver、Cholesky solver和LDLsolver等等。Matlab会自己进行条件判断,而根据矩阵情况选择合适的算法。
另外,查看了matlab的document,其对于稀疏矩阵的分解解法和迭代解法如下:
对于一般的方法,有一定的适用条件:比如说pcg用于处理Hermitian正定矩阵,minres一般用于处理Hermitian矩阵。
直接法求解(MUMPS, SuperLU,etc)
Matlab没有现成的MUMPS,SuperLU的求解器。怎么办?只能使用c中的相应的库来实现。当然,也可以利用Matlab和c或者Fortran的混编,毕竟MUMPS的SuperLU的包没有matlab版本的,那么又想用Matlab来调用,这么干也是可以的。
我第一个想到的是使用所里的phg来实现,因为它有相关的接口。我在ubuntu下安装了phg及其相关的依赖,用以调试程序,等到合适的时候,再将程序放到所里的科学计算集群(LSSC-IV)上去运行。
phg的方程组求解器接口调用
编写c程序,读入Matlab生成的A.dat和已有的f.dat文件,调用phg的解法器接口,进行求解。代码如下:
#include "phg.h"
#include
#include
#include
#include
int main(int argc, char *argv[])
{
/* Read data, including A and f. 先一次性把数据读进来,这样比较节省时间。*/
FILE *fp;
if ((fp = fopen("A.dat", "r")) == NULL)
{
printf("cannot find what you need,please check it!");
exit(0);
}
int m, n, numOfNonzero;
int i;
fscanf(fp, "%d%d%d", &m, &n, &numOfNonzero);
float *valuesOfA = (float*)malloc(sizeof(float)*numOfNonzero);
int *rows = (int*)malloc(sizeof(int)*numOfNonzero);
int *cols = (int*)malloc(sizeof(int)*numOfNonzero);
for (i = 0; i <= numOfNonzero - 1; i++)
{
fscanf(fp, "%d%d%f", &rows[i], &cols[i], &valuesOfA[i]);
}
fclose(fp);
if ((fp = fopen("f.dat", "r")) == NULL)
{
printf("cannot find what you need,please check it!");
exit(0);
}
int numOff;
fscanf(fp, "%d", &numOff);
double *valuesOff = (double*)malloc(sizeof(double)*numOff);
int *indexOff = (int*)malloc(sizeof(int)*numOff);
for (i = 0; i <= numOff - 1; i++)
{
fscanf(fp, "%d%lf", &indexOff[i], &valuesOff[i]);
//printf("%d,%0.15e\n", indexOff[i], valuesOff[i]);
}
fclose(fp);
/*finish reading data. */
// printf("%d,%d,%0.6e\n", rows[0], cols[0], valuesOfA[0]);
// printf("%d,%0.15e\n", indexOff[0], valuesOff[0]);
// getchar();
//读如的数据存放在rows、cols、valuesOfA和indexOff以及valuesOff中。
SOLVER *solver;//创建解法器对象
MAT *A;
MAP *map;
// MPI_Comm comm;
// phgInitSetComm(comm);
phgInit(&argc,&argv);
// printf("phgComm=%d",phgComm);
map = phgMapCreateSimpleMap(phgComm,-1,175071);
A = phgMapCreateMat(map,map);
int numOfNonzeroInA = 3474241;
for (i = 0; i <= numOfNonzeroInA - 1; i++)
{
int row = rows[i];
int col = cols[i];
float value = (float)valuesOfA[i];
//printf("row=%d,col=%d,value=%f\n",row,col,value);
phgMatAddGlobalEntry(A, row, col, value);
//printf("debug: program comes here……\n");
}
solver = phgSolverMat2Solver(SOLVER_DEFAULT,A);
solver->verb = 1;
int N = 175071;
//printf("debug: program comes here……%f%f",indexOff[100],valuesOff);
// phgVecAddGlobalEntries(u,0,N,indexOff,valuesOff);
phgVecDisassemble(solver->rhs);
for (i = 0; i <= N - 1; i++)
{
int index = indexOff[i];
float value = valuesOff[i];
value = (float)value;
// printf("i=%dindex=%dvalue=%f",i,index,value);
// getchar();
// phgMatAddGlobalEntry(A, row, col, value);
phgSolverAddGlobalRHSEntry(solver,index,value);
}
VEC *u_h;//定义VEC对象存放解
u_h = phgMapCreateVec(map,1);
// phgVecDisassemble(u_h);
// const char *var_name = "f_out";
// const char *file_name = "f_out";
// phgVecDumpMATLAB(solver->rhs,var_name,file_name);
// var_name = "A_out";
// file_name = "A_out";
// phgMatDumpMATLAB(solver->mat,var_name,file_name);
phgSolverVecSolve(solver, 0, u_h);//求解
/* const char *var_name = "u_h";
const char *file_name = "u_mine";
phgVecDumpMATLAB(u_h,var_name,file_name);
*/
return 0;
}
/*自由度对象赋值*/
/* //solver = phgSolverCreate(SOLVER_DEFAULT, u_h, NULL);//定义解法器
for (int i = 0; i <= numOfNonzero - 1; i++)
{
int row = rows[i];
int col = cols[i];
float value = (float)valuesOfA[i];
phgSolverAddGlobalMatrixEntry(solver, row, col, value);
}
printf("debug: program comes here……\n");
for (int i = 0; i <= numOfNonzero - 1; i++)
{
int index = indexOff[i];
float value = (float)valuesOff[i];
phgSolverAddGlobalRHSEntry(solver, index, value);
}
phgSolverSolve(solver, TRUE, u_h, NULL);//求解
//SIMPLEX *e;
// const FLOAT lambda[];
// FLOAT *values;
// phgDofEval(u_h, e, lambda, values);//不足的输入要补全。
// phgPrintf("first value of u is : %lf\n", *values);//打印结果
phgSolverDestroy(&solver);//销毁解法器对象
*/
编译生成可执行文件后,我们来命令行传入参数来调用phg中的解法器来求解这个 方程组。phg中预装的解法器接口有: “pcg”, “bicgstab”, “gmres”, “lgmres”, “preonly”, “aps”, “2grid”, “ams”, “gather”, “asm”, “smoother”, “hypre”, “petsc”, “mumps”, “superlu”, “minres”, "diagonal"等。
按照要求,我现在想调用mumps和superlu求解。
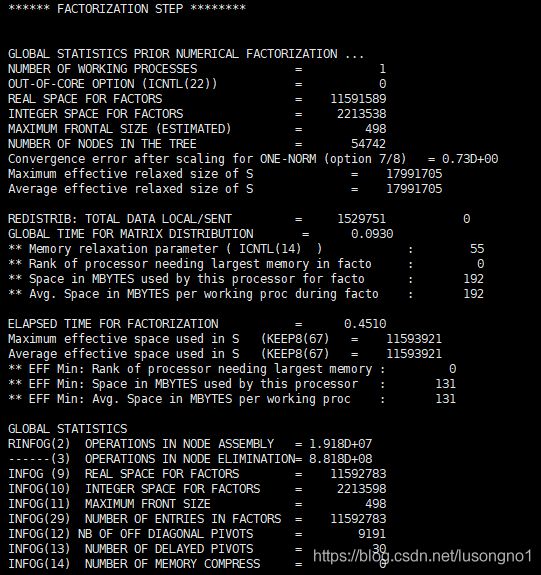
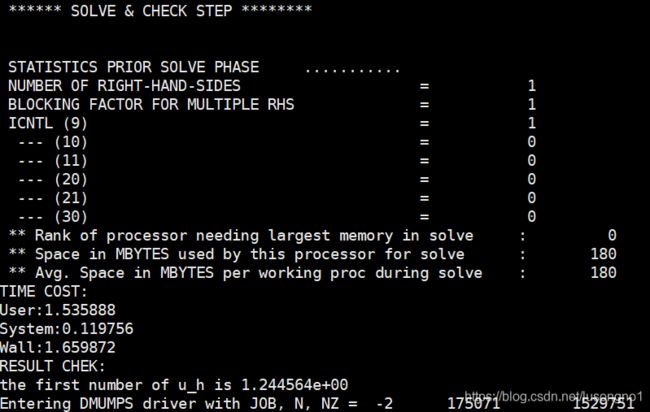
基于phg平台的mumps方法求解
phg提供的mumps的接口,提供了以下的参数:
在矩阵的性质中,我们给它指定非对称,其他的参数保持默认。使用如下所示命令行参数执行可执行文件:
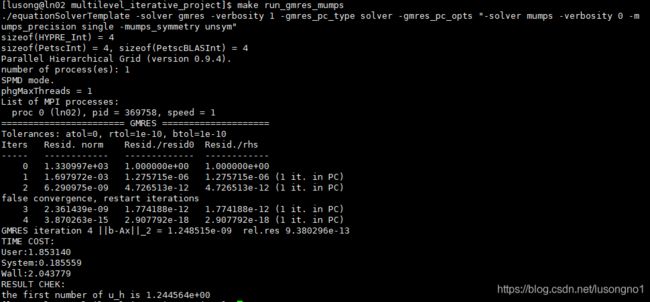
./equationSolverTemplate -solver mumps -mumps_symmetry unsym
结果如下:
可以看到,打印出来的墙上时间为1.66s,比Matlab略快一些。
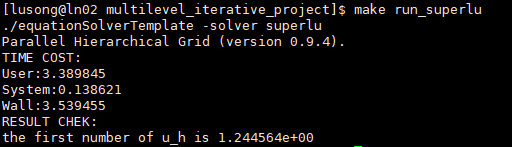
基于phg平台的superlu方法求解
查看superlu的参数帮助信息如下:
我选择保持默认。使用如下命令执行可执行程序。
./equationSolverTemplate -solver superlu
结果如下:
消耗的墙上时间约为3.54s,比MUMPS方法略慢一些。
Anyway,我们由直接法,不管是Matlab的back slash还是MUMPS抑或是SUPER LU,我们用直接法得到了一个可以在迭代法中作为标准的近似真解。我们可以把这个解保存下来,下面再使用这个解来作为迭代法收敛性分析的一个标准。
迭代方法设计与求解
A A A矩阵性态的观察
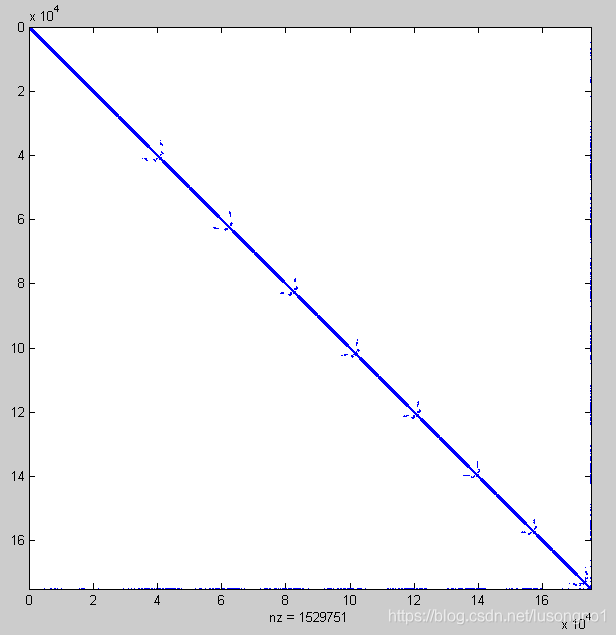
使用Matlab的spy函数,我们来观察一下矩阵 A A A的分布,结果如下:
看起来是个对角矩阵,而且很稀疏。我们再通过sum(sum((A - A')))判断,发现 A A A并不是对称的,只不过是在外形上看起来有些对称(事实上,在外形上也不是对称的)。进一步,我们通过[r,p]=chol(A)判定,它并不是正定的(非对称意义下的正定)。
所以,这是一个非零元素基本上都集中在对角线以及两条边上的没有特别好的性质的稀疏矩阵。
方法的选择
我们可以设计和使用多层迭代方法来求解。时间的原因,我们依然调用别人已经写好的包,而不自己动手完成这个过程。能使用的包就比较多了,比如由张晨松老师等人编写维护的FASP的包,下载地址,另外还有Matlab内置的共轭梯度,残差法等等。
因为这个矩阵的在性质上,好像除了看起来有点对称以及稀疏之外,没有太好的性质。所以,我想采用GMRES方法求解。GMRES中文叫广义极小剩余法,它是上世纪末到本世界初被人们认为是求解大型稀疏非对称线性方程组的最有效的方法之一。Matlab有gmres内置函数,基于重启动的gmres方法。我想用的依然是phg的内置的gmres算法。
为了加快的速度,我用的是预条件子的GMRES方法。phg中gmres solver的参数如下所示。
预条件子的选择,使用GMRES,我的预条件子选择了两个:一个是MUMPS作为预条件子,另一个是ASM(加性 Schwarz作为预条件子),并且在ASM预条件子中使用单精度的稀疏直接求解器MUMPS求解子区域问题。
基于MUMPS预优的GMRES方法
指定用单精度的MUMPS解法器做为GMRES的预条件子。我在 Makefile中定义的命令行参数如下:
上图中,gmres_pc_type 中的 “solver” 参数表示在 GMRES 每步迭代中调用另一个解法器做为预条
件子,而 -gmres_pc_opts 选项则用来设定预条件子解法器及参数。
运行的结果如下:
使用单个进程,设定atol=0, rtol=1e-10, btol=1e-10。从结果中可以看出,迭代2次之后,有一次重启动。迭代4次残差相对值达到了-18次方量级的。墙上时间消耗时间为2.04s。收敛速度是非常快的。这是在最外层的迭代,内层表现我们就不往里看了。
基于ASM预优(ASM中使用MUMPS求解子区域问题)的GMRES方法
指定使用 GMRES 迭代、ASM (加性 Schwarz)预条件子,并且在 ASM 预条件子中使用单精度的稀疏直接求解器 MUMPS 求解子区域问题。
在Makefile中定义的参数列表如下:
结果如下:
经过一次的迭代(最外层的求解器),误差(相对残差)达到了e-14量级的。墙上时间消耗为1.81s。
使用Matlab的gmres内置函数求解
我们考虑一种比较简单的情况,即使用不完全LU预优分解,不采用重启动技术,我们来看看它的收敛表现。
这一次,我们不用残差来衡量误差,而使用直接法得到的解作为一个参考标准。写一段简单的matlab脚本如下,用来调用matlab的gmres内置函数。
clc
clear
%% 导入A,f和真解u
load('A.dat');
%A_h = A(1,:);
T = A(2:end,:);
AA = sparse(T(1:end,1)+1,T(1:end,2)+1,T(1:end,3));
A = AA;
f_id = fopen('f.dat','r');
fgets(f_id);
formatSpec = '%d %f';
sizef = [2 Inf];
ff = fscanf(f_id,formatSpec,sizef);
fclose(f_id);
ff = ff';
f = ff(:,2);
load u_mine.dat
u = u_mine;
clear AA f_id ff formatSpec sizef T u_id uu;
%%
[L,U] = ilu(A,struct('type','ilutp','droptol',1e-6));
l = length(f);
tol = 1e-12;
maxit = 20;
b = f;
x0 = zeros(l,1);
errors = [norm(x0 - u)/norm(u);];
for i = 1:maxit
[x0,fl0,rr0,it0,rv0] = gmres(A,b,1,tol,1,L,U,x0);
errors(end+1) = norm(x0 - u)/norm(u);
end
st = 4;
semilogy(st:maxit,errors(st+1:end),'-o');
xlabel('Iteration number');
ylabel('Relative Error');
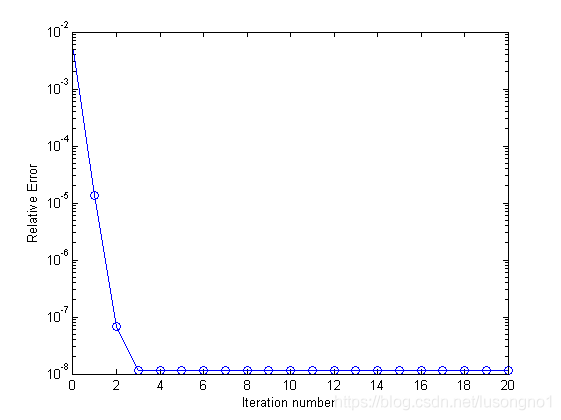
结果如下:
这里定义的误差为 Error = ∣ ∣ u − u h ∣ ∣ 2 / ∣ ∣ u ∣ ∣ 2 \text{Error} = ||u-u_h||_2/||u||_2 Error=∣∣u−uh∣∣2/∣∣u∣∣2。这里的u,用的是直接法得出来的解。可以看得出来,使用不完全LU分解做预优的GMRES方法,只要两三步就达到比较高的精度了。也容易看出,迭代到第4步,误差就降低到了e-8量级的。另外,这个过程也不是单调的,在第5步到第6步,误差有一个非常微小的升高。