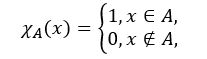模糊集与模糊聚类

数据挖掘讲课任务梳理：   

目录

西大数据挖掘讲课任务梳理：   

模糊集的历史

模糊集基本概念

模糊集定义

隶属函数

模糊集的表示方法

模糊集的运算

模糊集的特性

模糊关系

模糊逻辑与模糊推理

数据挖掘中的模糊方法:

模糊聚类

---

模糊集的历史

19世纪以前，是传统逻辑的时代，主要是就是亚里士多的的精确数学，后来柏拉图反对这种非此即彼的思维方法，他认为真假之间应该存在一种灰色地带，经过不断探索之后，1965年，扎特创立了一种描述模糊现象的方法，模糊集合论，并进行了进一步的研究。

其实，在我们的日常生活中存在着很多模糊的现象，比如“好与坏，暖和、很大”等概念，但是这些概念在我们的头脑中有一个标准并被人们普遍接受。

  

模糊集基本概念

模糊集定义

接下来，在介绍模糊集的定义之前，先介绍几个简单的概念：首先，论域表示我们处理某个问题是我们所讨论的限制范围，集合表示在论域中具有某个属性的事物的集合。比如，我们讨论白梨与鸭梨可以分别表示为两个集合，而梨就可以表示为论域。

对于特征函数，我们以二值集合为例，假设在论域X中，A是论域X中的一个集合，对于任意的x属于X，我们会有，x要么是A中的元素，要么不是A中的元素，因此，由集合A可以确定一个映射，??::?→{0,1},因此，映射函数可以用下面的公式表示

                                                                      

如果x是A 中的元素，那么就定义为1，如果x不是A中的元素，就用0表示，这就是A的特征函数。隶属度，就表示元素x属于A的可能性大小。，最后，我们引出模糊集的概念，假定论域为X，x是X种的一个特定元素，那么模糊集A有一个隶属度映射函数刻画：??:?→[0,1]。?? 就称为隶属函数，??(?)称为?对?的隶属度.

                

那么模糊集与传统的经典集合是什么关系呢？模糊集表示的是一个抽象的概念，我们通过uA(x) 来表示一个元素属于A的确定性，的值越接近1表示x隶属于A的可能性越大，相反，越低，而对于二值集合而言，或者为1，即完全隶属于A，或者为0，即完全不属于A，因此，可以认为二值集合是模糊集合的一种特殊情况。

                    

隶属函数是模糊集合的实质，隶属函数可以是任何的类型的函数，根据具体的模糊集特征进行定义。但需要满足以下一些约束：1......,2......,3.......

隶属函数

                         

模糊集的表示方法

可以对离散（有限）域或者连续（无限）域定义模糊集。模糊集一般有三种表示方法。扎德表示，序偶表示法，以及隶属函数表示法。隶属函数表示法就是直接使用隶属函数来表示模糊集。我们用扎德表示法的时候：对于离散级，我们使用求和符号表示，如下式，....，式中的+/表示的是分隔符号，这里的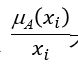表示x隶属于A的程度。对于无限集我们用这个式中表示。

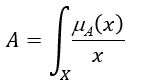当论域为有限集的时候，定义在论域上的模糊集还可以用序偶的形式表示，即

                                

这就是模糊集的三种表示方法，下面我们举个简单的例子进行说明：

                

模糊集的运算

接下来我们介绍模糊集合的一些基本的运算规则：我们首先介绍一下经典集合的运算：属于，交、并、补、相等。对于模糊集，两个模糊集的相等不能仅由两个集合的元素相等而判断，还应该确保两个集合中元素对应的隶属度也是相同的，同样，元素的包含关系也是一样的。对于模糊集的交，实现交的算子称为t范数，最常用的交算子是最小算子，模糊集的并，实现并的算子称为s范数，最常用的算子是最大算子。二值集合的补是包含除该集合之外的整个域中的其他元素，但是对于模糊集，一个集合A 的补包含集合A 中的所有元素，但隶属度不同。因此，模糊集A 与他的补的交集不等于空集，并不等于整个域X。下面的四个图是就是表示模糊集基本运算的示意图。

                               

对于模糊集合之间的运算规律而言，除了我们刚刚提到的互补律不成立之外，其他运算规律都是与二值函数的运算规律一样成立的。

模糊集的特性

接下来我们介绍模糊集的几个特性，首先最重要的就是λ-截集。在论域X中，给定一个模糊集合A，由对于A的隶属度大于某一水平值λ（阈值）的元素组成的集合，叫做该模糊集合的λ水平截集。用公式可以描述如下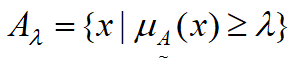：         （λ-截集）A =    ​​​​​​​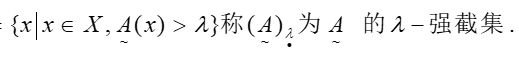

正规化，一个集合A 中具有隶属度为1 的元素，那么A就是正规。

高度就是表示一个模糊集隶属度的上确界，，也就是属于A的集合中隶属度的值最大为多少。

支持 就是所有属于模糊集A中隶属度大于0 的集合。

核 表示模糊集A中所有隶属度为1的元素组成的集合。

                                   

基数 ：对于二值函数而言基数就是集合元素的个数，对于模糊集而言，有限域中：基数是属于模糊集A的所有元素对应的隶属度的和。

归一化： 用模糊集的高度除以隶属函数就可以实现对模糊集的归一化。

                                    

我们经常会混淆模糊与概率的概念，接下来就简单的介绍一下概率和模糊的区别与相同点。相同点是都在[0,1]之间表示不确定性。不同点是概率表示的确定性程度是在事件发生之前，而模糊在事件发生之后任然有意义。概率假定事件之间是相互独立的，而且是在假定任何事件都已知的封闭模型中，概率表示的是一个事件发生频度的度量。模糊按照隶属函数度量，而且也不需要假定事情已知。这就是概率和模糊的区别。因此，模糊并不是概率，概率也并不是模糊。例如下面两个例子。

                                               

模糊关系

关系也是集合中一个重要的概念。它反应了不同集合之间的相互关系。模糊关系中，例如母子之间是否长得像？家庭是否和睦之类的，都属于模糊关系。我们假设x是论域U中的元素，y是论域V中的元素，U到V的一个模糊关系是指定义在上的一个模糊子集，其隶属度    代表x和y对于该模糊关系的关联程度。 ​​​​​​​例如，.......

模糊关系也经常用矩阵的形式表示，U到V的模糊关系可以用矩阵描述为.....。因此，上例中的模糊关系又可以用矩阵描述为：........。

                                            

模糊关系的合成，就类似于矩阵的乘法，但是运算符不是取乘号与加号而是取交和并。

                                       

我们通过一个例题来进一步熟悉。

                                    

下面介绍模糊变换

                                            

我们同样通过一个例子来进行说明。

                                                             

模糊逻辑与模糊推理

扎德将模糊逻辑定义为一个逻辑系统，该系统是多值逻辑的一个扩展。在模糊逻辑中最为重要的两个概念就是语言学变量和模糊规则if-then 。

首先，我们介绍语言变量，语言变量来源于自然语言中词汇这句子，并具有值，但是它的取值不是通常的数，而是用模糊语言来表示。例如，对于年龄这个模糊变量，他的取值为年幼，年轻，年老等集合。我们在定义一个语言变量的时候要包括以下几个内容：一是变量名称，比如“速度”，然后定义变量的论域，例如定为【0,200】km/h然后定义语言值，在论域[0，200]上定义变量的语言值为 {慢，中，快}；最后定义每个模糊集合的隶属函数：u（快）、u(中)、u（慢）。

                                                                  ​​​​​​​

模糊规则

模糊规则，对于一般的模糊系统，系统的动态行为由一组模糊规则描述，这些规则是基于其领域中人类专家的知识和经验。这部分与我们之前学过的专家系统很类似，因此，我们只做简单的介绍。模糊规则一般表示为：  if  前提  then  结论。这里的前提和结论都是包含语言变量的命题。含有多个前提条件的称为多维模糊规则，可以表示为：如果u1是A1，且u2是A2，…，且um是Am，则v是B。

                             

模糊推理

模糊推理我们简单的介绍通过模糊关系进行模糊推理，推理的合成规则CRI法。推理合成规则法关键有两步，一步是根据模糊规则到处模糊关系矩阵R，然后是模糊关系的合成运算。我们已知一个前提是：。。。另一个前提是：，，，我们要得出结论y是B’。也就是如图所示。具体实现时，我们先根据前提1 求A--->B 的关系矩阵，然后利用前提2 进行模糊关系的合成运算，得到y.具体的合成运算的规则前面已经介绍，在此就不再展开。关于模糊关系矩阵元素的计算，我们采用玛达尼方法进行计算，具体如下，隶属函数就可以表示为：。

                                ​​​​​​​

例题：

                                             

                                               

数据挖掘中的模糊方法:

这部分的介绍与前面的相对应进行讲解。

               

模糊聚类

最后，我们介绍一下模糊聚类。目标函数中c表示c类，n表示样本的数量，m为加权指数，一般取1.5-3.5 。u表示隶属函数，d用于计算样本点与中心点之间的欧几里德距离，通过这个公式，我们就可以计算每个样本点属于哪一类。对于目标函数的求解，我们可以使用拉格朗日乘子法进行求解，对所有输入参量求导，使式达到最小的必要条件为：u...c.....

最终得到隶属函数与聚类中心。dij与dkj都是表示距离。

                                

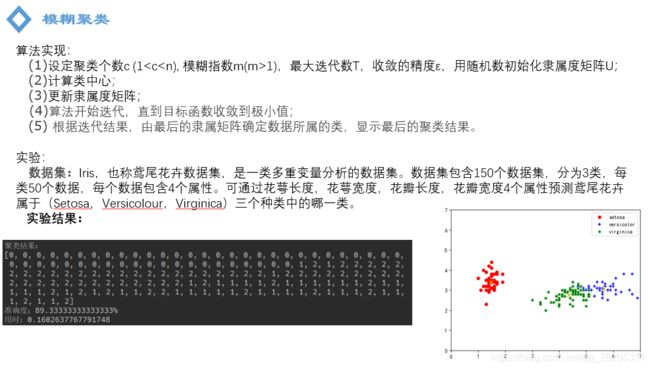
模糊C均值聚类算法是一个简单的迭代过程。在批处理方式运行时，FCM用下列步骤确定聚类中心ci和隶属矩阵U[1]：......用值在0，1间的随机数初始化隶属矩阵U,计算c个聚类中心，计算价值函数。如果它小于某个确定的阀值，或它相对上次价值函数值的改变量小于某个阀值，则算法停止。

实验中我们使用的是iris数据集，这个数据集.........通过算法我们的出了聚类的结果，0,1,2就表示聚类的类别，我们可以看到，0类都标记正确，1类有13个错误标记，2类有3个标记错误。因此我们得到最终的聚类准确率为89.33%，右图是横纵坐标分别为特征2和特征3时对应的聚类结果。

                                 ​​​​​​​

 

模糊聚类代码：

https://download.csdn.net/download/qq_28266311/11022838