排序算法介绍与Python实现

非线性排序算法

非线性排序算法有冒泡排序，选择排序，归并排序和快速排序。前两者时间复杂度为$O(n^2)$，适用于小的数据集，实现难度较低；而后两者时间复杂度为$O(nlogn)$，适用于普遍的中型数据集，很多编程语言的底层排序函数都基于这两者实现。，下面主要介绍归并排序和快速排序。

归并排序

首先将数组从中间分为两部分，然后再对这两部分分别进行排序，最后再将这两个数组合并，因此利用递归的思想，可以很容易实现归并排序。即将原数组进行不断分割，最后每一部分都是两个数，对其进行排序后，再将这一个个排序后的小数组进行合并，最终可以得到一个有序的数组。

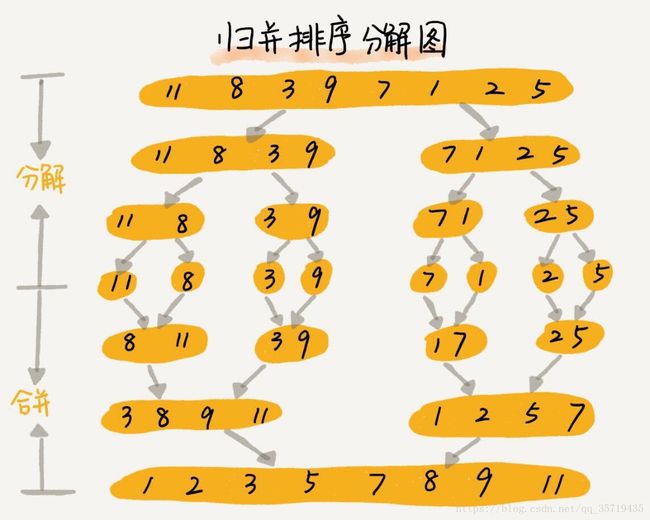
Python实现代码如下

def merge_sort(L):
    n = len(L)
    merge_l = merge_sort_c(L,0,n-1)
    return merge_l
    
def merge_sort_c(L,p,r):
    if p==r:
        return L[p:r+1]
    q = (p+r)//2
    left = merge_sort_c(L,p,q)
    right = merge_sort_c(L,q+1,r)
    ##sort and merge
    i,j = 0,0
    merge_l = []
    while i<len(left) and j < len(right):
        if left[i]<=right[j]:
            merge_l.append(left[i])
            i += 1
        else:
            merge_l.append(right[j])
            j += 1
    if i<len(left):
        merge_l += left[i:]
    else:
        merge_l += right[j:]
    return merge_l

l = [1,234,4,4,2,3,5,643,1,2,2,34]
print(merge_sort(l))

可以看到，归并排序先将原数组分割，再进行排序合并，是一个从下而上的操作。
归并排序是稳定的排序算法，且时间复杂度为O(nlogn)，但由于在合并操作时用到了额外的数组，因此是非原地排序算法。

快速排序

快速排序又称“快排”，有点类似归并排序，但又完全不一样。
快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot的。

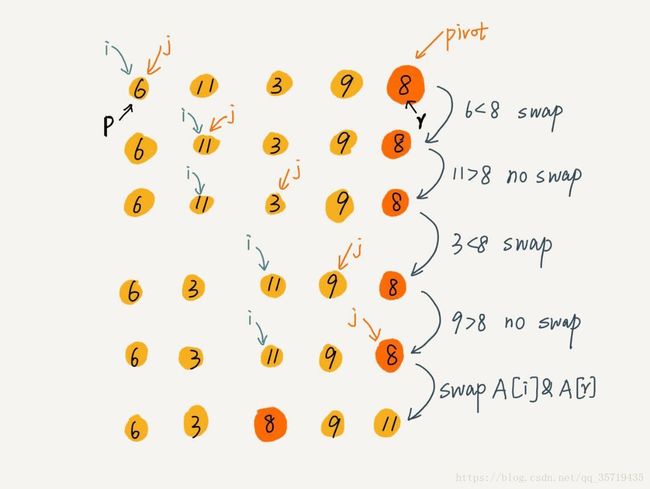
利用递归的思想，可以很容易写出快排的实现。下面是Python实现，一种是非原地排序的实现，一种是原地排序的实现。

def quick_sort(L):
    #非原地排序
    if len(L)<2:
        return L
    else:
        pivot = L[0]
        left = [i for i in L[1:] if i<=pivot]
        right = [i for i in L[1:] if i>pivot]
        return quick_sort(left)+[pivot]+quick_sort(right)

快排平均时间复杂度为O(nlogn)，极端情况下最坏时间复杂度会退化为$O(n^2)$。

线性排序算法

对于大型数据集，非线性排序算法速度较慢，此时可考虑线性时间复杂度的排序算法，时间复杂度为$O(n)$，此类算法由一定的适用条件，下面主要介绍桶排序和计数排序。

桶排序

对于较大型的数据集，直接应用快排，实现起来速度会较慢。桶排序采用分治的思想，将大型数组均匀的分为m个桶，将数组拆分为m个较小的数组，然后再对每个桶分别利用快速排序进行排序。

下面分析为什么桶排序时间复杂度为线性的：

假设要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近$O(n)$。

尽管桶排序具有线性的时间复杂度，但是有较为严苛的适用条件：

1. 要排序的数据需要很容易的能划分为m个桶，并且每个桶具有天然的大小顺序。
2. 数据在各个桶中的分布是均匀的。考虑极端情况，所有数据都在一个桶里，桶排序退化为$O(nlogn)$的快排。

计数排序

计数排序是桶排序的一种特殊情况，但又有一些不同。计数排序适用于数据量大，而数据范围不大的数组，比如0-750分，几十万考生的高考分数排序。假设数组的最大值为k，那么便将数组分为k个桶，每个桶内的数据都是相等的，因此省去了桶内排序时间。计数排序的主要思想如下：
假设数组大小为n，最大值为k。将数组分为k个桶，记桶数组为L。L的索引代表着数值，L的值代表着该索引对应的值在原数组中的出现次数。对L累计求和，则L[j]代表着原数组中有L[j]个数小于j，那么此时便可把j放在第L[j]个位置。
直接看代码，Python实现如下：

def count_sort(L):
    n = len(L)
    range_k = max(L)+1
    count_array = [0]*range_k
    for i in L:
        count_array[i] += 1
    #calculate cumsum
    for i in range(1,range_k):
        count_array[i] = count_array[i-1]+count_array[i]
    sort_array = [0]*n
    for i in L[::-1]:
        index = count_array[i]-1
        sort_array[index] = i
        count_array[i] -= 1
    return sort_array

L = [2,5,3,0,2,3,0,3]
print(L)
print(count_sort(L))

小结

由以上可以看到，归并排序是自下而上进行排序，而快排是自上而下，刚好相反。

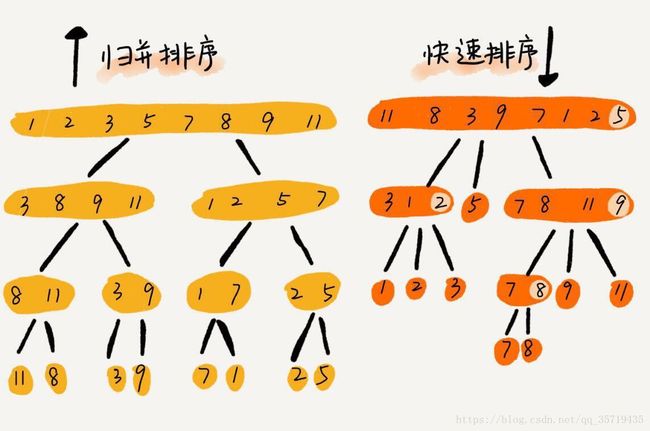
对于这两个排序算法，可以进行以下优化：

1. 快排中pivot的选择
   原先是利用第一个或最后一个数作为pivot，可利用三数选择法，选择首中尾三个数进行排序，取中间数作为pivot；或可随机选择pivot，这样在概率层面上不好最好也不会最差。

2. 栈溢出问题
   在递归调用时，若数据量过大，则会造成系统的栈溢出（因为递归调用相当于将函数压入栈），解决方法可自定义栈，将递归函数压入自定义栈。

桶排序和计数排序由于线性时间复杂度适用于大型数据集，但适用条件非常有限 ，需要谨慎使用。一般桶排序适用于外部排序中，即数据存储在外部磁盘中，数据量较大而内存有限，利用分治的思想可以解决。而计数排序在处理大型小范围数据排序特别有效，需要深刻理解。

算法	时间复杂度	稳定排序算法	原地排序算法
归并排序	O(nlogn)	Yes	No
快速排序	O(nlogn	No	Yes
桶排序	O(n)	Yes	No
计数排序	O(n)	Yes	No