Pytorch VOC2012(Faster RCNN)
目录
- Faster RCNN基本结构
- 1 Conv layers
- 2 Region Proposal Networks(RPN)
- 2.1 Anchors
- 2.2 RPN的真值与预测量
- 2.3 RPN卷积网络
- 2.4 RPN真值的求取
- 2.5 损失函数的计算
- 2.6 NMS与生成Proposal
- 2.7 筛选Proposal得到RoI
- 3 RoI pooling层
- 3.1 RoI Pooling简介
- 3.2 RoI Align简介
- 4 全连接RCNN模块
本篇文章介绍了Faster RCNN的基本原理和思路,参考地址为一文读懂Faster RCNN
Faster RCNN基本结构
经过R-CNN和Fast RCNN的积淀,Ross B. Girshick在2016年提出了新的Faster RCNN,在结构上,Faster RCNN已经将特征抽取(feature extraction),proposal提取,bounding box regression(rect refine),classification都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。
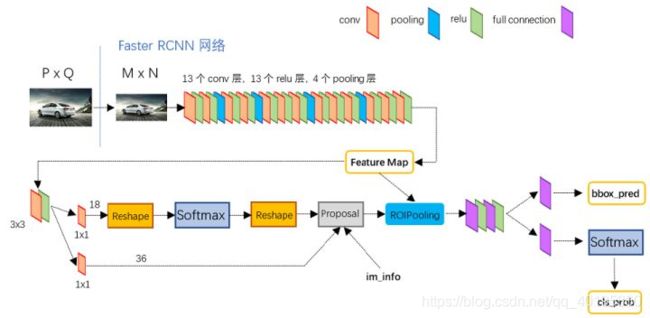
依作者看来,如图1,Faster RCNN其实可以分为4个主要内容:
- Conv layers。作为一种CNN网络目标检测方法,Faster RCNN首先使用一组基础的conv+relu+pooling层提取image的feature maps。该feature maps被共享用于后续RPN层和全连接层。
- Region Proposal Networks。RPN网络用于生成region proposals。该层通过softmax判断anchors属于positive或者negative,再利用bounding box regression修正anchors获得精确的proposals。
- Roi Pooling。该层收集输入的feature maps和proposals,综合这些信息后提取proposal feature maps,送入后续全连接层判定目标类别。
- Classification。利用proposal feature maps计算proposal的类别,同时再次bounding box regression获得检测框最终的精确位置。
所以本文以上述4个内容作为切入点介绍Faster R-CNN网络。
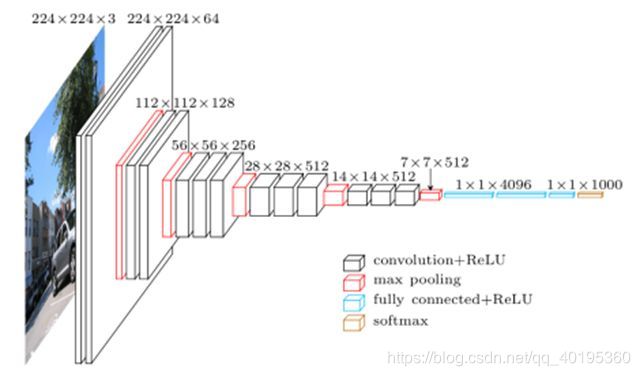
图2展示了python版本中的VGG16模型中的网络结构,可以清晰的看到该网络对于一副任意大小PxQ的图像,首先缩放至固定大小MxN,然后将MxN图像送入网络
- Conv layers中包含了13个conv层+13个relu层+4个pooling层(其实就是VGG16的网络结构);
- RPN网络首先经过3x3卷积,再分别生成positive anchors和对应bounding box regression偏移量,然后计算出proposals;
- Roi Pooling层则利用proposals从feature maps中提取proposal feature送入后续全连接和softmax网络作classification
- classification分类proposal到底是什么类别,同时再次bounding box regression获得检测框最终的精确位置。
注:
本文不会讨论任何关于R-CNN家族的历史,分析清楚最新的Faster R-CNN就够了,并不需要追溯到那么久。实话说我也不了解R-CNN,更不关心。有空不如看看新算法。
1 Conv layers
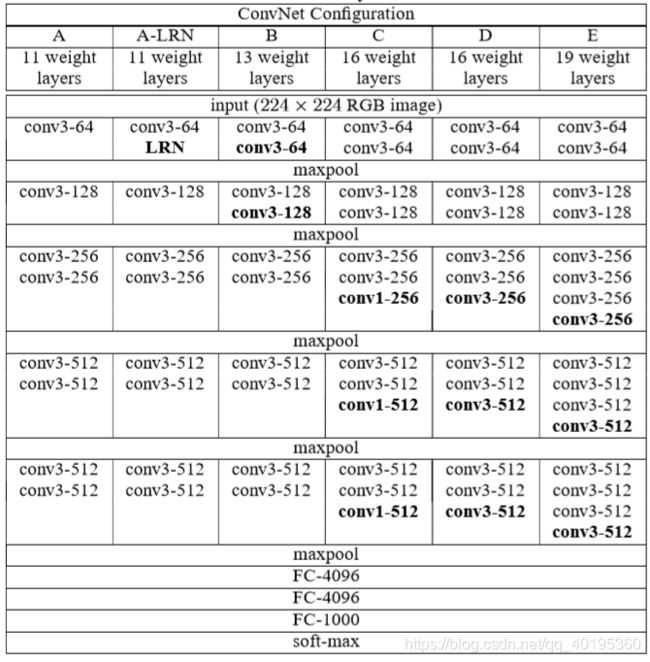
Conv layers包含了conv,pooling,relu三种层。以python版本中的VGG16模型中的网络结构为例(如图3),Conv layers部分共有13个conv层,13个relu层,4个pooling层(如图4)。
这里有一个非常容易被忽略但是又无比重要的信息,在Conv layers中:
- 所有的conv层都是:kernel_size=3,pad=1,stride=1,所以conv层不改变输入和输出矩阵大小;
- 所有的pooling层都是:kernel_size=2,pad=0,stride=2 ,所以这样每个经过pooling层的MxN矩阵,都会变为(M/2)x(N/2)大小
总结:conv和relu层不改变输入输出大小,只有pooling层使输出长宽都变为输入的1/2。那么,一个MxN大小的矩阵经过Conv layers固定变为(M/16)x(N/16)!这样Conv layers生成的feature map中都可以和原图对应起来。
2 Region Proposal Networks(RPN)
经典的检测方法生成检测框都非常耗时,如OpenCV adaboost使用滑动窗口+图像金字塔生成检测框;或如R-CNN使用SS(Selective Search)方法生成检测框。而Faster RCNN则抛弃了传统的滑动窗口和SS方法,直接使用RPN生成检测框,这也是Faster R-CNN的巨大优势,能极大提升检测框的生成速度。
RPN部分的输入、输出如下:
- 输入:feature map、物体标签,即训练集中所有物体的类别与边框位置。
- 输出:Proposal、分类Loss、回归Loss,其中,Proposal作为生成的区域,供后续模块分类与回归。两部分损失用作优化网络。
2.1 Anchors
理解Anchor是理解RPN乃至Faster RCNN的关键。Faster RCNN先提供一些先验的边框,然后再去筛选与修正,这样在Anchor的基础上做物体检测要比从无到有的直接拟合物体的边框容易一些。
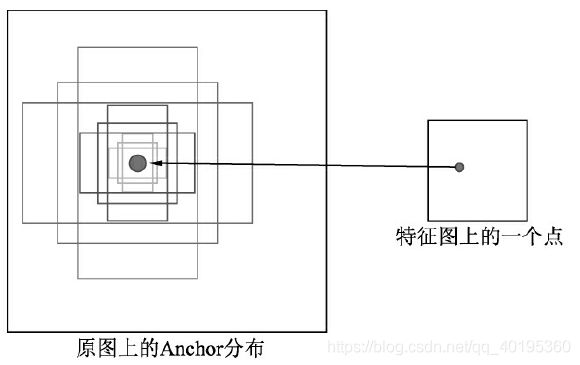
Anchor的本质是在原图大小上的一系列的矩形框,但Faster RCNN将这一系列的矩形框和feature map进行了关联。具体做法是,首先对feature map进行3×3的卷积操作,得到的每一个点的维度是512维,这512维的数据对应着原始图片上的很多不同的大小与宽高区域的特征,这些区域的中心点都相同。如果下采样率为默认的16,则每一个点的坐标乘以16即可得到对应的原图坐标。
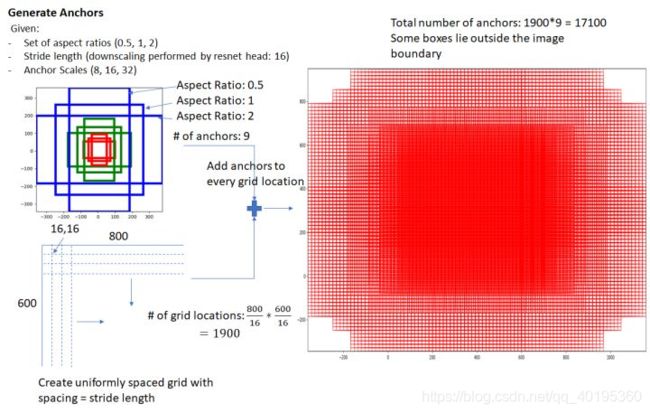
为适应不同物体的大小与宽高,在作者的论文中,默认在每一个点上抽取了9种Anchors,具体Scale为{8,16,32},Ratio为{0.5,1,2},将这9种Anchors的大小反算到原图上,即得到不同的原始Proposal,如图6所示。而后通过分类网络与回归网络得到每一个Anchor的前景背景概率和偏移量,前景背景概率用来判断Anchor是前景的概率,回归网络则是将预测偏移量作用到Anchor上使得Anchor更接近于真实物体坐标。
那么这9个anchors是做什么的呢?借用Faster RCNN论文中的原图,如图7,遍历Conv layers计算获得的feature maps,为每一个点都配备这9种anchors作为初始的检测框。这样做获得检测框很不准确,不用担心,后面还有2次回归可以修正检测框位置。
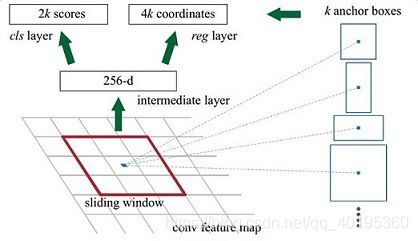
解释一下上面这张图的数字。
- 在原文中使用的是ZF Net(ILSVRC2013分类任务的冠军,使用反卷积对CNN的中间特征图进行可视化分析,通过分析特征行为找到提升模型的办法,微调Alexnet提升了表现。)其Conv Layers中最后的conv5层num_output=256,对应生成256张特征图,所以相当于feature map每个点都是256-dimensions
- 在conv5之后,做了rpn_conv/3x3卷积且num_output=256,相当于每个点又融合了周围3x3的空间信息(猜测这样做也许更鲁棒?反正我没测试),同时256-d不变(如图4和图7中的红框)
- 假设在conv5 feature map中每个点上有k个anchor(默认k=9),而每个anhcor要分前景和背景,所以每个点由256d feature转化为cls=2k scores(二分类嘛);而每个anchor都有(x, y, w, h)对应4个偏移量,所以reg=4k coordinates(回归的四个值)
- 补充一点,全部anchors拿去训练太多了,训练程序会在合适的anchors中随机选取128个postive anchors+128个negative anchors进行训练(后面再说)
注意,在本文讲解中使用的VGG conv5 num_output=512,所以是512d,其他类似。
言归正传,其实RPN最终就是在原图尺度上,设置了密密麻麻的候选Anchor。然后用cnn去判断哪些Anchor是里面有目标的前景,哪些是没目标的背景。所以,仅仅是个二分类而已!
那么Anchor一共有多少个?原图800x600,VGG下采样16倍,feature map每个点设置9个Anchor,所以:
c e i l ( 600 / 16 ) ∗ c e i l ( 800 / 16 ) ∗ 9 = 37 ∗ 50 ∗ 9 = 16650 ceil(600/16) * ceil(800/16) * 9 = 37 * 50 * 9 = 16650 ceil(600/16)∗ceil(800/16)∗9=37∗50∗9=16650
其中ceil()表示向上取整,是因为VGG输出的feature map size= 37*50。
2.2 RPN的真值与预测量
理解RPN的预测量与真值分别是什么,也是理解RPN原理的关键。对于物体检测任务来讲,模型需要预测每一个物体的类别及其出现的位置,即类别、中心点坐标x与y、宽w与高h这5个量。由于有了Anchor这个先验框,RPN可以预测Anchor的类别作为预测边框的类别,并且可以预测真实的边框相对于Anchor的偏移量,而不是直接预测边框的中心点坐标x与y、宽高w与h。
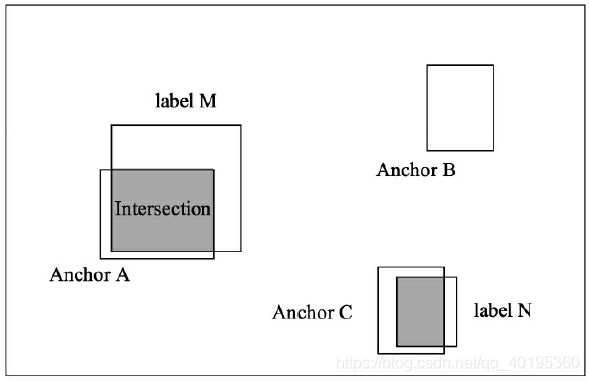
举个例子,如图9所示,输入图像中有3个Anchors与两个标签,从位置来看,Anchor A、C分别和标签M、N有一定的重叠,而Anchor B位置更像是背景。
首先介绍模型的真值。对于类别的真值,由于RPN只负责区域生成,保证recall,而没必要细分每一个区域属于哪一个类别,因此只需要前景与背景两个类别(二分类),前景即有物体,背景则没有物体。
RPN通过计算Anchor与标签的IoU来判断一个Anchor是属于前景还是背景。IoU的含义是两个框的公共部分占所有部分的比例,即重合比例。在图9中,Anchor A与标签M的IoU计算公式如式如下:
IoU ( A , M ) = A ∩ M A ∪ M \operatorname{IoU}(A, M)=\frac{A \cap M}{A \cup M} IoU(A,M)=A∪MA∩M
当IoU大于一定值时,该Anchor的真值为前景,低于一定值时,该Anchor的真值为背景。
然后是偏移量的真值。如图10所示绿色框为飞机的Ground Truth(GT),红色为提取的positive anchors,即便红色的框被分类器识别为飞机,但是由于红色的框定位不准,这张图相当于没有正确的检测出飞机。所以我们希望采用一种方法对红色的框进行微调,使得positive anchors和GT更加接近。
对于窗口一般使用四维向量 ( x , y , w , h x,y,w,h x,y,w,h)表示,分别表示窗口的中心点坐标和宽高。对于图 11,红色的框A代表原始的positive Anchors,绿色的框G代表目标的GT,我们的目标是寻找一种关系,使得输入原始的anchor A经过映射得到一个跟真实窗口G更接近的回归窗口G’,即:
- 给定anchor A = ( A x , A y , A w , A h ) A = (A_x , A_y , A_w , A_h) A=(Ax,Ay,Aw,Ah) 和 G T = ( G x , G y , G w , G h ) GT = (G_x , G_y , G_w , G_h) GT=(Gx,Gy,Gw,Gh)
- 寻找一种变换F,使得: F ( A x , A y , A w , A h ) = ( G x ′ , G y ′ , G w ′ , G h ′ ) ≈ ( G x , G y , G w , G h ) = G T F (A_x , A_y , A_w , A_h) = (G_x' , G_y' , G_w' , G_h') ≈ (G_x , G_y , G_w , G_h) = GT F(Ax,Ay,Aw,Ah)=(Gx′,Gy′,Gw′,Gh′)≈(Gx,Gy,Gw,Gh)=GT
那么经过何种变换F才能从图11中的anchor A变为G’呢? 比较简单的思路就是:
- 先做平移 G x ′ = A w ⋅ d x ( A ) + A x G_x' = A_w · d_x(A) + A_x Gx′=Aw⋅dx(A)+Ax G y ′ = A h ⋅ d y ( A ) + A y G_y' = A_h · d_y(A) + A_y Gy′=Ah⋅dy(A)+Ay
- 再做缩放 G w ′ = A w ⋅ e x p ( d w ( A ) ) G_w' = A_w · exp(d_w(A)) Gw′=Aw⋅exp(dw(A)) G h ′ = A h ⋅ e x p ( d h ( A ) ) G_h' = A_h ·exp (d_h(A)) Gh′=Ah⋅exp(dh(A))
注:
其实我觉得接下来就没必要再细讲了,回归嘛!大家应该都是搞过机器学习的,这里就是用的回归最基本的思想。懂得就直接跳过这一节。
观察上面4个公式发现,需要学习的是 d x ( A ) , d y ( A ) , d w ( A ) , , d h ( A ) d_x(A) , d_y(A) , d_w(A), ,d_h(A) dx(A),dy(A),dw(A),,dh(A) 这四个变换。当输入的anchor A与GT相差较小时,可以认为这种变换是一种线性变换, 那么就可以用线性回归来建模对窗口进行微调(注意,只有当anchors A和GT比较接近时,才能使用线性回归模型,否则就是复杂的非线性问题了)。对应于Faster RCNN原文,平移量( t x , t y t_x, t_y tx,ty)与尺度因子( t w , t h t_w, t_h tw,th)如下:
t x = ( G x − A x ) A w t y = ( G y − A y ) A h t w = ln ( G y − A y ) A w t h = ln ( G y − A y ) A h \begin{aligned} t_{x} &=\frac{\left(G_{x}-A_{x}\right)}{A_{w}} \\ t_{y} &=\frac{\left(G_{y}-A_{y}\right)}{A_{h}} \\ t_{w} &=\frac{\ln \left(G_{y}-A_{y}\right)}{A_{w}} \\ t_{h} &=\frac{\ln \left(G_{y}-A_{y}\right)}{A_{h}} \end{aligned} txtytwth=Aw(Gx−Ax)=Ah(Gy−Ay)=Awln(Gy−Ay)=Ahln(Gy−Ay)
接下来的问题就是如何通过线性回归获得 d x ( A ) , d y ( A ) , d w ( A ) , , d h ( A ) d_x(A) , d_y(A) , d_w(A), ,d_h(A) dx(A),dy(A),dw(A),,dh(A) 了。
2.3 RPN卷积网络
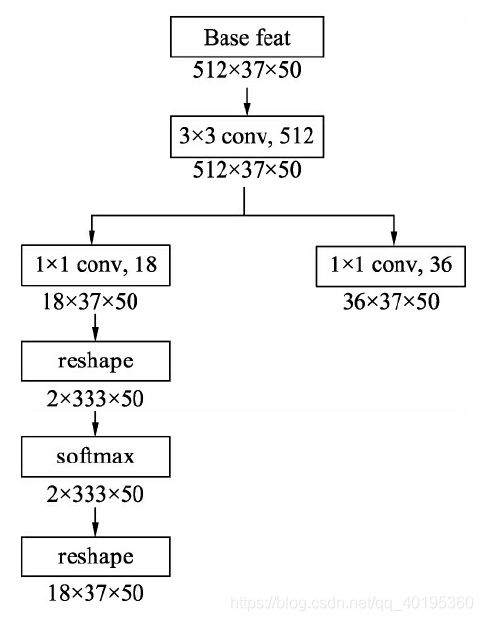
为了实现上述的预测,RPN搭建了如图5、图12所示的网络结构。具体实现时,在feature map上首先用3×3的卷积进行更深的特征提取,然后利用1×1的卷积分别实现分类网络和回归网络。
在物体检测中,通常我们将有物体的位置称为前景,没有物体的位置称为背景。在分类网络分支中,首先使用1×1卷积输出18×37×50的特征,由于每个点默认有9个Anchors,并且每个Anchor只预测其属于前景还是背景,因此通道数为18。随后利用torch.view()函数将特征映射到2×333(9*37)×50,这样第一维仅仅是一个Anchor的前景背景得分,并送到Softmax函数中进行概率计算,得到的特征再变换到18×37×50的维度,最终输出的是每个Anchor属于前景与背景的概率。
在回归分支中,利用1×1卷积输出36×37×50的特征,第一维的36包含9个Anchors的预测,每一个Anchor有4个数据,分别代表了每一个Anchor的中心点横纵坐标及宽高这4个量相对于真值的偏移量。
2.4 RPN真值的求取
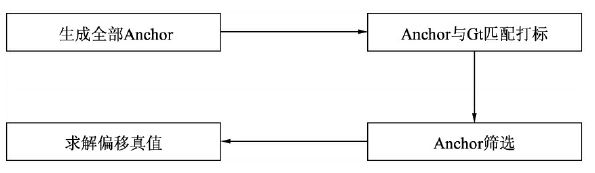
上一节的RPN分类与回归网络得到的是模型的预测值,而为了计算预测的损失,还需要得到分类与偏移预测的真值,具体指的是每一个Anchor是否对应着真实物体,以及每一个Anchor对应物体的真实偏移值。求真值的具体实现过程如图13所示,主要包含4步,下面具体介绍。
1. Anchor生成
这部分与前面Anchor的生成过程一样,可以得到37×50×9=16650个Anchors。由于按照这种方式生成的Anchor会有一些边界在图像边框外,因此还需要把这部分超过图像边框的Anchors过滤掉。
2. Anchor与标签的匹配
为了计算Anchor的损失,在生成Anchor之后,我们还需要得到每个Anchor的类别,由于RPN的作用是建议框生成,而非详细的分类,因此只需要区分正样本与负样本,即每个Anchor是属于正样本还是负样本。前面已经介绍了通过计算Anchor与标签的IoU来判断是正样本还是负样本。在具体实现时,需要计算每一个Anchor与每一个标签的IoU,因此会得到一个IoU矩阵,具体的判断标准如下:
- 对于任何一个Anchor,与所有标签的最大IoU小于0.3,则视为负样本。
- 对于任何一个标签,与其有最大IoU的Anchor视为正样本。
- 对于任何一个Anchor,与所有标签的最大IoU大于0.7,则视为正样本。
需要注意的是,上述三者的顺序不能随意变动,要保证一个Anchor既符合正样本,也符合负样本时,赋予正样本。并且为了保证这一阶段的召回率,允许多个Anchors对应一个标签,而不允许一个标签对应多个Anchors。
3. Anchor的筛选
由于Anchor的总数量接近于2万,并且大部分Anchor的标签都是背景,如果都计算损失的话则正、负样本失去了均衡,不利于网络的收敛。在此,RPN默认选择256个Anchors进行损失的计算,其中最多不超过128个的正样本。如果数量超过了限定值,则进行随机选取。当然,这里的256与128都可以根据实际情况进行调整,而不是固定死的。
4. 求解回归偏移真值
上一步将每个Anchor赋予正样本或者负样本代表了预测类别的真值,而回归部分的偏移量真值还需要利用Anchor与对应的标签求解得到,具体公式见式:
t x = ( G x − A x ) A w t y = ( G y − A y ) A h t w = ln ( G y − A y ) A w t h = ln ( G y − A y ) A h \begin{aligned} t_{x} &=\frac{\left(G_{x}-A_{x}\right)}{A_{w}} \\ t_{y} &=\frac{\left(G_{y}-A_{y}\right)}{A_{h}} \\ t_{w} &=\frac{\ln \left(G_{y}-A_{y}\right)}{A_{w}} \\ t_{h} &=\frac{\ln \left(G_{y}-A_{y}\right)}{A_{h}} \end{aligned} txtytwth=Aw(Gx−Ax)=Ah(Gy−Ay)=Awln(Gy−Ay)=Ahln(Gy−Ay)
得到偏移量的真值后,将其保存在bbox_targets中。与此同时,还需要求解两个权值矩阵bbox_inside_weights和bbox_outside_weights,前者是用来设置正样本回归的权重,正样本设置为1,负样本设置为0,因为负样本对应的是背景,不需要进行回归;后者的作用则是平衡RPN分类损失与回归损失的权重,在此设置为1/256。
2.5 损失函数的计算
有了网络预测值与真值,接下来就可以计算损失了。RPN的损失函数包含分类与回归两部分。
L ( { P i } , { t i } ) = 1 N c l s ∑ i L c l s ( p i , p i ∗ ) + λ 1 N r e g ∑ i P i ∗ L r e g ( t i , t i ∗ ) L\left(\left\{P_{i}\right\},\left\{t_{i}\right\}\right)=\frac{1}{N_{c{l s}}} \sum_{i} L_{c{l s}}\left(p_{i}, p_{i}^{*}\right)+\lambda \frac{1}{N_{r e g}} \sum_{i} P_{i}^{*} L_{r{e g}}\left(t_{i}, t_{i}^{*}\right) L({Pi},{ti})=Ncls1i∑Lcls(pi,pi∗)+λNreg1i∑Pi∗Lreg(ti,ti∗)
Σ i L c l s ( p i , p i ∗ ) Σ_{i} L_{c{l s}}(p_{i}, p_{i}^{*}) ΣiLcls(pi,pi∗)代表了256个筛选出的Anchors的分类损失, P i P_i Pi为每一个Anchor的类别真值, p i ∗ p^*_i pi∗为每一个Anchor的预测类别。由于RPN的作用是选择出Proposal,并不要求细分出是哪一类前景,因此在这一阶段是二分类,使用的是交叉熵损失。值得注意的是,在F.cross_entropy()函数中集成了Softmax的操作,因此应该传入得分,而非经过Softmax之后的预测值。
∑ i P i ∗ L r e g ( t i , t i ∗ ) \sum_{i} P_{i}^{*} L_{reg}\left(t_{i}, t_{i}^{*}\right) ∑iPi∗Lreg(ti,ti∗)代表了回归损失。回归损失使用了 s m o o t h L 1 smooth_{L1} smoothL1函数。
L r e g ( t i , t i ∗ ) = ∑ i ∈ x , y , w , h smooth L 1 ( t i − t i ∗ ) smooth L 1 ( x ) = { 0.5 x 2 if ∣ x ∣ < 1 ∣ x ∣ − 0.5 otherwise \begin{aligned} &L_{r e g}\left(t_{i}, t_{i}^{*}\right)=\sum_{i \in x, y, w, h} \operatorname{smooth}_{L 1}\left(t_{i}-t_{i}^{*}\right)\\ &\text {smooth}_{L 1}(x)=\left\{\begin{array}{ll} 0.5 x^{2} & \text { if }|x|<1 \\ |x|-0.5 & \text { otherwise } \end{array}\right. \end{aligned} Lreg(ti,ti∗)=i∈x,y,w,h∑smoothL1(ti−ti∗)smoothL1(x)={0.5x2∣x∣−0.5 if ∣x∣<1 otherwise
s m o o t h L 1 smooth_{L1} smoothL1函数结合了1阶与2阶损失函数,原因在于,当预测偏移量与真值差距较大时,使用2阶函数时导数太大,模型容易发散而不容易收敛,因此在大于1时采用了导数较小的1阶损失函数。
2.6 NMS与生成Proposal
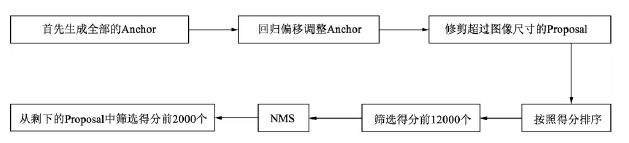
完成了损失的计算,RPN的另一个功能就是区域生成,即生成较好的Proposal,以供下一个阶段进行细分类与回归。NMS生成Proposal的主要过程如图14所示。
Proposal Layer forward 按照以下顺序依次处理:
首先生成大小固定的全部Anchors,然后将网络中得到的回归偏移作用到Anchor上使Anchor更加贴近于真值,并修剪超出图像尺寸的Proposal,得到最初的建议区域。在这之后,按照分类网络输出的得分对Anchor排序,保留前12000个得分高的Anchors。由于一个物体可能会有多个Anchors重叠对应,因此再应用非极大值抑制(NMS)将重叠的框去掉,最后在剩余的Proposal中再次根据RPN的预测得分选择前2000个,作为最终的Proposal,输出到下一个阶段。
2.7 筛选Proposal得到RoI
在训练时,上一步生成的Proposal数量为2000个,其中仍然有很多背景框,真正包含物体的仍占少数,因此完全可以针对Proposal进行再一步筛选,过程与RPN中筛选Anchor的过程类似,利用标签与Proposal构建IoU矩阵,通过与标签的重合程度选出256个正负样本。
这一步有3个作用:
- 筛选出了更贴近真实物体的RoI,使送入到后续网络的物体正、负样本更均衡,避免了负样本过多,正样本过少的情况。
- 减少了送入后续全连接网络的数量,有效减少了计算量。
- 筛选Proposal得到RoI的过程中,由于使用了标签来筛选,因此也为每一个RoI赋予了正、负样本的标签,同时可以在此求得RoI变换到对应标签的偏移量,这样就求得了RCNN部分的真值。
具体实现时,首先计算Proposal与所有的物体标签的IoU矩阵,然后根据IoU矩阵的值来筛选出符合条件的正负样本。
筛选标准如下:
- 对于任何一个Proposal,其与所有标签的最大IoU如果大于等于0.5,则视为正样本。
- 对于任何一个Proposal,其与所有标签的最大IoU如果大于等于0且小于0.5,则视为负样本。
经过上述标准的筛选,选出的正、负样本数量不一,在此设定正、负样本的总数为256个,其中正样本的数量为p个。为了控制正、负样本的比例基本满足1:3,在此正样本数量p不超过64,如果超过了64则从正样本中随机选取64个。剩余的数量256-p为负样本的数量,如果超过了256-p则从负样本中随机选取256-p个。
经过上述操作后,选出了最终的256个RoI,并且每一个RoI都赋予了正样本或者负样本的标签。在此也可以进一步求得每一个RoI的真值,即属于哪一个类别及对应真值物体的偏移量。
3 RoI pooling层
上述步骤得到了256个RoI,以及每一个RoI对应的类别与偏移量真值,为了计算损失,还需要计算每一个RoI的预测量。
前面的VGGNet网络已经提供了整张图像的feature map,因此自然联想到可以利用此feature map,将每一个RoI区域对应的特征提取出来,然后接入一个全连接网络,分别预测其RoI的分类与偏移量。
然而,由于RoI是由各种大小宽高不同的Anchors经过偏移修正、筛选等过程生成的,因此其大小不一且带有浮点数,然而后续相连的全连接网络要求输入特征大小维度固定,这就需要有一个模块,能够把各种维度不同的RoI变换到维度相同的特征,以满足后续全连接网络的要求,于是RoI Pooling就产生了。
对RoI进行池化的思想在SPPNet中就已经出现了,只不过在Fast RCNN中提出的RoI Pooling算法利用最近邻差值算法将池化过程进行了简化,而在随后的Mask RCNN中进一步提出了RoI Align的算法,利用双线性插值,进一步提升了算法精度。
在此我们举一个例子来讲解这几种算法的思想,假设当前RoI大小为332×332,使用VGGNet的全连接层,其所需的特征向量维度为512×7×7,由于目前的特征图通道数为512,Pooling的过程就是如何获得7×7大小区域的特征。
3.1 RoI Pooling简介
RoI Pooling的实现过程如图15所示,假设当前的RoI为图4.9中左侧图像的边框,大小为332×332,为了得到这个RoI的特征图,首先需要将该区域映射到全图的特征图上,由于下采样率为16,因此该区域在特征图上的坐标直接除以16并取整,而对应的大小为332/16=20.75。在此,RoI Pooling的做法是直接将浮点数量化为整数,取整为20×20,也就得到了该RoI的特征,即图15中第3步的边框。
下一步还要将该20×20区域处理为7×7的特征,然而20/7≈2.857,再次出现浮点数,RoI Pooling的做法是再次量化取整,将2.857取整为2,然后以2为步长从左上角开始选取出7×7的区域,这样每个小方格在特征图上都对应2×2的大小,如上图中第4步所示。
最后,取每个小方格内的最大特征值,作为这个小方格的输出,最终实现了7×7的输出,也完成了池化的过程,如图中第5步所示。
从实现过程中可以看到,RoI本来对应于20.75×20.75的特征图区域,最后只取了14×14的区域,因此RoI Pooling算法虽然简单,但量化取整带来的偏差势必会影响网络,尤其是回归物体位置的准确率。
3.2 RoI Align简介
RoI Align的思想是使用双线性插值获得坐标为浮点数的点的值,主要过程如下图所示,依然将RoI对应到特征图上,但坐标与大小都保留着浮点数,大小为20.75×20.75,不做量化。
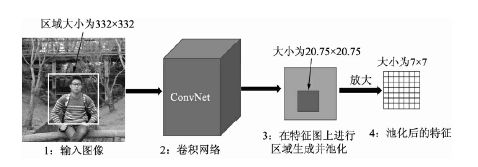
接下来,将特征图上的20.75×20.75大小均匀分成7×7方格的大小,中间的点依然保留浮点数。在此选择其中2×2方格为例,如下图所示,在每一个小方格内的特定位置选取4个采样点进行特征采样,如图中每个小方格选择了4个小黑点,然后对这4个黑点的值选择最大值,作为这个方格最终的特征。这4个小黑点的位置与值该如何计算呢?
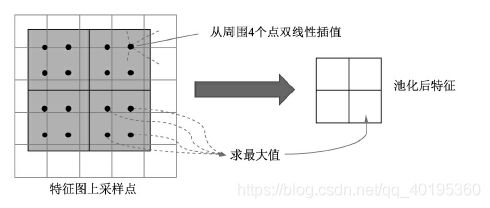
对于黑点的位置,可以将小方格平均分成2×2的4份,然后这4份更小单元的中心点可以作为小黑点的位置。
至于如何计算这4个小黑点的值,RoI Align使用了双线性插值的方法。小黑点周围会有特征图上的4个特征点,利用这4个特征点双线性插
值出该黑点的值。
由于Align算法最大可能地保留了原始区域的特征,因此Align算法对检测性能有显著的提升,尤其是对于受RoI Pooling影响大的情形,如
本身特征区域较小的小物体,改善更为明显。
4 全连接RCNN模块
在经过RoI Pooling层之后,特征被池化到了固定的维度,因此接下来可以利用全连接网络进行分类与回归预测量的计算。在训练阶段,最后需要计算预测量与真值的损失并反传优化,而在前向测试阶段,可以直接将预测量加到RoI上,并输出预测量。
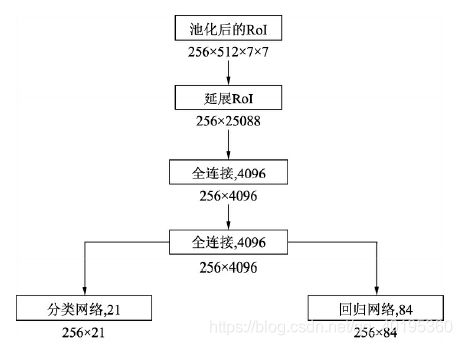
接下来利用VGGNet的两个全连接层,得到长度为4096的256个RoI特征。为了输出类别与回归的预测,将上述特征分别接入分类与回归的全连接网络。在此默认为21类物体,因此分类网络输出维度为21,回归网络则输出每一个类别下的4个位置偏移量,因此输出维度为84。
RCNN部分的损失函数计算方法与RPN部分相同,不再重复。只不过在此为21个类别的分类,而RPN部分则是二分类,需要注意回归时至多有64个正样本参与回归计算,负样本不参与回归计算。