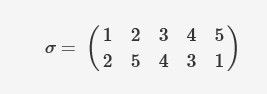独角兽与数列（置换群循环）- HDU 4985

群论是法国数学家伽罗瓦（Galois）的发明。伽罗瓦是一个极具传奇性的人物，年仅21岁就英年早逝于一场近乎自杀的决斗中。他用该理论，具体来说是伽罗瓦群，解决了五次方程问题。在此之前柯西（Augustin-Louis Cauchy)，阿贝尔（Niels Henrik Abel）等人也对群论作出了贡献。

 

群是 集合G+运算符·，它结合任何两个元素a和b而形成另一个元素，记为a·b。符号"·"是对具体给出的运算，比如整数加法的一般占位符。要具备成为群的资格，这个集合和运算( G , · )必须满足叫做群公理的四个要求：

 

1. 封闭性： 对于所有G中a, b，运算a·b的结果也在G中。

 

2. 结合性： 对于所有G中的a, b和c，等式 (a·b)·c = a· (b·c)成立。

 

3. 单位元： 存在G中的一个元素e，使得对于所有G中的元素a，等式e·a = a·e = a成立。

 

4. 逆元： 对于每个G中的a，存在G中的一个元素b使得a·b = b·a = e，这里的e是单位元。

 

 

置换：

一个有限集X的置换σ是从该有限集映至自身的双射，如果我们把G的元素从1到|X|编号，那么置换σ可以看做一个1到|X|的一个排列，其中第i个位置上的数设为ai，表示编号为i的元素变为编号为ai的元素。

记为

 

循环：

本题中，对于σ排列，还存在一个循环分组，循环分组的逻辑是：

对于排列(2 5 4 3 1)，从a[1]开始，查找a[a[1]]的值，如下题中的图，也就是查找a[2]的值，接着查找a[a[2]]的值，也就是a[5]，接着查找a[a[5]]的值，也就是a[1]，正好形成一个循环。对于a[3]，接着查找a[a[3]]，也就是a[4]，对于a[a[4]]，也就是a[3]，形成另外一个循环。

 

群论的概念比较新颖，要熟练运用还有很多路要走，这里只能略讲皮毛，有个大概的了解~

 

 

Problem Description

As a unicorn, the ability of using magic is the distinguishing feature among other kind of pony. Being familiar with composition and decomposition is the fundamental course for a young unicorn. Twilight Sparkle is interested in the decomposition of permutations. A permutation of a set S = {1, 2, ..., n} is a bijection from S to itself. In the great magician —— Cauchy's two-line notation, one lists the elements of set S in the first row, and then for each element, writes its image under the permutation below it in the second row. For instance, a permutation of set {1, 2, 3, 4, 5} σ can be written as: 

作为一只独角兽，使用魔法是唯一能够区别于小马的特征。小独角兽的基础课程是熟悉组合与拆解。TS独角兽对数列的拆解非常感兴趣。集合S的一个排列是S的一个双向映射。柯西的两行标记魔法中，一行列出S的元素，然后对于每个元素，写出该元素的映射，放置于第二行中。比如集合{1,2,3,4,5}的排列σ可以写作：

 

Here σ(1) = 2, σ(2) = 5, σ(3) = 4, σ(4) = 3, and σ(5) = 1. 

 

Twilight Sparkle is going to decompose the permutation into some disjoint cycles. For instance, the above permutation can be rewritten as: 

TS准备拆解这个组合成一些不相连的循环组，比如，上面的排列可以这样写：

 

Help Twilight Sparkle find the  lexicographic smallest solution. (Only considering numbers).

帮助TS寻找字典序列的最小值。

 

Input

Input contains multiple test cases (less than 10). For each test case, the first line contains one number n (1<=n<=10^5). The second line contains n numbers which the i-th of them(start from 1) is σ(i).

多个测试用例，对于每个测试用例，第一行是一个整数n。第二行包含n个数表示序列的每个数字。

 

Output

For each case, output the corresponding result.

 

Sample Input

5 
2 5 4 3 1 
3
1 2 3

Sample Output

(1 2 5)(3 4) 
(1)(2)(3)

源代码：G++

#include 
#include 

int main()
{
    int n;
    //小于10的5次方
    int values[100017], flags[100017];

    while (~scanf("%d", &n))
    {
        //
        memset(flags, 0, sizeof(flags));
        //依次输入组合
        for (int i = 1; i <= n; i++)
        {
            scanf("%d", &values[i]);
        }

        //寻找所有环状数列
        for (int i = 1; i <= n; i++)
        {
            //如果f[i]有值了，说明已经在某个环状集合里面了，继续寻找没有处理的元素
            if (flags[i])
                continue;

            //标记第一个数
            int j = i;
            flags[j] = 1;
            printf("(%d", j);
            //寻找环状数列
            while (flags[values[j]] == 0)
            {
                printf(" %d", values[j]);
                //标记以寻找
                flags[values[j]] = 1;
                //寻找下一个
                j = values[j];
            }
            printf(")");
        }
        printf("\n");
    }

    return 0;
}

个人公众号：ACM算法日常

专注于基础算法的研究工作，深入解析ACM算法题，五分钟阅读，轻松理解每一行源代码。内容涉及算法、C/C++、机器学习等。