【Trie树&分治&异或】2020牛客暑期多校训练营（第五场）B - Graph

问题：Graph

问题传送门

题目大意：

给你一个具有 $n$ 个节点，$n-1$ 条边的无环图，也可称其为树。你可以执行两种操作，在图中加一条边或删掉一条边，你可以执行任意多次，在整个操作过程中，要保证整个图是连通的，如果出现环的话，要保证整个环上的所有边的异或和为0；求最小异或生成树（其实也可以直接说成是求最小生成树，只不过，在此边权是两个顶点点权的异或值而已）。

解题思路：

写这个题的时候，完全就可以和另外一道题类比起来进行考虑；
题目链接：Codeforce G. Xor-MST
题解：G. Xor-MST

两题进行对比
（1）来再次简单回忆一下 $cf$ 的这道题,给你的是 $n$ 个点的的点权，任意两点之间的连边的边权等于两个顶点点权的异或值。所以就可以知道任意两点连边的边权，当然，此为完全图。
（2）本题的话，也可以先构造这个图的完全图，然后根据最小生成树算法来求解，但是数据范围不太允许，必定超时，因此也是和cf的这道题的做法一样，利用 $trie$ 树来进行优化,最后用分治的思想求解最小生成树。

为什么说这两题有联系呢，因为在构建这个图的完全图时，正好是和 $cf$ 的那个道题是一致的,要满足任意一个环内的异或值为零，则新加进去的那个边权为其他所有边的异或和。

利用边权来求的话不太好求，利用边权求最小生成树的算法 $prim$ 和 $kruskal$ 算法。完全图边的数量有$（n-1{）}^2$ 条，$n$ 的范围 $1e5$ ,时间复杂度不允许这样来。
想到 $cf$ 的那道题给定的是所有点的点权，且满足两个点点权的异或值等于边权这一性质；
本题也构造出这样的点权，任意两点点权的异或值等于这两个点连边的边权，恰好也能满足题目中第二个要求，一个环内的所有边的异或和为 $0$.

接下来就转化成求每个点的点权，每个点的点权求出后按照和 $cf$ 那道题同样的解法就能解决此题。

可利用 $dfs$ 来求取一棵树中每个点的点权此处可直接认为每个点的点权即为每个点到根节点上所有边的异或值。
接下来放上两个 $dfs$ 代码

/*递归求一棵树上每个节点到根节点的距离*/
void dfs(int u,int fa){
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa) continue;
        dist[j]=dist[u]+w[i];
        dfs(j,u);
    }
}

/*递归求一棵树上是任意一点到根节点边的异或和*/
void dfs(int u,int fa)
{
	for(int i = h[u];i != -1;i = ne[i])
	{
		int j = e[i];
		if(j == fa) continue;
		val[j] = val[u] ^ (1ll * w[i]);
		dfs(j,u);
	}
}

是不是发现极为神似，没错，树上求距离就是这么简单，更复杂一点利用 $dijkstra$ 也是可以解决的,想当初做的那道线上倍增法求LCA就这么干过，这里就不细说了（手动滑稽。。。）
来看一下，样例$dfs$后的结果吧，红色数字代表的是每个点的点权。

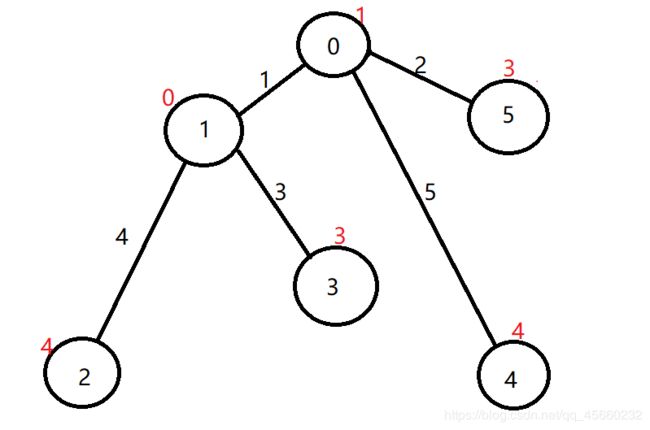
可以手动求一下，任意两点的连边，一定是满足题目要求的。

还有其他的操作，和 $cf$ 的那道题是一样的，就不再细述了，可直接转至博客查看

上代码：

#include
using namespace std;
typedef long long ll;
const int M = 6000010;
const int N = 200010;
int son[M][2],idx;
int h[N],e[2*N],w[2*N],ne[2*N],cnt;
ll val[M];
int L[M],R[M];
void add(int a,int b,int c)
{
	e[cnt] = b; w[cnt] = c; ne[cnt] = h[a];h[a] = cnt++; 
}
void dfs(int u,int fa)
{
	for(int i = h[u];i != -1;i = ne[i])
	{
		int j = e[i];
		if(j == fa) continue;
		val[j] = val[u] ^ (1ll * w[i]);
		dfs(j,u);
	}
}
void insert(ll x,int id)
{
	int p = 0;
	for(int i = 31;i >= 0;i--)
	{
		int s = x >> i & 1ll;
		if(!son[p][s]) son[p][s] = ++idx;
		p = son[p][s];
		if(L[p] == -1) L[p] = id;//细节
		R[p] = id;
	}
}
ll query(int p,int pos,ll x)
{
	ll res = 0;
	for(int i = pos;i >= 0;i--)
	{
		int s = x >> i & 1ll;
		if(son[p][s]) p = son[p][s];
		else{
			res += 1ll << i;
			p = son[p][!s];
		}
	}
	return res;
}
ll divide(int p,int pos)
{
	if(son[p][0] && son[p][1])
	{
		int x = son[p][0],y = son[p][1];
		ll min1 = 0x3f3f3f3f;
		for(int i = L[x];i <= R[x];i++) min1 = min(min1,query(y,pos - 1,val[i]) + (1ll << pos));
		return min1 + divide(son[p][0],pos - 1) + divide(son[p][1],pos - 1);
	}
	else if(son[p][0]) return divide(son[p][0],pos - 1);
	else if(son[p][1]) return divide(son[p][1],pos - 1);
	return 0;
}
int main()
{
	int n;
	scanf("%d",&n);
	memset(h,-1,sizeof h);
	memset(L,-1,sizeof L);//细节
	memset(R,-1,sizeof R);
	for(int i = 1;i <= n - 1;i++)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
//		x++,y++;
		add(x,y,z);
		add(y,x,z);
	}
	dfs(1,-1);
	sort(val,val + n);
	//for(int i = 1;i <= n;i++) cout<
	for(int i = 0;i < n;i++) insert(val[i],i);
	printf("%lld\n",divide(0,31));
	return 0;
 } 

有必要注意的细节：这份代码展示的是点的下标是从 $0$ 开始的，在代码中就需要注意细节问题了，可翻看代码中注释有细节的那些位置。当然从 $1$ 开始会简便一点，至少不需要初始化 $L$ 和 $R$ 数组了。

特别鸣谢：光光学长帮我解疑，渣渣松同学与我一块儿讨论。

另外此题他们都写有博客，我在此也推一下。

光光学长的题解
渣渣松同学的题解

完结。