笔记︱决策树族——梯度提升树(GBDT）

 

每每以为攀得众山小，可、每每又切实来到起点，大牛们，缓缓脚步来俺笔记葩分享一下吧，please~

———————————————————————————

 

本笔记来源于CDA DSC，L2-R语言课程所学进行的总结。

 

 

 

一、介绍：梯度提升树（Gradient Boost Decision Tree）

Boosting算法和树模型的结合。按次序建立多棵树，每棵树都是为了减少上一次的残差(residual)，每个新的模型的建立都是为了使之前模型的残差往梯度方向减少。最后将当前得到的决策树与之前的那些决策树合并起来进行预测。

相比随机森林有更多的参数需要调整。

 

————————————————————————————————————————————————————————————

 

 

二、随机森林与梯度提升树（GBDT）区别

 

随机森林：决策树+bagging=随机森林

梯度提升树：决策树Boosting=GBDT

两者区别在于bagging boosting之间的区别，可见:

 

	bagging	boosting
取样方式	bagging采用均匀取样	boosting根据错误率来采样
精度、准确性	相比之，较低	高
训练集选择	随机的，各轮训练集之前互相独立	各轮训练集的选择与前面各轮的学习结果相关
预测函数权重	各个预测函数没有权重	boost有权重
函数生成顺序	并行生成	顺序生成
应用	象神经网络这样极为消耗时间的算法，bagging可通过并行节省大量的时间开销 baging和boosting都可以有效地提高分类的准确性	baging和boosting都可以有效地提高分类的准确性 一些模型中会造成模型的退化（过拟合） boosting思想的一种改进型adaboost方法在邮件过滤，文本分类中有很好的性能
	随机森林	梯度提升树

 

GDBT为什么受到比赛圈、工业界的青睐：

GBDT 它的非線性變換比較多，表達能力強，而且不需要做複雜的特徵工程和特徵變換。

GBDT的優勢 首先得益於 Decision Tree 本身的一些良好特性，具體可以列舉如下:

1. Decision Tree 可以很好的處理 missing feature，這是他的天然特性，因為決策樹的每個節點只依賴一個 feature，如果某個 feature 不存在，這顆樹依然可以拿來做決策，只是少一些路徑。像邏輯迴歸，SVM 就沒這個好處。

2. Decision Tree 可以很好的處理各種類型的 feature，也是天然特性，很好理解，同樣邏輯迴歸和 SVM 沒這樣的天然特性。

3. 對特徵空間的 outlier 有魯棒性，因為每個節點都是 x < ? 的形式，至於大多少，小多少沒有區別，outlier 不會有什麼大的影響，同樣邏輯迴歸和 SVM 沒有這樣的天然特性。

4. 如果有不相關的 feature，沒什麼干擾，如果數據中有不相關的 feature，頂多這個 feature 不出現在樹的節點裏。邏輯迴歸和 SVM 沒有這樣的天然特性(但是有相應的補救措施，比如邏輯迴歸裏的 L1 正則化)。

5. 數據規模影響不大，因為我們對弱分類器的要求不高，作為弱分類器的決策樹的深 度一般設的比較小，即使是大數據量，也可以方便處理。像 SVM 這種數據規模大的時候訓練會比較麻煩。 

當然 Decision Tree 也不是毫無缺陷，通常在給定的不帶噪音的問題上，他能達到的最佳分類效果還是不如 SVM，邏輯迴歸之類的。但是，我們實際面對的問題中，往往有很大的噪音，使得 Decision Tree 這個弱勢就不那麼明顯了。而且，GBDT 通過不斷的疊加組合多個小的 Decision Tree，他在不帶噪音的問題上也能達到很好的分類效果。換句話説，通過GBDT訓練組合多個小的 Decision Tree 往往要比一次性訓練一個很大的 Decision Tree 的效果好很多。因此不能把 GBDT 理解為一顆大的決策樹，幾顆小樹經過疊加後就不再是顆大樹了，它比一顆大樹更強。  

来源：梯度提升決策樹（GBDT）與XGBoost、LightGBM

 

—————————————————————————————————————————————————————

 

 

三、R中与决策树有关的Package

单棵决策树：rpart/tree/C50
随机森林：randomforest/ranger
梯度提升树：gbm/xgboost
树的可视化：rpart.plot

 

————————————————————————————————————

 

延伸：GDBT的局部+ 全局解释性

来自支付宝论文：深度 | 蚂蚁金服DASFAA论文带你深入了解GBDT模型

GDBT模型的解释一般来说分为全局解释性 / 局部解释性。其特点为：

第一，GBDT这种树形模型的权值存在于叶子结点上，一个叶子结点实际上是从根节点开始，由一系列特征分裂点、特征分裂值决定的一条路径，也就是一个叶节点上的分值是多个特征共同决定的；

第二，由于GBDT模型的特点，它的每一棵树拟合的都是当前的残差，同一特征在不同的树上贡献度也是不同的，因为随着残差的逐渐减小，后面的树对最后预测分值的贡献度也是更小的，因此随机森林RF（Random Forest）模型那种基于样本标签分布变化的局部解释性方案不适用于GBDT模型。

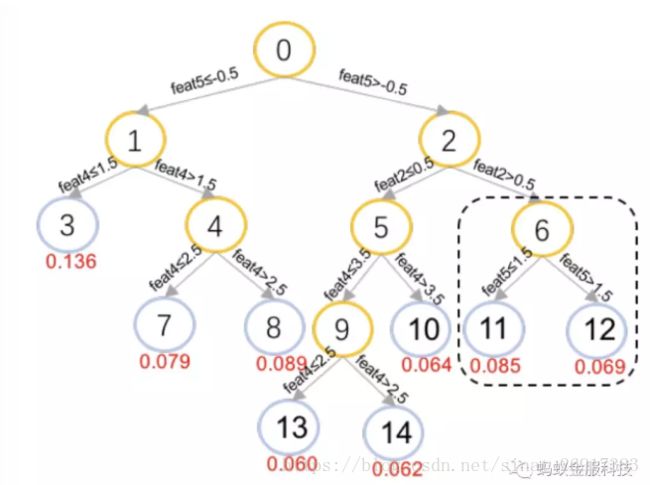
GBDT的模型可以使用PMML (Predictive Model Markup Language)的格式来记录，如图：

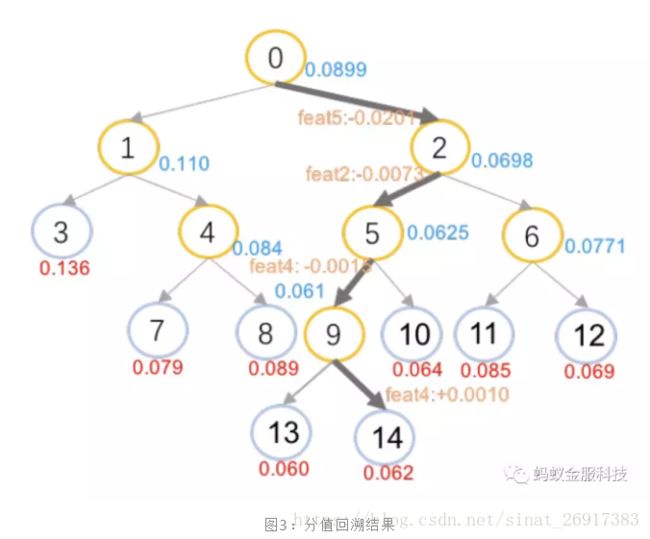
观察图2中的节点6、节点11和节点12，由父节点6向两个子节点前进的过程中，会对特征feat5进行判断，若其小于等于1.5则落向节点11获得0.085的预测分，否则落向节点12获得0.069的预测分。也就是在这一步的前进当中，由于特征feat5的不同，一个样本可能会获得的分值差异为Sn11 − Sn12 = 0.085 – 0.069 = 0.016，Snk表示在节点k上的得分。所以，可以通过求两个叶节点的平均值获得对节点6的分值估计，再通过自底向上回溯的方式，可以将分数回溯到所有中间节点最后到达根节点。

这样就实现了局部特征贡献度的定义，将分数分摊到各个特征上，图2示例的处理结果标识在图3当中。蓝色的分值表示中间节点获得的分值估计，边上的橙色部分表示了经过该条边时的贡献特征和贡献分值。

我们使用阿里内部基于参数服务器的GBDT分布式版本SMART(Scalable Multiple Additive Regression Tree)进行模型的训练，并记录样本在节点上的分布情况。

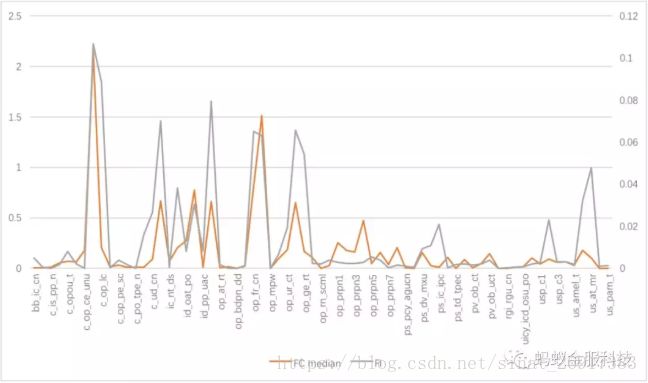
局部模型解释方案是对单条样本进行的，我们对大量样本输出的解释观察时，对于每一维特征存在一个贡献度的分布，我们取这个分布的中位数作为其一般衡量，它应该与全局模型解释对各个特征重要性大小的判断保持一致，分析结果如图4所示，橙色、灰色分别表示各个特征的局部、全局解释，具有我们预估的一致性，说明本文GBDT的局部解释方案较为可靠。

我们还通过人工进行具体解释案例检查，分析支付宝交易测试集，发现本文模型解释输出的高风险特征与人工判断一致，并且还能抓出一些全局重要性不高，但在特定样本中属于高风险的特征，验证了结果的可靠性和实用性。

模型解释还可以用于模型检查，通过给数据分析师一个直观解释，判断与人工归因的一致性来验证模型的效果，从而使他们相信机器学习模型。另一方面，模型解释也可以用于模型的提高，通过对漏抓、误抓样本的解释，可以对特征进行补充、修改，进而实现模型的更新迭代和效果的进一步提升。

 

每每以为攀得众山小，可、每每又切实来到起点，大牛们，缓缓脚步来俺笔记葩分享一下吧，please~

———————————————————————————