【图像处理】射线爆发算法(Rayburst algorithm)
【fishing-pan:https://blog.csdn.net/u013921430 转载请注明出处】
射线爆发方法简介
射线爆发算法(Rayburst algorithm)是一种经常被用于分析平面或者3D空间中复杂、不规则结构的算法。算法的核心思想很简单,如它的名字所描述的一样:以某一点为中心,向周围爆发出多条射线,射线的起点始就是中心点,这些射线分别沿着各自的方向延伸,直到达到终止条件。我们可以将这个过程想象成在一个灯泡向周围投射出光线的过程。最终通过这些射线的长度信息,我们可以得到结构的尺寸,形状等信息。

射线爆发算法中最主要的步骤有两个:生成采样核(Generating sampling core)和投射射线(Casting rays)。生成采样核通俗来讲就是得到初始化的射线方向,而投射射线就是上一段中所描述的射线沿着各自的方法延伸的过程。3D空间内的射线爆发方法比二维平面的更加复杂,所以我们接下来主要介绍3D空间的射线爆发方法。
生成采样核
生成采样核是射线爆发算法中最关键的一步。为了尽量使射线爆发方法所得到的物体形态与真实形态接近,应该得到尽量多的射线方向,并且尽量使射线方向分布均匀。在3D空间中,当所需要描述的物体的体积比较小或者是形态比较规则时,可以直接用中心点的26邻域的方向作为采样核。而若想生成包含更多方向的采样核,则往往需要借助于单位球。接下来将详细介绍三种采样核生成方法。
基于角度等分的采样核生成方法
我们可以用角度等分的方法得到一系列的射线方向,但是在直角坐标系中,我们很难对角度进行描述。因此,可以将坐标系转换成球坐标系。
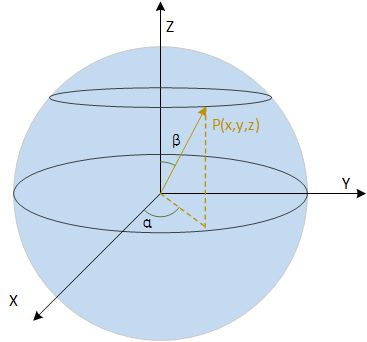
生成采样核的过程其实就是得到单位球球面上的一系列点的坐标的过程,例如上图中球面上的一点 p p p,它的坐标可以由方位角 α α α 和仰角 β β β 得到,具体可以表示为以下公式。
{ x = c o s α s i n β y = s i n α s i n β z = c o s β \left\{\begin{matrix} x=&cos\alpha sin\beta \\ y=&sin\alpha sin\beta \\ z=&cos\beta \end{matrix}\right.\\ ⎩⎨⎧x=y=z=cosαsinβsinαsinβcosβ
通过对方位角和仰角进行等分,可以得到一系列的球面上的点。其中 α α α 和 β β β 的取值如下;
{ α ⊆ [ 0 , 2 π ) β ⊆ [ 0 , π ] \left\{\begin{matrix} \alpha \subseteq &\left [ 0, 2\pi \right )\\ \beta \subseteq &\left [ 0 , \pi \right ] \end{matrix}\right. {α⊆β⊆[0,2π)[0,π]
之所以β的取值能够取到 π π π ,是因为 Z Z Z 轴正负方向是不同的。如果将方位角分成 m m m 等分,仰角进行 n n n 等分,理论上将得到 m ∗ ( n + 1 ) m*(n+1) m∗(n+1) 个方向,但是当仰角为 0 0 0 或者 π \pi π 时,不会生成 m m m 个方向,而是只有一个方向,所以最终只会生成 m ∗ ( n + 1 ) − 2 ∗ ( m − 1 ) m*(n+1)-2*(m-1) m∗(n+1)−2∗(m−1) 个方向。下图是 m = 14 m=14 m=14、 n = 7 n=7 n=7 时候所生成的采样核,其中包含86个方向。
基于多面体的采样核生成方法
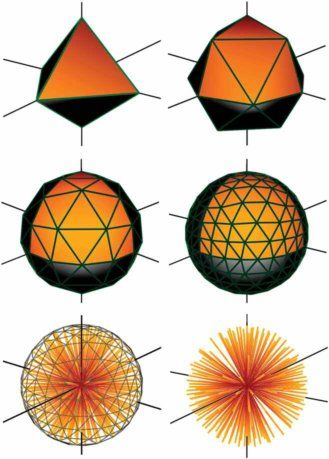
借助于内接于单位球的多面体,也可以生成采样核。步骤示意图如下图所示,图中多面体的顶点坐标就是采样核中的射线方向。
- 生成内接于球的正八面体。为了简化模型,实际过程中,可以将八面体的六个顶点设在坐标轴上;
- 将每一个面划分成4个小三角形,并且通过归一化使每一个新生成的顶点内接于球面。
- 重复第二步,直到生成了足够的顶点。最终球心到顶点的方法就是射线方向。
从上述过程可以看出,最初的八面体有6个顶点,第一次迭代得到的32面体有18个顶点,第二次迭代得到的96面体有66个顶点,第三次迭代的386面体有258个顶点。设迭代次数为n,通过等比数列求和可知,进过 n n n 次迭代,最终得到的顶点数为 4 n + 1 + 2 4^{n+1}+2 4n+1+2 个。通过该方法,本文得到了 n = 0 , 1 , 2 , 3 n=0,1,2,3 n=0,1,2,3 时的四个采样核,如下图所示。

使用该方法得到的采样核进行射线爆发操作,还可以估算物体的表面积和体积。如下图中所示。通过计算每一个三角形的面积,最终可以得到物体的表面积,而通过计算每一个四面体的体积,可以近似得到物体的体积。
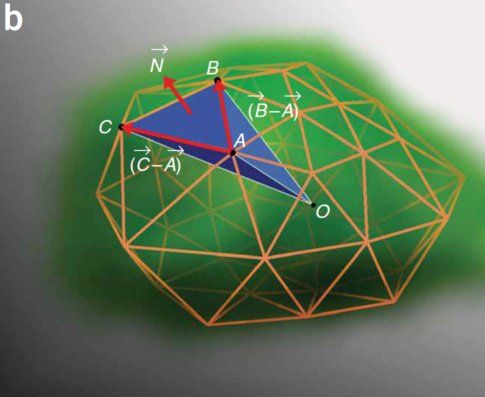
详细的计算公式如下;
N i ⃗ = 0.5 ∗ ( B i ⃗ − A i ⃗ ) × ( C i ⃗ − A i ⃗ ) \vec{N_{i}}=0.5*\left ( \vec{B_{i}}-\vec{A_{i}} \right )\times \left (\vec{C_{i}}-\vec{A_{i}} \right ) Ni=0.5∗(Bi−Ai)×(Ci−Ai)
S A i = 0.5 ∗ ∥ N i ⃗ ∥ SA_{i}=0.5*\left \| \vec{N_{i}} \right \| SAi=0.5∗∥∥∥Ni∥∥∥
V i = 1 3 S A i ∣ N i ⃗ ⋅ ( A i ⃗ − O ⃗ ) ∥ N i ⃗ ∥ ∣ = 1 6 ∥ N i ⃗ ⋅ ( A i ⃗ − O ⃗ ) ∥ \begin{aligned} V_{i}&=\frac{1}{3}SA_{i}\left | \frac{\vec{N_{i}}\cdot (\vec{A_{i}}-\vec{O})}{\left \| \vec{N_{i}} \right \|} \right | \\ &=\frac{1}{6}\left \|\vec{N_{i}}\cdot(\vec{A_{i}}-\vec{O}) \right \| \end{aligned} Vi=31SAi∣∣∣∣∣∣∥∥∥Ni∥∥∥Ni⋅(Ai−O)∣∣∣∣∣∣=61∥∥∥Ni⋅(Ai−O)∥∥∥
通过以上公式,我们计算了单位球内采样核所构成的多面体的表面积。
| 采样核数目 | 6 | 18 | 66 | 258 | 球体 |
|---|---|---|---|---|---|
| 表面积 | 6.92820311 | 10.4177513 | 11.9549055 | 12.4081726 | 12.5663706 |
从表格中可以看出,当采样核所包含的方向越多,所构成的多面体的表面积与球体表面积越接近,所以一般情况系,采样核所包含的方向越多,所得到的最终结果越接近真实的物体形态。
基于随机数&能量最小化的采样核生成方法
从上面描述中可以看出,这两种方法得到的采样核所包含的方向的数目是难以变动的,尤其是基于多面体的方法。当我们希望生成任意数量方向的采样核时,可以使用随机数&能量最小的方法。该方法的思路也很简单;
- 在单位球上随机生成 n n n 个点;
- 对于单个点,其余的 n − 1 n-1 n−1 个点都对它有排斥力,力的大小与两点之间的球面距有关,球面距越大排斥力越小。 某个点所受到的排斥力的合力驱使该点沿着力的方向移动。所有点受到的排斥力的和称为系统的能量 E E E。对所有的点依次进行一次移动的过程称为一次迭代。
- 不断地进行迭代,当前后两次迭代的能量 E E E 的变化小于某一值时,认为系统达到稳定,停止迭代。
投射射线
在得到采样核后,对于采样核中的每个射线方向,分别沿着方向进行搜索。当达到终止条件时,射线停止延伸。在实际应用中,终止条件一般是信号强度阈值或者梯度阈值。
由于采样核中的方向是单位向量,这些向量在坐标轴上的分量大都不是整数,而搜索的步长却往往是整数,因此搜索过程中经常无法整数的坐标位置。在这种情况下,直接取整的做法很容易损失精度,所以,在实际计算过程中,一般会使用插值进行计算。例如在三维空间中,可以使用三线性插值得到搜索路径上的信号强度。
最后
除了上述问题外,起始中心点的位置对于射线爆发方法计算结果也存在着巨大的影响。选取不同的爆发起始点,计算结果往往不同,尤其是在物体极度不规则的情况下。人们一般会使用人工标注或者使用距离变换的方法来确定爆发起始点。
代码
在这里我贴出基于角度等分的采样核生成方法的代码,希望对大家有所帮助。我也会把这些采样核放在网上,大家有需要的可以点击这里,自行下载。
//------------------------------------------
//作者:不用先生,2019.04.28
//函数名:generatingSamplingCore
//函数功能:采用球坐标的方法生成射线爆发所需的采样核,即射线方向向量;
//参数:int m:表示在方位角内,分成m个方向;
//参数:int n:表示在仰角内有n+1个方向,因为-1与1是两个不同的方向;
//最终生成的向量数目为m*(n+1)-2*(m-1)
//参数 vector> &vec:vec用于记录方向向量,vec中的每一个vector是一个方向,相邻的两个方向互为反向量;
bool generatingSamplingCore(int m, int n, vector<vector<float>> &vec)
{
float min_value = 0.0001;
for (int i = 0; i <= n/2; i++) //注:循环内只生成仰角小于等于90度的方向,其他关于XY平面镜像对称的方向可以取反得到;
{
for (int j = 0; j < m; j++)
{
float alpha = float(j) * 2 * PI / float(m);
float beta = float(i) * PI / float(n);
float x = sin(beta)*cos(alpha); if (abs(x) < min_value){ x = 0; } //因为PI不够精确,可能存在一些方向存在很小的误差,强制矫正;
if (1 - abs(x) < min_value)
{
if (x < 0)
{
x = -1;
}
else
{
x = 1;
}
}
float y = sin(beta)*sin(alpha); if (abs(y) < min_value){ y = 0; }
if (1 - abs(y) < min_value)
{
if (y < 0)
{
y = -1;
}
else
{
y = 1;
}
}
float z = cos(beta); if (abs(z) < min_value){ z = 0; }
if (1 - abs(z) < min_value)
{
if (z < 0)
{
z = -1;
}
else
{
z = 1;
}
}
//-------------保存方向向量何其反向量;
vector<float> sub_vec;
sub_vec.push_back(x);
sub_vec.push_back(y);
sub_vec.push_back(z);
vec.push_back(sub_vec);
sub_vec.clear();
if (z != 0) //当z=0时,仰角为90度,此时方向的反方向,在XY平面内,如果取反,会重复得到这一向量。
{
sub_vec.push_back(-x);
sub_vec.push_back(-y);
sub_vec.push_back(-z);
vec.push_back(sub_vec);
}
if (abs(z) == 1) //当方向为0,0,1和0,0,-1时,不需要进行方向角的循环了!
{
break;
}
}
}
return true;
}
参考文献
Rodriguez A , Ehlenberger D B , Hof P R , et al. Rayburst sampling, an algorithm for automated three-dimensional shape analysis from laser scanning microscopy images[J]. NATURE PROTOCOLS, 2006, 1(4):2152-2161.
。。。已完