集成学习

简介

并不是所有的集成学习框架中的基学习器都是弱模型。
弱模型是偏差高(在训练集上准确度低)方差小(防止过拟合能力强)的模型。常指泛化性能略优于随机猜测的学习器，例如在二分类问题上精度略高于50%的分类器。其分类性能并不是很强。
目前常用的三种框架是Bagging、Boosting和Stacking。
Boosting 是弱模型，偏差高方差低
Bagging 和Stacking是强模型，偏差低方差高

Bagging

并行算法，个体学习器间存在强依赖关系

1. 随机从样本中有放回得抽样，抽得n个样本，做为一个训练集(Boostraping方法)。 重复k次，得到k个训练集(每一轮都独立采样)。
2. k个训练集共得到k个基模型。
3. 最终结果
   各模型权重相同，
   对分类问题：采用多数投票方式。
   对回归问题：采用加和取均值方式。

Boosting

串行算法，个体学习器间存在强依赖关系

1. 每个基学习器中有个系数 代表其权重 即该基学习器的价值，分类误差小的分类器权值大
2. 后一个分类器学习前一个的残差，将前一个中的判断正确的权重降低，判断错误的升高。达到不断修正的效果，后一个模型是对前一个的加强。当残差足够小或达到设置的最大迭代次数则停止。
3. 使用代价函数对上一轮训练出的模型函数f的偏导来拟合残差。

Staking

Bagging和Boosting的区别总结

Bagging和Boosting的区别：

1）样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

Bagging：使用均匀取样，每个样例的权重相等

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

Bagging：各个预测函数可以并行生成

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。
5）bagging是减小variance，而boosting是减小bias

为什么说bagging是减小variance，而boosting是减小bias?

模型的独立性

抽样的随机性决定了模型的随机性，如果两个模型在训练集抽样过程不独立，则两个模型不独立。
bagging中基模型的训练样本都是独⽴的随机抽样，但是基模型却不不独⽴呢?
我们讨论模型的随机性时，抽样是针对样本的整体。而bagging中的抽样是针对于训练集（整体的子集），所以并不能称其为对整体的独立随机抽样。那么独立性体现在哪里？
bagging 的抽样为两个过程：

1. 样本抽样：训练集选择
   整体模型F(X1, X2, …, Xn)中各输⼊入随机变量量(X1, X2, …, Xn)对样本的抽样
2. 子抽样： 特征选择
   从整体模型F(X1, X2, …, Xn)中随机抽取若⼲干输⼊入随机变量量成为基模型的输⼊入随机变 量

假若在⼦子抽样的过程中，两个基模型抽取的输⼊入随机变量量有⼀一定的?合，那么这两个基模型对整
体样本的抽样将不不再独⽴立，这时基模型之间便便具有了了相关性。

Bagging
Bagging对样本重采样，对每一次重采样得到的子样本训练一个模型，最后取平均。

• 基于其取样方式，其子样本集具有相似性。
• 且Bagging中的基学习器采用的是使用的是同种模型(决策树或KNN等)。

因此各模型有近似相等的bias和variance。(事实上，各模型的分布也近似相同，但不独立。)
基于数学中的期望公式：

可以看到，各个基模型的期望和整体期望近似相等，也即其Bagging后的bais与单个基模型的bias接近，所以Bagging并不能显著降低bias。
对于方差，若各子模型独立，则有：

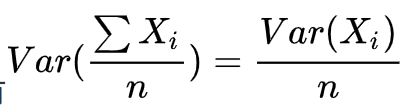
可以看到，在这种情况下，可显著降低单个基模型的variance。
若各子模型完全相同(即子模型间相关性为1时)，则有：

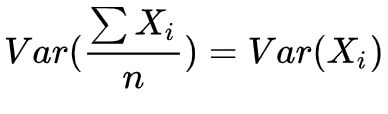
可以理解为，当所有的基模型都完全相同时，其方差必然相同，那么整体平均的方差也必然相同。此时不会降低variance.
由于bagging方法得到的各子模型是有一定相关性的(各训练数据之间是有关系的)，属于上面两种极端状态的中间态，因此一定程度可降低variance。
所以增加基模型n的数量，整体模型的方差减少，从而防止过拟合能力增强，准确度提高。但是，模型的准确度⼀一定会⽆无限逼近于1吗?并不不⼀一定。当基模型增加到一定数量后，各基模型的方差的改变趋近于极限，准确度达到极限。

 因此，Bagging要求基模型必须是强模型，否则就会导致 整体模型的偏差度低，即准确度低。

Random forest
为了进一步降低variance，Random forest 通过随机选取变量做拟合的方式(即特征选择随机)，在树的内部节点分裂过程中，不在是针对所有特征，而是随机抽样一部分特征纳入分裂的候选项。
使得模型的相关性降低，整体variance进一步降低。
boosting
boosting的构建就是通过不断学习前一个基模型的残差，达到整体的加强效果。因此其作为是可以降低整体模型的偏差，准确度提高。
但是准确度一定会无限逼近于1吗？仍然并不一定，因为随着训练的进行，整体模型的方差变大，导致防止过拟合的能力变弱，最终导致了准确度反而有所下降，可能会造成过拟合。
对于方差，由于采用串行的迭代算法策略，各基模型之间是强相关的，于是各基模型之和并不能显著降低variance。
因此boosting主要靠降低bias提高精度，这也就要求各基模型必须为弱模型(偏差高方差低)。

基于boosting框架的Gradient Tree Boosting模型中基模型也为树模型，同Random Forrest，我 们也可以对特征进⾏行行随机抽样来使基模型间的相关性降低，从⽽而达到减少⽅方差的效果。

参考

https://www.cnblogs.com/earendil/p/8872001.html