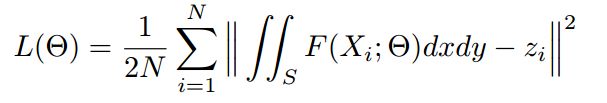MCCN算法:Single-Image Crowd Counting via Multi-Column Convolutional Neural Network
论文:《Single-Image Crowd Counting via Multi-Column Convolutional Neural Network》
原文链接:论文原文链接
前言
作者提出的方法希望可以准确地估计任意人群密度和任意视角的单张图片。因此设计了一种多列卷积神经网络结构。提出的方法可以允许任意尺寸和分辨率的图片。利用不同尺寸滤波器的感受野,每列CNN能够适应由于视角或图像分辨率造成的人或头部的尺寸变化去学习特征。基于几何自适应核函数,不需要知道输入图像的透视图,可以精确地计算出真实的密度图。另外作者开源了Shanghaitech数据集,该数据集分文part-A和part-B两部分。数据集的详细描述见下文。
相关工作
人群计数的方法大体包括两类方法。早期的方法是基于检测的方法,通常假设人群是由单个实体组成,可以被指定的检测器检测到。这种基于检测的方法的局限性在于,在聚集环境或非常密集的人群中,人群之间的遮挡会显著影响检测器的性能,从而影响最终的估计精度。
人群计数最广泛使用的方法是基于特征的回归。这类方法的主要步骤是:
1)前景分割
2)从前景中提取各种特征,如人群掩膜面积、边缘计数、或者纹理特征。
3)利用回归函数估计人群数。
线性或分段线性是函数是相对简单的模型,具有良好的性能。其他更高级有效的的方法包括岭回归(RR),高斯过程回归(GPR),和神经网络。
本文的贡献
人群密度估计所存在的问题和挑战:
1,前景分割不可缺少,然而前景分割得不准确对计数结果影响很大。作者的的工作中,图像视角是任意的没有任何场景几何或移动信息。几乎不可能准确地从背景中分割出人群。因此作者没有采用分割前景来估计人群数。
2,人群的密度分布变化大,通常每张图中的大部分人存在遮挡问题,因此在传统的基于检测的方法在这种图片和场景中是无效的。
3,由于图片中人的尺度变化比较大,需要利用不同尺度的特征为不同图片进行准确地人群密度实数。由于作何没有跟踪特征,并且很难手工制作出适用于所有不同尺度的特征,所以作者采用能够自动学习有效特征的方法。
针对这些问题,作者提出了一种多列卷积神经网络(MCNN),可以对任意静态图的人群进行计数。作者的MCNN包含三列卷积神经网络,它们的卷积核尺寸不同。MCNN的输入时一张图片,输出时一张人群密度图,它的积分给出了图片的总人数。
具体的贡献如下:
1)采用多列卷积结构的原因非常自然,三列神经网络对应的卷积核尺寸不同(大、中、小)所以具有不同的感受野。由于透视效果或不同的图像分辨率,每列卷积卷积网络学习到的特征能够适应人/头的尺寸变化。
2)采用1*1的卷积核代替了全卷积网络,因此模型的输入图片size可以是任意的,从而避免失真。网络的即时输出时人群密度的估计,可以从中得到总体人数。
3)收集了一个新的数据集来评估人群密度估计方法。
现有的人群计数数据集不能完全测试算法,作者考虑了不同场景中的性能,因为它们在视角变化(UCSD, WorldExpo ' 10)、人群计数(UCSD)、数据集规模(UCSD, UCF CC 50)或场景变化(UCF CC 50)方面存在限制。因此,作者开源了他们的数据——Shanghaitech数据。该数据集包含part-A和part-B两部分。其中part-A使用网络上爬取下来的图片,而part-B是来源于上海的商业街。作者在四个数据集上进行了实验,这四个数据集的分布如下表所示:
MCNN网络
a,基于人群计数的密度图
通过卷积神经网络估计指定图片中人的数目有两种方法。一是网络输入一张图片,然后输出图片中的人头数估计。另一种是输出人群的密度图(即每平方米中有多少人)然后通过积分获得人头数。作者采用第二种方法,原因如下:
1)密度图保留了更多的信息。对比人群的总数,密度图给出了图片中人群的空间分布,这种分布信息在许多应用中是非常有用的。例如,如果一片小区域的密度远高于其他区域,那么可能暗示着那儿发生了一些异常。
2)通过CNN学习密度图,所学习的滤波器更适合任意大小的头。因此,该滤波器更具有语义意义,从而提高了人群计数的准确性。
b,通过几何自适应核函数生成密度图
训练图片的密度质量很大程度决定了方法的性能。作何先描述如何把标注人头的图片转化为人群密度图。
如果在 Xi i处有人头,则把它表示为 δ(x - xi)。因此对于一张具有N个标记人头的图片可以用下面的函数表示:
为了把它转化为连续函数,作者把它和高斯核函数 ![]() 进行卷积操作。因此,密度函数为
进行卷积操作。因此,密度函数为 ![]() 然而,这个密度函数是假设这些 xi (人头)是图片中独立的样本,但实际并不如此。实际上,每个xi代表三维场景中地面上的人群密度样本,由于视角畸变,不同样本xi对应的像素对应场景中不同大小的区域。
然而,这个密度函数是假设这些 xi (人头)是图片中独立的样本,但实际并不如此。实际上,每个xi代表三维场景中地面上的人群密度样本,由于视角畸变,不同样本xi对应的像素对应场景中不同大小的区域。
因此,为了精确估计人群密度函数F(x),作者需要考虑畸变(由地平面和图像平面引起的単应性畸变)。不幸的是,对于可用的数据集,我们通常不知道几何场景。然而,如果假设每个头部周围的人群分布比较均匀,那么头部与其最近的k个邻居之间的平均距离(在图像中)给出了一个合理的几何失真估计(由透视效果引起)。
因此作者需要为图片中的每个人基于头部size确定扩散参数σ。然而,在实际应用中,由于很多情况下的遮挡,几乎不可能准确地得到头部的大小,而且也很难找到头部大小与密度图之间的潜在关系。有趣的是,作者发现在拥挤的场景中,头部的大小通常与相邻两个人中心的距离有关(请参见图2)。作为一种折衷,对于那些拥挤场景的密度图,作者建议根据每个人与其邻居的平均距离来自适应地确定每个人的扩散参数σ。
对于给定图片中人头Xi,定义它的最近k个距离为 ![]() 。可以得到平均距离
。可以得到平均距离 ![]() 。因此,与Xi 相关的像素对应场景中地面的一个区域,其半径大致与
。因此,与Xi 相关的像素对应场景中地面的一个区域,其半径大致与 ![]() 成比例。因此为了估计像素 Xi 附近的人群密度,作者把脉冲函数
成比例。因此为了估计像素 Xi 附近的人群密度,作者把脉冲函数![]() 和高斯核函数进行卷积,方差
和高斯核函数进行卷积,方差 ![]() 和
和 ![]() 成正比。确切的密度函数为:
成正比。确切的密度函数为:
具体的,作者将标记H与与每个数据点周围的局部几何形状相适应的密度核函数进行卷积操作,称为几何自适应核。实验中,根据经验发现 β=0.3时能得到最好的结果。
原始图片通过卷积上自适应高斯核函数生成的人群密度图如下:
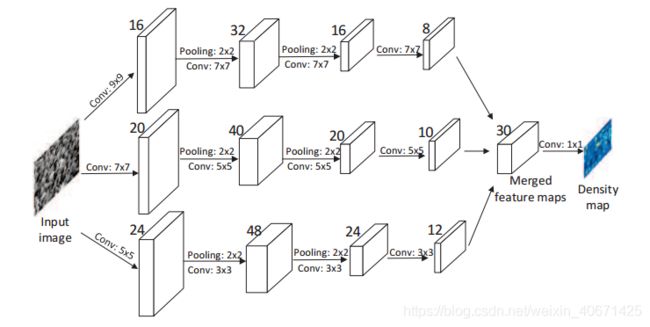
MCNN网络结构
由于透视失真,图像通常包含非常不同大小的头部,因此具有相同大小感受野的滤波器不太可能捕捉到不同尺度下人群密度的特征。因此,很自然地使用具有不同大小的局部感受野的过滤器来学习从原始像素到密度图的映射。对于MCNN中的每一列网络,作者使用不同尺度的滤波器对不同尺度人头进行密度图建模。例如,具有大感受野的滤波器对对人头较大的密度图建模更加有用。具体的网络结构如下。
MCNN包含三路并行的CNN,每个CNN具有不同尺寸的局部感受野。为了简单起见,对每一列都采用同样的网络结构(卷积-池化-卷积-池化),区别只在于卷积核的尺度和数量。采用2*2的最大池化和ReLU作为激活函数。为了减少计数复杂度,作者对尺度较大的卷积核采用较少的数目。对于每列CNN的输出特征图,把他们堆叠起来(通道级联)然后把堆叠得到的特征图映射成密度图。为了把特征图映射成特征图,作者采用1*1的卷积核。利用欧式距离来衡量ground truth和估计密度图。损失函数计算如下:
Θ是MCNN中的可学习参数集,N是训练图片数目,Xi是输入图片,Fi是图片xi的GT密度图。F (Xi; Θ)表示由MCNN生成的估计概率密度,L是是GT概率密度图和估计密度图的损失。
相关细节:
1)采用两层最大池化,分辨率变为原图的四分之一。在训练阶段,在生成图片的密度图之前,同样下采样率为四分之一。
2)CNN通常归一化输入图片到同样的尺寸,作者采用输入图片的原始尺寸,因为把图片resize到同样的尺寸会给密度图引入额外的失真这样会很难进行估计。
3)除了每列CNN具有不同尺寸的滤波器,和MDNN的另外一个区别是,MCNN把每列CNN输出的特征图利用可学习的权重整合到一起(例如1*1的卷积核,相当于做了特征融合)。对比MDNN,它只把输出进行平均操作。
MCNN的优化
损失函数可以通过基于batch的随机梯度下降和反向传播进行优化。然后实际中,由于训练样本非常有限和神经网络的梯度消失效应,很难同时学习所有的参数。作者单独对每一列CNN进行预训练,直接把第四层的卷积映射为密度图。然后利用这些预训练的CNN初始化每一列CNN,然后同时fine tune每一列的所有参数。
迁移学习
MCNN的优点是用可习的滤波器建模不同尺度的人头密度图,因此如果模型在包含不同尺度人头的数据上进行训练,那么模型能够很好地适应另外一个具有类似尺寸的密集人头。如果目标域只包含一少部分训练样本,我们可以简单MCNN的前面几层网络并且只fine tune最后几层卷积网络。fine tune最后几层卷积网络有两个有优点。
1)固定前面几层在源域学到的知识可以被保留下来,fine tune最后几层模型可以适应目标域,因此源域和目标域的知识可以被整合到一起帮助改善准确率。
2)对比fine tune整个网络,fine tune最后几层可以大大减少计算复杂度。
实验
评价指标采用了绝对误差(MAE)和均方误差(MSE),具体公式如下:
Shanghaitech数据集的统计分布
数据增强
作者从每张图片的不同位置裁剪了9个patches,每个patches是原始图片的四分之一,利用所有的patches来训练模型提高模型的泛化能力。
part-A数据的实验结果可视化
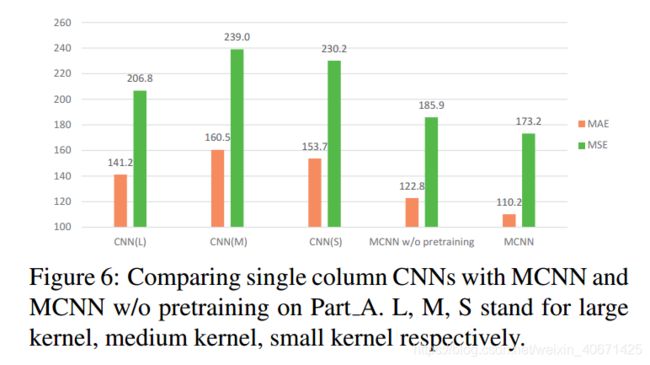
另外作者做了一些消融实验来证明预训练、单列CNN(大、中、小的卷积)和不同的损失函数对于MCNN效果对比。
除了直接把图片映射成密度图,也可以把图片映射成总总人头数。对输入图片 ![]() 的总人头数为
的总人头数为 ![]() ,
,![]() 表示估计密度图,Θ是MCNN的参数,可以获得下面的目标函数 :
表示估计密度图,Θ是MCNN的参数,可以获得下面的目标函数 :
S代表所估计的密度图的空间区域
在开源数据集上取得的实验结果