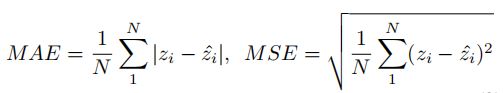2016Single-Image Crowd Counting via Multi-Column Convolutional Neural Network论文笔记

Abstract

1.单张图片、任意人群密度、任意视角
2.提出MCNN网络将图片映射到人群密度图
3.输入图片任意大小、任意分辨率，利用不同尺寸的感受野适应视角影响、图片任意分辨率。
4.基于几何自适应核计算密度图（改进密度图）

1.Introduction

Related work

别人的方法

1.较早的方法：帧间探测器detector，基于外表、运动特征
缺点：遮挡严重、人群密集不适用。
2.簇轨迹，基于跟踪视觉特征
KTL跟踪器+聚类；
缺点：不能计算静止人群。
3.基于特征回归：
主要步骤：1)前景分割；2）提取前景特征（面积特征、边缘特征、纹理特征）；3）利用回归函数估计人群数。线性函数或分段线性函数是针对简单的模型，可以产生良好的性能。还有Ridge regression（RR）、Gaussian process regression（GPR）和神经网络（NN）。
4.针对静止图片的人群计数
【12】利用多信息源估算单张图片极其密集的人数，并提出UCF_CC_50数据集（50张图片标注64000人）；【2】接着将来自多源信息，即兴趣点(SIFT)、傅里叶分析、小波分解、GLCM特征和低信任度探测仪；【28】利用预训练CNN提取的特征训练SVM。
5.近来Zhang【33】提出了针对不同场景的CNN方法。选择相似场景的图片微调网络。
缺点：训练集和测试集都需要透视图，而透视图是不易得到的。

自己的方法

面临的挑战：

1.前景分割不好，会影响人群计数。
2.遮挡严重，人群密度分布变化大，致使基于检测的方法效果不好。
3.人群尺度变化，我们使用的是不同尺寸大小的特征。由于不同的尺寸，很难人工标注特征，必须自动学习特征。

受【8】（用多列深度网络进行分类）启发，提出MCNN方法。他们的模型进行训练根据不同方法取得列数不同。我们是有三列，每列的卷积核不同大小。输入是一张图片，输出是对应的人群密度图，积分得到人数。
论文贡献：

1. 三列中不同大小（大、中、小）感受野的滤波器解决不同尺度的人头大小和图片分辨率的问题。
2. MCNN中我们用1*1卷积核的卷积层代替全连接层，使得输入图片是任意大小。
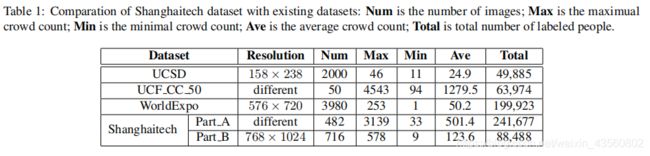
3. 提出Shanghaitech数据集，因为已有的数据集不满足不同场景的要求。（大约1200张图片，33万人有标签）。数据集包含两部分Part A and Part B，其中Part A是从网上找的，人数较多；Part B来自上海繁华地区的街道。

2.Multi-column CNN for Crowd Counting

2.1. Density map based crowd counting

选密度图的原因：（1）保留信息多，如空间分布信息；（2）滤波器更加适应不同尺寸的人头。

2.2. Density map via geometry-adaptive kernels

给定训练集的密度图决定了我们方法的表现。如何将一张带标签人头的图片转换为一张密度图？
N个人头被标记的图片表示方法：

xi是人头所在像素点。
把这个图片变成连续密度函数，将此函数与高斯内核进行卷积。密度函数就是F(x) = H(x) ∗ Gσ(x)，然而这个密度函数是假设xi是独立样本，而事实并非如此。事实上，xi是真实三维场景地面上的样本，由于透视形变，xi对应于场景中不同大小的区域。因此为了精确估计人群密度F，我们将地面与照片平面之间的形变考虑在内。然而我们不知道场景中的几何关系。所以，我们假设人群是正态分布的，这样用人头和他K个邻居的平均距离来估计几何形变。

因此我们应该根据图像中每个人的头部大小来确定传播参数σ。但是实际上，由于遮挡很难得到人体头部的大小，人头大小与密度图之间的潜在联系也很难确定。我们发现，人头的大小与两个邻居中心点的距离有关。折中一下，我们提出由人与其周围邻居的平均距离来确定传播参数σ。

对于图片中的每个人头所在位置xi，它与周围K个邻居的距离分别为，平均距离为。与xi相关联的像素对应于场景中地面上的一个区域，其半径大致与di成正比。

密度函数F如下：

换句话说，我们将标签H与每个点的几何自适应密度核卷积。实验中我们发现β = 0.3时效果最好。

2.3. Multi-column CNN for density map estimation

同样大小感受野不可能得到不同尺寸的人群密度特征。受【8】MDNNs启发，我们用多列CNN学习目标密度图。大的感受野学习较大的人头的密度图更好。
包含3列平行的CNN，每列滤波器大小不同。为了简化，我们对于每列都是用相同的网络结构，不同点是滤波器的大小和数量。最大池化是2*2，激活函数是Rectified linear unit (ReLU)。我们将所有CNN的输出特征映射叠加起来，并将它们映射到密度图中。

欧式距离测量真实图和预测图的距离。损失函数如下：

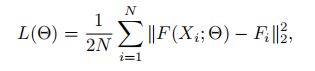
Θ是MCNN的学习参数，N是训练图片数，Xi是输入图片，Fi是真实密度图，F(Xi; Θ)是预测值。
注：

1. 两次最大池化使得每张图片空间分辨率减少为原来的1/4，所以训练阶段对每张图下采样1/4.
2. 输入网络中为原图尺寸，不需要归一化。
3. MCNN将CNN输出用1*1卷积核加在一起，MDNN是取得平均值。

2.4. Optimization of MCNN

损失函数的优化是通过批处理的随机梯度下降和反向传播。所有参数同时学习是很难得到的，受【11】RMB预训练成功的影响，直接映射第四卷积层的输出到密度图。我们用预训练的CNN初始化所有列，对所有参数同时进行微调。

2.5. Transfer learning setting

由于MCNN学习的是不同大小的人头，因此很容易转到另一个部分尺寸大小相同的其他数据集上。如果目标域训练样本少，可以修改每一列的前几层，只需要微调最后几层卷积层。微调最后几层的优点：（1）可以保留在源域学习的知识，模型可以适应目标域。因此可以集成源域和目标域的知识，提高精确度。（2）减少计算复杂度。

3. Experiments

对比试验：3个已有的数据集+自己的

3.1Evaluation metric

MAE体现准确性，MSE体现鲁棒性。

3.2 Shanghaitech dataset

Part_A 482张，其中300张训练182张测试；（网上搜集）
Part_B 716张，其中400张训练316张测试；（街道，较稀疏）

为增加训练数据，我们从不同位置选取9块1/4大小的patch。对于Part_A密度大，使用几何自适应卷积核生成真值图，预测密度重叠的部分取平均值。Part_B人少，使用高斯卷积核生成真值图。实验中，我们先预训练MCNN每一列，然后再微调整个网络。

1、LBP+RR：
Part_A被分成8X8的block，Part_B被分成12X16block，每个block得到了59维LBP特征，所以LBP特征连在一起表示这幅图片。真值图就是64D或者192D向量。

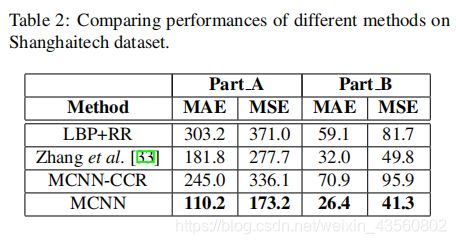
MCNN预训练的效果、单列CNN vs MCNN：

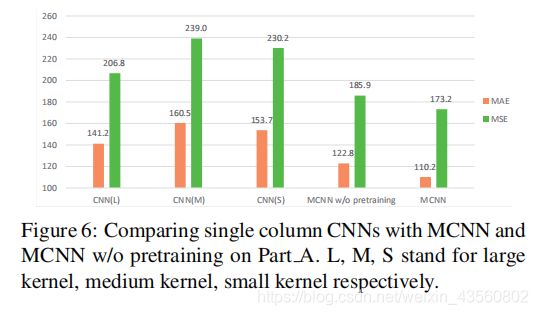
2、不同损失函数（MCNN-CCR）：
输入图片Xi (i = 1, . . . , N)，总人数zi，F(Xi
; Θ)预测密度图，

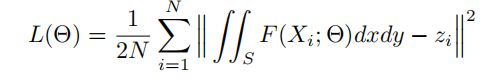
S表示预测密度图的空间域，真值密度图没有用到。
3、 Zhang et al. [33]：
把A和B按人数分成10个组，Part_A182张测试，其中（前9组）18张+（第十组）20张，Part_B316张测试，其中（前9组）31张+（第十组）37张，

3.3. The UCF CC 50 dataset

50张图片，变化极大，由Idrees et al. [12]提出。我们采用5折交叉验证。

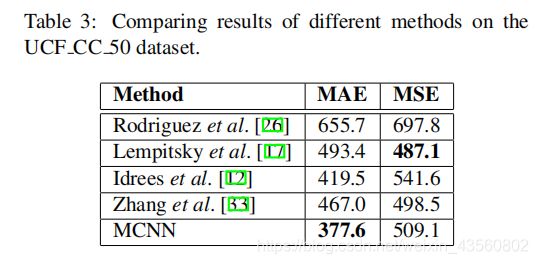
Rodriguez et al. [26]采用密度图计算人数，Lempitsky et al. [17]采用随机Patch的dense SIFT 特征和MESA距离。Idrees et al. [12]采用multi-source特征计算人数，Zhang et al. [33]使用CNN模型。

3.4. The UCSD dataset

UCSD大学监控的2000帧图片，10fps，图片大小158*238，由【4】提出。每张图片大约平均25人，数据集提供帧图片ROI。我们follow【4】，取601-1400训练，其余测试。由于人群不满足正态分布前提假设，So we fix the σ of the density map.ROI外的像素置为0，我们用ROI修改最后一层卷积层。下图说明我们的方法也适用于人数相对较少的场景。

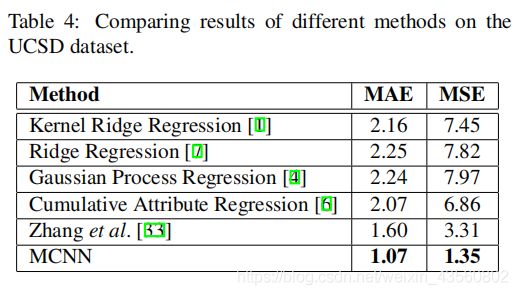
3.5. The WorldExpo’10 dataset

由 Zhang et al. [33]提出，来源于2010上海世博会的108个监控的1132个已标注的视频。作者提供3980帧标注好199923个人头，3380帧作为训练，用5个不同场景的视频作为测试集，每个视频是已被标记的120帧。测试场景的ROI被给出。

follow【33】,根据透视图生成密度图σ = 0.2 ∗ M(x)。M(x)表示实际一平方米对应图片中的像素数。我们基于ROI mask修改了最后一个卷积层，即将与ROI区域对应的神经元设置为零。

3.6. Evaluation on transfer learning

为了证明迁移能力，我们使用 the Part A of Shanghaitech dataset作为源领域（source domain），使用 the UCF CC 50 dataset 作为目标领域。具体就是，使用源领域来训练MCNN模型。为了算出目标领域的人数，我们提出两种情况：（1）训练时，没有目标场景的样本；（2）训练时，加入少许目标场景的样本。case(1)我们直接用Part_A of Shanghaitech dataset训练好的模型；case(2)我们用目标域样本微调网络。

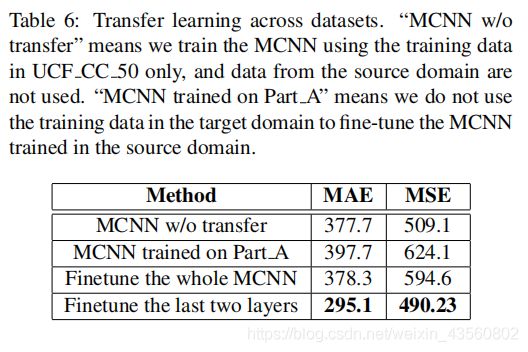
UCF_CC_50和Part_A的准确率是接近的（377.7vs397.7），意味着Part_A的模型用于UCF_CC_50是可行的。

微调最后两层和微调全部网络表现差异的原因在于限制了UCF_CC_50的训练样本。微调最后两层确保适应目标源，前面不变又确保充分学习源目标的特征。但是整个网络被调整，效果就类似于只用目标场景去训练。

4. Conclusion

提出MCNN可以估计任意视角单张图片的人数