超低能解读群论

葱花的超低能解读群论 QUQ ，弱哭了1551

前排鸣谢：
（PY关系）指导：@Psyduck （日常%）大jiu~佬：@hdxrie

推荐视频：嘿嘿嘿

目录

一、群的定义

二、群的模型与置换群

三、Burnside引理 和 Pólya定理

四、例题 Poj1286 Necklace of Beads

一、群的定义

群是***一些定义的映射*** 对于***指定的有限集合*** 的集合；

其中群必须满足以下性质：

• 封闭性：集合内元素间的映射不会超过指定的有限集合；

• 结合律：集合内元素间的映射满足结合律；

• 单位元：集合内存在一个基底元素，使得集合内所有的元素都可以用基底元素表示；

• 逆元：集合内必定存在成对的元素，使得经过一些定义的映射成为基地元素。

更严格地讲，群的定义为：

注意群是***映射的集合*** 不是 一些定义的映射 +指定的有限集合 。

一个简单的例子：

实数的加法就是一个群（实数加法群）

• 一些定义的映射： +，-（加一个负数）；

• 指定的有限集合： 全体实数；

• 封闭性：一个实数加上一个实数还是一个实数；

• 结合律：a,b,c为实数，则：$(a+b)+c=a+(b+c)$

• 单位元：0；

• 逆元：a为实数，那么a与-a互为彼此的逆元，即：$a+(-a)=0$

然后举一个复杂一点点的例子，以后我们也会用到这个举例：

对于以下集合：（多种正方形）

我们定义8种映射关系：

易证得，这***8种映射关系*** 对于这个***正方形集合*** 满足：

封闭性，结合律，单位元(1号正方形)，逆元(2与4,5与5等)；

所以这个映射的集合为群。

具体证明不再赘述。

二、群的模型与置换群

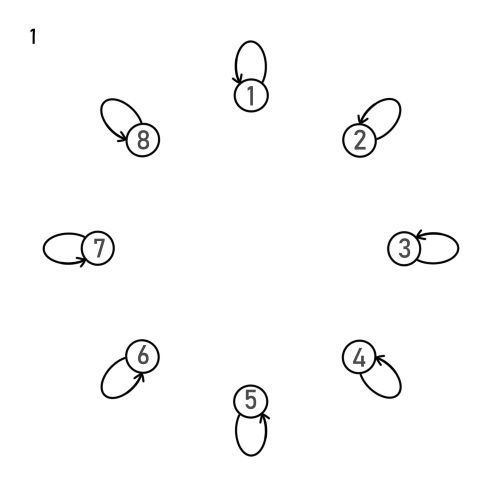
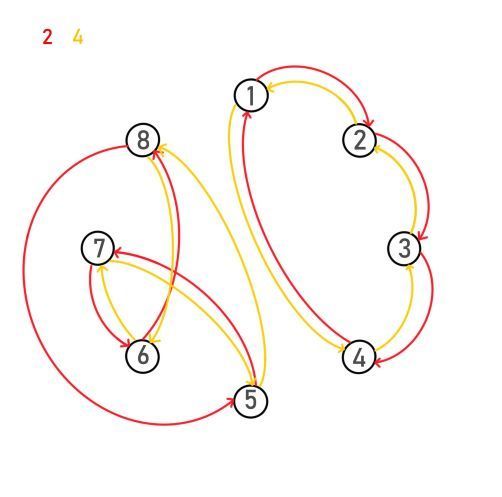
对于第一部分下面这个集合：

我们可以发现：

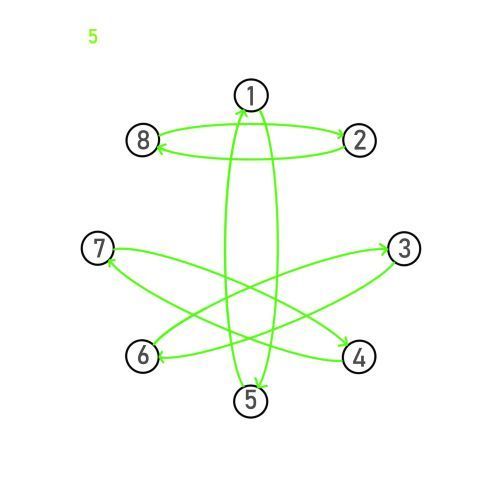
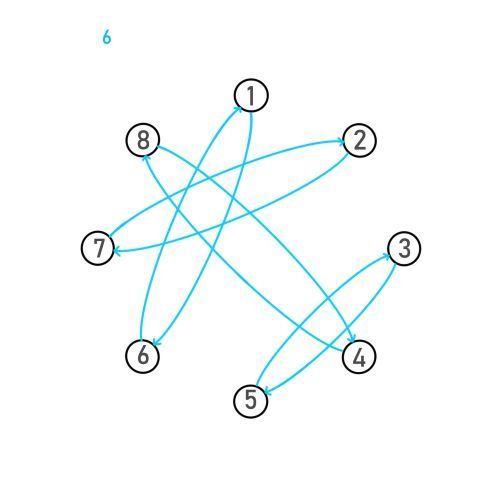
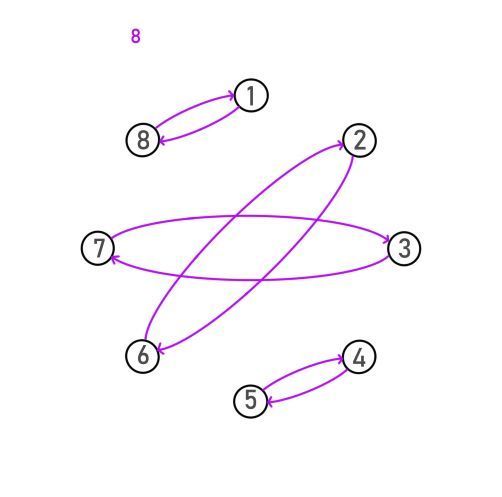
这个群的模型满足一个基本的有向图模型

我们不妨把它建立出来观察一下它的性质：

（边是映射，点是集合内元素，左上角是映射的类型在图上的颜色）

看起来很美好，对不对(彩虹！！)？

有点乱？我们可以分开看看：

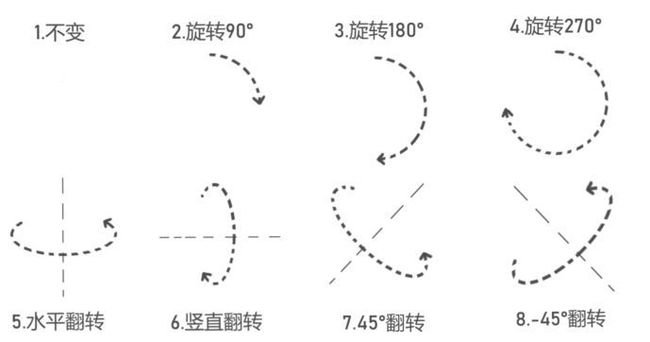
1. 不变

2. 旋转90°

3. 旋转180°

**4. 旋转270° **

5. 水平翻转

6. 竖直翻转

7. 45°翻转

8. -45°翻转

充分满足对称性的美好 (彩虹！！)

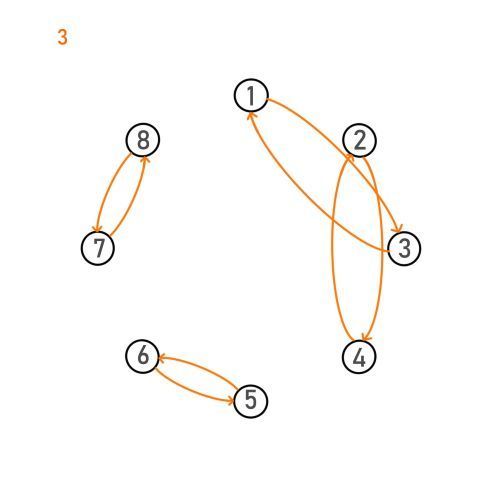
我们可以很轻松观察出这个映射集合的封闭性。

结合律也可以被轻松观察出来看出来，就不举例子了：

逆元就更显而易见了，除了2和4互为逆元，其他的映射都为自己的逆元：

下面我们带入一个新的概念：置换和置换群

直接上学长的ppt(%%%)

简单点说，上面我们举例的群，它的八种映射方式，就是置换；

而8种置换组成的群，就是置换群；

我们举一个例子……hummmm……就比如：

5. 水平翻转

它的置换写法就是：

$$\left(\genfrac{}{}{0ex}{}{12345678}{58671342}\right)$$

这不就是模型中有向图的边吗？

很简单？对吧？

那么现在，我们可以进入重点咯？

三、Burnside引理 和 Pólya定理

先直接甩Burnside引理的定义：(还是学长的pptOrz)

看上去挺复杂的？我们慢慢来吧。

先引入一个简单的概念：循环

下面我们直接举个例子：置换的循环分解

上一节末尾的例子：

5. 水平翻转

它的置换写法是：

$$\left(\genfrac{}{}{0ex}{}{12345678}{58671342}\right)$$

解出来的循环就是：$$(15)(28)(36)(47)$$

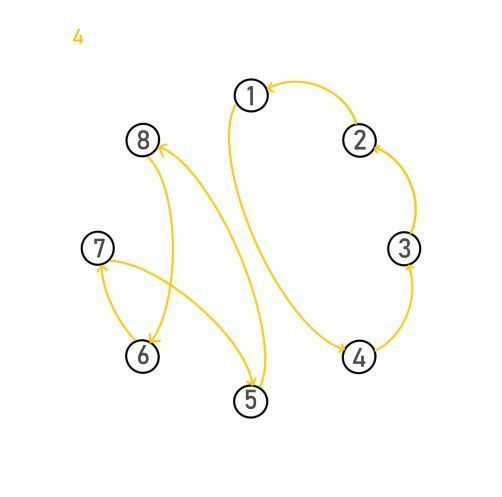
放回模型看看呢？我们可以发现：

置换的循环分解就是模型中有向图的强连通分量

不如我们再放两个例子呢？

4. 旋转270°

它的置换写法就是：

$$\left(\genfrac{}{}{0ex}{}{12345678}{41238756}\right)$$

分解出来的循环就是：$$(1432)(5867)$$

1. 不变

它的置换写法就是：

$$\left(\genfrac{}{}{0ex}{}{12345678}{12345678}\right)$$

分解出来的循环就是：$$(1)(2)(3)(4)(5)(6)(7)(8)$$

看样子我们的想法没有问题；

那么，现在我们重新给出Burnside引理的内容：

设置大小为$|G|$，由$g$组成的群$G$，作用于有限集合$X$上面，那么$X$在$G$内映射的作用下，$X$的变换结果有这么多种：

$$\frac{{\sum }_{g\in G}^{}X(g)}{|G|}$$

其中$X(g)$为映射$g$对与集合$X$的操作结果

现在，是不是清楚很多了呢(雾)？

不过我们发现，这个方法的复杂度特别高，不仅要枚举每一个映射，还要对每种映射枚举一次每个置换，所以引入Pólya定理：

先甩定义：

即：

设置大小为$|G|$，由$g$组成的群$G$，作用于$k$组合成的有限集合$X$上面，那么$X$在$G$内映射的作用下，$X$的变换结果种类有这么多：

$$\frac{{\sum }_{g\in G}^{}{k}^{m(g)}}{|G|}$$

其中$m(g)$为映射$g$对与集合$X$的操作结果

也就是把$X(g)$优化成了$k^{m(g)}$ ，减少了枚举操作。

其中$m(g)$可以$O(n)$求，这个很简单，就是求一个有向图的强连通分量，就不举例子了。

四、例题 Poj1286 Necklace of Beads

Necklace of Beads

Time Limit: 1000MS Memory Limit: 10000K

Description

Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 24 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there?

Input

The input has several lines, and each line contains the input data n.
-1 denotes the end of the input file.
Output
The output should contain the output data: Number of different forms, in each line correspondent to the input data.

Sample Input

4

5

-1

Sample Output

21

39

题目大意：对于指定n，求得到红，绿，蓝三种颜色珠子串成的长度为n的项链有多少种(首尾相接)

我们先来看一下这个群的映射方式：

旋转，翻转。

我们之前举的例子呢，刚好和$n=4$的情况差不多，建议各位读者巨佬可以自己画一下其他情况的草图仔细观察一下，我们可以发现具体群内的映射有如下规律：

旋转一共有$n$个角度，顺时针旋转$i$格的置换中，每个循环的长度为$\frac{n}{\mathrm{g}\mathrm{c}\mathrm{d}(i,n)}$，个数为$\mathrm{g}\mathrm{c}\mathrm{d}(i,n)$；

旋转共有$n$个对称轴，所以当$n$为奇数时，每一个对称轴都有$\lceil \frac{n}{2}\rceil$个循环；当$n$为偶数时，有一半的对称轴有$\frac{n}{2}$个循环，一半有$\frac{n}{2}+1$个；

利用Pólya定理，我们可以得到答案应该为如下公式：

当$n$为奇数：

$$ans(n)=\frac{{\sum }_{i=1}^n{3}^{\mathrm{g}\mathrm{c}\mathrm{d}(i,n)}+n\times 3^{\lceil \frac{n}{2}\rceil }}{n+n}$$

当$n$为偶数：

$$ans(n)=\frac{{\sum }_{i=1}^n{3}^{\mathrm{g}\mathrm{c}\mathrm{d}(i,n)}+\frac{n}{2}\times 3^{\frac{n}{2}}+\frac{n}{2}\times 3^{\frac{n}{2}+1}}{n+n}$$

那么代码实现就非常简单了：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long power(long long a,long long b){
	long long ans=1ll;
	while(b){if(b&1ll)ans*=a;a*=a;b>>=1;}
	return ans;
}
long long gcd(long long a,long long b){return b?gcd(b,a%b):a;}
long long n,g,ans;
int main()
{
  while(scanf("%lld",&n)==1&&n!=-1){
    if(n==0){printf("0\n");continue;}
    ans=0;
    for(int i=1;i<=n;++i)g=gcd(n,i),ans+=power(3,g);
    if(n&1)ans+=n*power(3,(n+1)>>1);
    else ans+=(n>>1)*power(3,(n+2)>>1),ans+=(n>>1)*power(3,n>>1);
    ans=ans/(n<<1);
    printf("%lld\n",ans);
  }
  return 0;
}

感谢水本大jiu_{蒻的博客QUQ，1551}