数据结构回顾——排序
要求:掌握算法思想,性能分析,代码实现
注:本文默认递增排序
一,排序的基本概念
1,什么是排序:将一个没有顺序的数列进行重新排列是它成为一个递增(递减)序列
2,稳定性:如果数列中有两个元素的值是相等的,排序后他们的相对位置没有发生改变,就认为该排序算法稳定。
3,内部排序:指排序期间元素全部存放在内存中的排序
外部排序:排序期间元素无法全部同时存放在内存中,必须在排序过程中根据要求不断在内,外存之间进行移动
二,直接插入排序
插入排序:每次将一个待排序的序列插入到一个前面已经排好的子序列中
1,直接插入排序:
设已知数列[ a1 a2,,,ai,,,,an],已知a1,,,ai已经是递增序列了,如何将ai+1号元素插入到a1,,,ai中使得,它们任然是有序序列
思想:
- 找到位置k,有k前面的元素小于ai+1号元素,有k后面的元素大于ai+1号元素。
- 将ai+1元素暂存在中间变量中(空间复杂度O(1))
- 将ak,,,,ai的所有元素后移一个位置,空出ak来存放ai+1元素,后移过程中ai元素刚好替换ai+1的位置
代码实现:
void InsertSort(int A[],int n){
int i,j;
for(i=2;i<=n;i++){
A[0]=A[i];//A[0]是哨兵暂存A[i]
for(j=i-1;A[0]性能分析:
- 最好时间复杂度:O(n) 一开始就是递增的有序序列
- 平均时间复杂度:O(n2)
- 最坏时间复杂度:O(n2) 一开始就是递减的有序序列
- 空间复杂度:O(1)
- 是稳定的算法,适用于顺序存储和链式存储
2,折半插入排序
思想:对直接插入排序进行改进,将其查找插入位置k的过程由顺序查找改为折半查找
代码实现:
void BInsertSort(int A[],int n){
int i,j;
int low,high,mid;
for(i=2;i<=n;i++){
A[0]=A[i];
low=1;high=i-1;
while(lowA[0])
high=mid-1;
else
low=mid+1;
}
for(j=i-1;j>=high+1;j--)//向后移动元素
A[j+1]=A[j];
A[high+1]=A[0];//插入元素
}
} 性能分析:
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
- 是稳定算法
- 适用于顺序存储
3,希尔排序:
思想:先将排序表分割成d个形如 [i,i+d,i+2d,i+3d,,,,i+kd]的特殊子表,分别进行直接插入排序,当整个表中元素已经基本有序时,再对全体记录进行一次直接插入排序。
代码实现:
void ShellSort(int A[],int n){
int i,j;
for(int dk=n/2;dk>n;dk=dk/2){//每次步长取表长的一半
for(i=dk+1;i0&&A[0]
性能分析:
- 最坏时间复杂度:O(n2)
- 平均时间复杂度:O(n1.3)
- 空间复杂度:O(1)
- 是不稳定算法
- 适用于顺序存储
三,交换排序
1,冒泡排序:
思想:假设待排序表长为n,从后往前(从前往后)两两比较相邻元素的值,如果是逆系(A[i-1]>A[i])就交换他们,直到序列比较为止。每一趟遍历表的比较就会让一个最大(最小)元素归位,就像冒气泡一样所以叫冒泡排序。n趟比较后所以元素归位。
代码实现
void BubbleSort(int A[],int n){
int i,j,temp;
bool flag;//如果是递增序列直接跳出循环减少运行时间的标志
for(i=0;ii;j--){
if(A[j-1]>A[j]){//前面元素大于后面元素,就交换
temp=A[j];
A[j]=A[j-1];
A[j-1]=temp;
flag=true;
}
if(flag==false)
return;//是递增序列,结束循环
}
}
for(int k=0;k
性能分析:
- 最好时间复杂度:O(n) 数列是递增序列
- 平均时间复杂度:O(n2) n(n-1)/2
- 最坏时间复杂度:O(n2)
- 空间复杂度:O(1)
- 是稳定算法
- 适用于顺序存储和链式存储
2,快速排序
思想:在排序表【1,,,n】中任取一个元素pivot作为基准,通过一趟排序将待排序表划分为两个部分,pivot前面的元素均小于它,后面的元素均大于它。所以一次划分会让当前的pivot元素归位,进行对已经划分的部分进行相同操作,知道每一个元素归位。
一次划分实现思路:
- 初始化标记low为划分部分第一个元素的位置,high为最后一个元素的位置,然后不断地移动标记并交换元素
- high向前移动找到第一个比pivot小的元素,
- low向后移动找到第一个比pivot大的元素
- 交换当前两个位置的元素
- 进行移动标记,执行上述过程,直到low>high为止
代码实现:
int Partition(int A[],int low,int high){
int pivot=A[low];
while(low=pivot)
high--;
A[low]=A[high];//找到大于pivot的元素,把它存到对应要交换的位置
while(low 性能分析:
- 最好平均时间复杂度:O(n*log2n)
- 最坏时间复杂度:O(n2):已经是递增序列
- 最好平均空间复杂度:O(log2n)
- 最坏空间复杂度:O(n)
- 是不稳定算法
- 适用于顺序存储和链式存储
四,选择排序
1,直接选择排序
思想:没一趟都在后面n-i+1个待排序元素中选取关键字最小的元素,作为有序子序列的第i个元素,直到n-1趟做完,待排序元素只剩下一个。也就是每次从数量中找到最小元素取出来放到前面排序。
代码实现
void SelectSort(int A[],int n){
int temp;
for(int i=0;i性能分析:
- 时间复杂度:O(n2) 与初始序列无关
- 空间复杂度:O(1)
- 是不稳定算法
- 适用于顺序存储和链式存储
2,堆排序
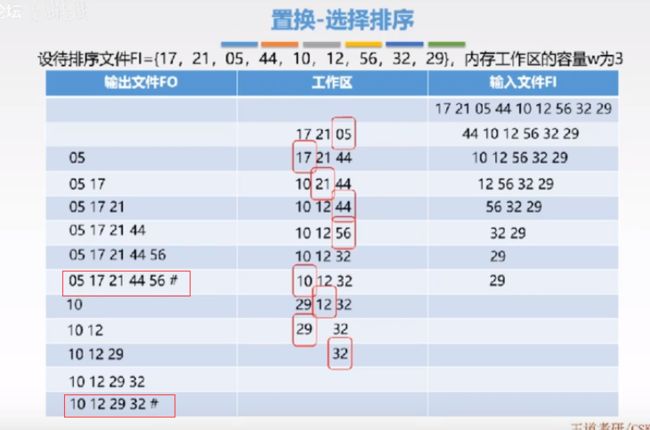
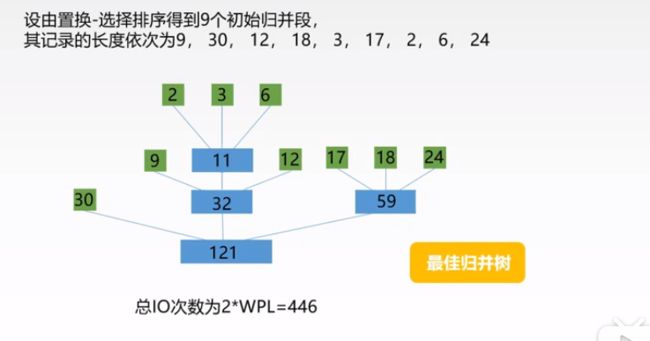
小根堆:数列中第i个元素L(i) 大根堆:数列中第i个元素L(i)>L(2i),L(i)>L(2i+1),即根节点大于两个孩子节点 大根堆的初始化: 代码实现: 性能分析: 思想:将相邻的两组序列进行有序的归并。开始时一个元素为一组,n个元素为n组,然后将相邻i号元素和i+1号元素归并成有序序列,就出现n/2组,继续对他们进行归并出现n/4组,,,,直到归为一组为止。 代码实现: (代码有问题) 性能分析: 思想:借助“分配”和“收集”两种操作对逻辑关键字进行最高位优先(MSD)和最低位优先(LSD). 以r为基数的最低位优先基数排序过程: 性能分析: 考虑的因素 外部排序通常采用归并排序的方法 r=20000/50000=4 r=3*(4+4) 3次分割才会将分成4块,4次读+4次写 S=2一共需要两次归并 T=4*Tis + 3*(4+4)*Tio +2*(20000-1)Tmg 归并的趟数=logmR + 1 (m路归并,R为初始归并段数量) 失败树:是树形选择排序的一种变形体,可以看成一棵完全二叉树,每个叶节点存放各个归并段在归并过程中当前参加比较的记录,内部节点用来左右子树中的失败者,胜利者向上继续比较,直到根节点。 S趟归并总共需要比较是次数S(n-1)(m-1)=[logmR +1]*(n-1)(m-1) =[logmR +1]*(n-1) 置换-选择排序:设初始待排文件为FI,初始归并段问阿金为FO,内存工作区为WA,内存工作区可以容纳w个记录。 思想: 最佳归并树:用来描述m归并,并且只有度为0和度为m的节点的严格m叉树 有已知序列构造m叉哈夫曼树,如果叶节点数不足,0补上 度为m的节点个数Nm=(N0-1)/(m-1),如果(N0-1)%(m-1)==0,说明这N0个叶节点可以构造m叉归并树,如果(N0-1)%(m-1)==u!说明这N0个叶节点有u个节点是多余的,补充m-u-1个节点
void AdjustDown(int A[], int k,int len){//调整节点
A[0]=A[k];//暂存该节点的值
for(int i=2*k;i<=len;i*=2){
if(i
五,二路归并排序
void Merge(int A[],int low,int mid,int high){//将相邻序列进行合并
int B[high];
for(int k=low;k
六,基数排序
七,内部排序算法的比较和应用
内部排序应用:
八,外部排序: