作业Week9、10+月模拟题3、4+CSP3、4+限时大模拟10、14
CSP3
A-瑞神的序列
1.题意:瑞神的数学一向是最好的,连强大的咕咕东都要拜倒在瑞神的数学水平之下,虽然咕咕东很苦 恼,但是咕咕东拿瑞神一点办法都没有。
5.1期间大家都出去玩了,只有瑞神还在孜孜不倦的学习,瑞神想到了一个序列,这个序列长度为n,也就是一共有 个数,瑞神给自己出了一个问题:数列有几段?
段的定义是连续的相同的最长整数序列
Input
输入第一行一个整数n,表示数的个数。
接下来一行n个空格隔开的整数,表示不同的数字
Output
输出一行,这个序列有多少段
Example
Input
12
2 3 3 6 6 6 1 1 4 5 1 4
1
2
Output
8
2.思路:该题较为简单,我们要做的操作就是判断前一个与后一个是否相同,如果不相同则最终结果ans加1.
3.代码:
#include B-消消乐大师-Q老师
1.题意:Q老师是个很老实的老师,最近在积极准备考研。Q老师平时只喜欢用Linux系统,所以Q老师的电 脑上没什么娱乐的游戏,所以Q老师平时除了玩Linux上的赛车游戏SuperTuxKart之外,就是喜欢 消消乐了。
游戏在一个包含有n 行m 列的棋盘上进行,棋盘的每个格子都有一种颜色的棋子。当一行或一列 上有连续三个或更多的相同颜色的棋子时,这些棋子都被消除。当有多处可以被消除时,这些地 方的棋子将同时被消除。
一个棋子可能在某一行和某一列同时被消除。 由于这个游戏是闯关制,而且有时间限制,当Q老师打开下一关时,Q老师的好哥们叫Q老师去爬 泰山去了,Q老师不想输在这一关,所以它来求助你了!!
Input
输入第一行包含两个整数n,m,表示行数和列数
接下来n行m列,每行中数字用空格隔开,每个数字代表这个位置的棋子的颜色。数字都大于0.
Output
输出n行m列,每行中数字用空格隔开,输出消除之后的棋盘。(如果一个方格中的棋子被消除, 则对应的方格输出0,否则输出棋子的颜色编号。
Example
Input
4 5
2 2 3 1 2
3 1 1 1 1
2 3 2 1 3
2 2 3 3 3
Output
2 2 3 0 2
3 0 0 0 0
2 3 2 0 3
2 2 0 0 0
2.思路:我们可以将输入的矩阵存成两个,之后分别判断两个矩阵中行和列是否存在可消除的元素,若存在,则将对应位置置为零。输出时,只要两个矩阵中有一个对应位置为0,就输出0,即可得到正确答案。
3.代码:
#includeC-咕咕东学英语
1.题意:咕咕东很聪明,但他最近不幸被来自宇宙的宇宙射线击中,遭到了降智打击,他的英语水平被归零了!这一切的始作俑者宇宙狗却毫不知情!
此时咕咕东碰到了一个好心人——TT,TT在吸猫之余教咕咕东学英语。今天TT打算教咕咕东字母A 和字母B,TT给了咕咕东一个只有大写A、B组成的序列,让咕咕东分辨这些字母。
但是咕咕东的其他学科水平都还在,敏锐的咕咕东想出一个问题考考TT:咕咕东问TT这个字符串 有多少个子串是Delicious的。
TT虽然会做这个问题,但是他吸完猫发现辉夜大小姐更新了,不想回答这个问题,并抛给了你, 你能帮他解决这个问题吗?
Delicious定义:对于一个字符串,我们认为它是Delicious的当且仅当它的每一个字符都属于一个 大于1的回文子串中。
Input
输入第一行一个正整数n,表示字符串长度。
接下来一行,一个长度为n只由大写字母A、B构成的字符串。
Output
输出仅一行,表示符合题目要求的子串的个数
Example
Input
5
A A B B B
1
2
Output
6
2.思路:这题主要考察思维能力,正难则反。
根据题意,可以发现不合法的串只有以下4种情况
ABB…B B
BAA…AA
AA…AAB
BB…BBA
因此分类枚举所有不合法情况,然后减去不合法的就行了。
我们可以发现当序列是AB或BA开头时,那么满足条件的子串个数就是对应序列长度减去2;而当序列是AA或BB开头时,当AA…AB或BB…A的情况时,需要额外减去1.
找到第i个元素后第一个A 和第一个B,然后分情况谈论即可(以A开头为例,B同理),如果B的位置在A之后,那就需要额外减1;如果B的位置在A之前,那就不需要额外减1;
综上所述,我们只要遍历一遍整个序列就可完成统计。
3.代码:
#include CSP4
A-TT数鸭子
1.题意:TT来到一个小湖边,看到了许多在湖边嬉戏的鸭子,TT顿生羡慕。此时他发现每一只鸭子都不一样,或羽毛不同,或性格不同。TT在脑子里开了一个map<鸭子,整数> tong,把鸭子变成了一些数字。现在他好奇,有多少只鸭子映射成的数的数位中不同的数字个数小于k。
Input
输入第一行包含两个数n,k,表示鸭子的个数和题目要求的k。
接下来一行有n个数,aiai a_iai,每个数表示鸭子被TT映射之后的值。
Output
输出一行,一个数,表示满足题目描述的鸭子的个数。
注意无行末空格

2.思路:这道题的重点是求一个数中不相同的数字个数。因此可以将这个数看成字符串,里面的每一个数字就是一个字符,设立一个大小为10的int数组.当某个数字出现的时候,这个数组的对应位置 str[ i ] - '0’处的值就为1,最后看有几个位置是1就可以得出有几个不同的数字.
3.代码:
#includeB-ZJM要抵御宇宙射线
1.题意:据传,2020年是宇宙射线集中爆发的一年,这和神秘的宇宙狗脱不了干系!但是瑞神和东东忙 于正面对决宇宙狗,宇宙射线的抵御工作就落到了ZJM的身上。假设宇宙射线的发射点位于一个 平面,ZJM已经通过特殊手段获取了所有宇宙射线的发射点,他们的坐标都是整数。而ZJM要构 造一个保护罩,这个保护罩是一个圆形,中心位于一个宇宙射线的发射点上。同时,因为大部分 经费都拨给了瑞神,所以ZJM要节省经费,做一个最小面积的保护罩。当ZJM决定好之后,东东 来找ZJM一起对抗宇宙狗去了,所以ZJM把问题扔给了你~
Input
输入 第一行一个正整数N,表示宇宙射线发射点的个数
接下来N行,每行两个整数X,Y,表示宇宙射线发射点的位置
Output
输出包括两行
第一行输出保护罩的中心坐标x,y 用空格隔开
第二行输出保护罩半径的平方
(所有输出保留两位小数,如有多解,输出x较小的点,如扔有多解,输入y较小的点)
无行末空格
2.思路:由于本题数据量较小(<=1000),因此可以直接暴力求解.
对于每一个点,求出距它最远的那个点的距离,然后找出其中最小的输出即可。
题目中要求如有多解,输出x较小的点,如仍有多解,输入y较小的点。因此只要将各点排序一下即可。
注意:最后输出的是半径的平方,不能开方。
3.代码:
#includeC-宇宙狗的危机
1.题意:在瑞神大战宇宙射线中我们了解到了宇宙狗的厉害之处,虽然宇宙狗凶神恶煞,但是宇宙狗有一个很可爱的女朋友。
最近,他的女朋友得到了一些数,同时,她还很喜欢树,所以她打算把得到的数拼成一颗树。
这一天,她快拼完了,同时她和好友相约假期出去玩。贪吃的宇宙狗不小心把树的树枝都吃掉了。所以恐惧包围了宇宙狗,他现在要恢复整棵树,但是它只知道这棵树是一颗二叉搜索树,同时任意树边相连的两个节点的gcd(greatest common divisor)都超过1。
但是宇宙狗只会发射宇宙射线,他来请求你的帮助,问你能否帮他解决这个问题
Input
输入第一行一个t,表示数据组数。
对于每组数据,第一行输入一个n,表示数的个数
接下来一行有n个数
a
i
ai a_i
a
i,输入保证是升序的。
Output
每组数据输出一行,如果能够造出来满足题目描述的树,输出Yes,否则输出No。
无行末空格。

2.思路:本题准备全遍历一下。在构造左孩子节点和右孩子节点时,都遍历各个可能的情况,但是如果每一次都这样查找的话无疑会爆掉。因此一定要合理剪枝,为此开辟了四个bool数组l1、r1和can_l、can_r。l1和r1记录对应的区间是否被遍历过,如果被遍历过那么就直接查看对应的can_l或can_r。如果没有被遍历过,那么就先遍历一下。查看其能否构造成符合标准的左子树或右子树。为了避免多余的遍历,当我们证明一个可行的建树策略后就直接结束遍历。
最后还开辟了一个二维数组result用于记录各个数据之间的公约数,避免重复的计算。
3.代码:
#includeWeek9作业
A-咕咕东的目录管理器
1.题意:建造一个目录管理器,初始时硬盘是空的,命令行的当前目录为根目录 root。目录管理器可以理解为要维护一棵有根树结构,同时每个目录的儿子必须保持字典序。并依次实现下列操作:


输出格式为:

Input
输入文件包含多组测试数据,第一行输入一个整数表示测试数据的组数 T (T <= 20);
每组测试数据的第一行输入一个整数表示该组测试数据的命令总数 Q (Q <= 1e5);
每组测试数据的 2 ~ Q+1 行为具体的操作 (MKDIR、RM 操作总数不超过 5000);
面对数据范围你要思考的是他们代表的 “命令” 执行的最大可接受复杂度,只有这样你才能知道你需要设计的是怎样复杂度的系统。
Output
每组测试数据的输出结果间需要输出一行空行。注意大小写敏感。
2.思路:题目要求一个目录能够根据子目录的名字取到它的子目录
故要用 map
MKDIR s, 创建子目录操作:因为map可以按照key也就是string就行排序,那么直接向children数组中插入名字为s的目录即可,如果已存在同名子目录返回空指针。且为了后续的撤销操作,需要将插入的子目录存储到对应的cmlist数组中,撤销时调用RM操作即可。
RM s, 删除子目录操作:与插入操作基本一致,就是改为如果不存在目录名为s的子目录返回空指针,撤销时调用addchild函数即可,addchild函数具体实现与MKDIR基本一致。
CD s, 进入子目录操作:具体操作较为简单,就是要为撤销做准备,如果执行成功就将当前的目录存储到对应的cmlist数组中,然后再更新当前目录。撤销时直接从cmlist数组取出对应的目录,然后更新now即可。
SZ和LS都较为简单,就是TREE操作需要引入一个懒更新,避免重复遍历(否则会超时),为此需要引入一个bool类型的updated来记录当前的目录是否已经遍历过以及一个vector< string>* tenDescendants来保存当前目录的十个后代;
更新可以直接通过前序遍历直接更新十个后代;也可以先更新前五个,再更新后五个以避免多余的遍历。
3.代码:
#include B-东东学打牌
1.题意:
最近,东东沉迷于打牌。所以他找到 HRZ、ZJM 等人和他一起打牌。由于人数众多,东东稍微修改了亿下游戏规则:
所有扑克牌只按数字来算大小,忽略花色。
每张扑克牌的大小由一个值表示。A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K 分别指代 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13。
每个玩家抽得 5 张扑克牌,组成一手牌!(每种扑克牌的张数是无限的,你不用担心,东东家里有无数副扑克牌)
理所当然地,一手牌是有不同类型,并且有大小之分的。
举个栗子,现在东东的 “一手牌”(记为 α),瑞神的 “一手牌”(记为 β),要么 α > β,要么 α < β,要么 α = β。
那么这两个 “一手牌”,如何进行比较大小呢?首先对于不同类型的一手牌,其值的大小即下面的标号;对于同类型的一手牌,根据组成这手牌的 5 张牌不同,其值不同。下面依次列举了这手牌的形成规则:
(1)大牌:这手牌不符合下面任一个形成规则。如果 α 和 β 都是大牌,那么定义它们的大小为组成这手牌的 5 张牌的大小总和。
(2)对子:5 张牌中有 2 张牌的值相等。如果 α 和 β 都是对子,比较这个 “对子” 的大小,如果 α 和 β 的 “对子” 大小相等,那么比较剩下 3 张牌的总和。
(3)两对:5 张牌中有两个不同的对子。如果 α 和 β 都是两对,先比较双方较大的那个对子,如果相等,再比较双方较小的那个对子,如果还相等,只能比较 5 张牌中的最后那张牌组不成对子的牌。
(4)三个:5 张牌中有 3 张牌的值相等。如果 α 和 β 都是 “三个”,比较这个 “三个” 的大小,如果 α 和 β 的 “三个” 大小相等,那么比较剩下 2 张牌的总和。
(5)三带二:5 张牌中有 3 张牌的值相等,另外 2 张牌值也相等。如果 α 和 β 都是 “三带二”,先比较它们的 “三个” 的大小,如果相等,再比较 “对子” 的大小。
(6)炸弹:5 张牌中有 4 张牌的值相等。如果 α 和 β 都是 “炸弹”,比较 “炸弹” 的大小,如果相等,比较剩下那张牌的大小。
(7)顺子:5 张牌中形成 x, x+1, x+2, x+3, x+4。如果 α 和 β 都是 “顺子”,直接比较两个顺子的最大值。
(8)龙顺:5 张牌分别为 10、J、Q、K、A。
作为一个称职的魔法师,东东得知了全场人手里 5 张牌的情况。他现在要输出一个排行榜。排行榜按照选手们的 “一手牌” 大小进行排序,如果两个选手的牌相等,那么人名字典序小的排在前面。
不料,此时一束宇宙射线扫过,为了躲避宇宙射线,东东慌乱中清空了他脑中的 Cache。请你告诉东东,全场人的排名
Input
输入包含多组数据。每组输入开头一个整数 n (1 <= n <= 1e5),表明全场共多少人。
随后是 n 行,每行一个字符串 s1 和 s2 (1 <= |s1|,|s2| <= 10), s1 是对应人的名字,s2 是他手里的牌情况。
Output
对于每组测试数据,输出 n 行,即这次全场人的排名。
2.思路:通过分析8种牌型,我们可以知道为了比较各种牌,我们除了要知道这五张牌的牌型外,还要知道sum, p1, p2三个排序关键字,其中sum是5张牌种个数为1的牌的数值和;当牌型为两对时,p1记录的是两对种较大的那一对的数值,p2记录的是两对中较小的那一对的数值;当牌型为三带二时,p1记录的是三条的数值,p2记录的是一对的数值;依次类推,p1记录的始终是比较优先级更高的数值。然后重载<,依次按照牌型,p1,p2,sum降序排列,如果前四者都相同,则按照名字的字典序升序排列。
3.代码:
#include C-签到题
1.题意:SDUQD 旁边的滨海公园有 x 条长凳。第 i 个长凳上坐着 a_i 个人。这时候又有 y 个人将来到公园,他们将选择坐在某些公园中的长凳上,那么当这 y 个人坐下后,记k = 所有椅子上的人数的最大值,那么k可能的最大值mx和最小值mn分别是多少。
Input
第一行包含一个整数 x (1 <= x <= 100) 表示公园中长椅的数目
第二行包含一个整数 y (1 <= y <= 1000) 表示有 y 个人来到公园
接下来 x 个整数 a_i (1<=a_i<=100),表示初始时公园长椅上坐着的人数
Output
输出 mn 和 mx
2.思路:首先,将现有的数组a进行排序,最大值就是让y个人全部坐在目前人最多的那个长椅上,即mx=a[n-1]+y。
然后最小值就是要让每个长椅上的人尽可能地均匀,有两种情况:
(1)当y不足以分配给其他长椅使他们的数值都达到a[n-1]时,那么最小值就是a[n-1];
(2)当y足以分配给其他长椅使他们的数值都达到a[n-1]时,先分配,即让所有的长椅的人数都达到k,然后剩下的人平均分给x个长椅,然后最多的那个即为mn.
最后依次输出mn和mx即可。
3.代码:
#includeWeek10作业
A-签到题
1.题意:东东在玩游戏“Game23”。
在一开始他有一个数字n,他的目标是把它转换成m,在每一步操作中,他可以将n乘以2或乘以3,他可以进行任意次操作。输出将n转换成m的操作次数,如果转换不了输出-1。
Input
输入的唯一一行包括两个整数n和m(1<=n<=m<=5*10^8).
Output
输出从n转换到m的操作次数,否则输出-1.
2.题意:该问题较为简单,由题意知,转换时只能乘以2或3,故转换过程有且只有一组解。所以我们只需使用两个while循环便可求出答案。
3.代码:
#include B-LIS&LCS
1.题意:东东有两个序列A和B。
他想要知道序列A的LIS和序列AB的LCS的长度。
注意,LIS为严格递增的,即a1
Input
第一行两个数n,m(1<=n<=5,000,1<=m<=5,000)
第二行n个数,表示序列A
第三行m个数,表示序列B
Output
输出一行数据ans1和ans2,分别代表序列A的LIS和序列AB的LCS的长度
2.思路:
一、
对于数组A,求解LIS的过程如下:
定义 fi 表示以 Ai 为结尾的最长上升序列的方程。
初始化时f1 = 1,转移过程如下:
![]()
LIS的长度为max{f[i], i=1…n }
此外也可以调用LCS函数来计算LIS,求出A数组和按升序排列的A数组的LCS
长度即可。
注:因为要求解的LIS为严格递增的,所以A数组排完序后需要将重复的元素覆盖掉。
二、
对于数组a, b,求解LCS 的过程如下(A的size为m, B的size为n)。
假设f[i][j] 为 a1, a2, …, ai 和 b1, b2, …, bj 的 LCS 长度
初始时f[1][0] = f[0][1] = f[0][0] = 0
当 ai == bj 时,f[i][j] = f[i-1][j-1] + 1,否则 f[i][j] = max(f[i-1][j], f[i][j-1])
然后f[m][n]的值即为LCS 的长度。
3.代码:
#include C-拿数问题
1.题意:YJQ 上完第10周的程序设计思维与实践后,想到一个绝妙的主意,他对拿数问题做了一点小修改,使得这道题变成了 拿数问题 II。
给一个序列,里边有 n 个数,每一步能拿走一个数,比如拿第 i 个数, Ai = x,得到相应的分数 x,但拿掉这个 Ai 后,x+1 和 x-1 (如果有 Aj = x+1 或 Aj = x-1 存在) 就会变得不可拿(但是有 Aj = x 的话可以继续拿这个 x)。求最大分数。
Input
第一行包含一个整数 n (1 ≤ n ≤ 105),表示数字里的元素的个数
第二行包含n个整数a1, a2, …, an (1 ≤ ai ≤ 105)
Output
输出一个整数:n你能得到最大分值。
2.思路:本题与上课所讲主要是存储方式不同,对于数值x,数组a中a[x]为其出现的次数。max为x中的最大值,之后计算过程与上课讲的类似。
dp[i] , 仅考虑 A[1…i] ,能拿到的最大分数
初始时dp[0] = 0, dp[1] = a[1].
dp[i] = max(dp[i-1], dp[i-2]+a[i]*i);
然后输出dp[max1]即可。
同时因1 ≤ n ≤ 100000和1 ≤ ai ≤ 100000,故最终结果用long long int来表示。
3.代码:
#include 月模拟题3-炉石传说
1.题意:《炉石传说:魔兽英雄传》(Hearthstone: Heroes of Warcraft,简称炉石传说)是暴雪娱乐开发的一款集换式卡牌游戏(如下图所示)。

游戏在一个战斗棋盘上进行,由两名玩家轮流进行操作,本题所使用的炉石传说游戏的简化规则如下:
* 玩家会控制一些角色,每个角色有自己的生命值和攻击力。当生命值小于等于 0 时,该角色死亡。角色分为英雄和随从。
* 玩家各控制一个英雄,游戏开始时,英雄的生命值为 30,攻击力为 0。当英雄死亡时,游戏结束,英雄未死亡的一方获胜。
* 玩家可在游戏过程中召唤随从。棋盘上每方都有 7 个可用于放置随从的空位,从左到右一字排开,被称为战场。当随从死亡时,它将被从战场上移除。
* 游戏开始后,两位玩家轮流进行操作,每个玩家的连续一组操作称为一个回合。
* 每个回合中,当前玩家可进行零个或者多个以下操作:
1) 召唤随从:玩家召唤一个随从进入战场,随从具有指定的生命值和攻击力。
2) 随从攻击:玩家控制自己的某个随从攻击对手的英雄或者某个随从。
3) 结束回合:玩家声明自己的当前回合结束,游戏将进入对手的回合。该操作一定是一个回合的最后一个操作。
* 当随从攻击时,攻击方和被攻击方会同时对彼此造成等同于自己攻击力的伤害。受到伤害的角色的生命值将会减少,数值等同于受到的伤害。例如,随从 X 的生命值为 HX、攻击力为 AX,随从 Y 的生命值为 HY、攻击力为 AY,如果随从 X 攻击随从 Y,则攻击发生后随从 X 的生命值变为 HX - AY,随从 Y 的生命值变为 HY - AX。攻击发生后,角色的生命值可以为负数。
本题将给出一个游戏的过程,要求编写程序模拟该游戏过程并输出最后的局面。
Input
输入第一行是一个整数 n,表示操作的个数。接下来 n 行,每行描述一个操作,格式如下:
…
其中表示操作类型,是一个字符串,共有 3 种:summon表示召唤随从,attack表示随从攻击,end表示结束回合。这 3 种操作的具体格式如下:
* summon :当前玩家在位置召唤一个生命值为、攻击力为的随从。其中是一个 1 到 7 的整数,表示召唤的随从出现在战场上的位置,原来该位置及右边的随从都将顺次向右移动一位。
* attack :当前玩家的角色攻击对方的角色 。是 1 到 7 的整数,表示发起攻击的本方随从编号,是 0 到 7 的整数,表示被攻击的对方角色,0 表示攻击对方英雄,1 到 7 表示攻击对方随从的编号。
* end:当前玩家结束本回合。
注意:随从的编号会随着游戏的进程发生变化,当召唤一个随从时,玩家指定召唤该随从放入战场的位置,此时,原来该位置及右边的所有随从编号都会增加 1。而当一个随从死亡时,它右边的所有随从编号都会减少 1。任意时刻,战场上的随从总是从1开始连续编号。
数据规模:
* 操作的个数0 ≤ n ≤ 1000。
* 随从的初始生命值为 1 到 100 的整数,攻击力为 0 到 100 的整数。
* 保证所有操作均合法,包括但不限于:
1) 召唤随从的位置一定是合法的,即如果当前本方战场上有 m 个随从,则召唤随从的位置一定在 1 到 m + 1 之间,其中 1 表示战场最左边的位置,m + 1 表示战场最右边的位置。
2) 当本方战场有 7 个随从时,不会再召唤新的随从。
3) 发起攻击和被攻击的角色一定存在,发起攻击的角色攻击力大于 0。
4) 一方英雄如果死亡,就不再会有后续操作。
数据约定:
前 20% 的评测用例召唤随从的位置都是战场的最右边。
前 40% 的评测用例没有 attack 操作。
前 60% 的评测用例不会出现随从死亡的情况。
Output
输出共 5 行:
第 1 行包含一个整数,表示这 n 次操作后(以下称为 T 时刻)游戏的胜负结果,1 表示先手玩家获胜,-1 表示后手玩家获胜,0 表示游戏尚未结束,还没有人获胜。
第 2 行包含一个整数,表示 T 时刻先手玩家的英雄的生命值。
第 3 行包含若干个整数,第一个整数 p 表示 T 时刻先手玩家在战场上存活的随从个数,之后 p 个整数,分别表示这些随从在 T 时刻的生命值(按照从左往右的顺序)。
第 4 行和第 5 行与第 2 行和第 3 行类似,只是将玩家从先手玩家换为后手玩家。
Example
Input
8
summon 1 3 6
summon 2 4 2
end
summon 1 4 5
summon 1 2 1
attack 1 2
end
attack 1 1
12345678910
Output
0
30
1 2
30
1 2
2.思路:首先构建一个结构体,用于存储英雄和随从的攻击力和血量。利用vector数组分别存储先手和后手玩家,a[0]为先手玩家,a[1]为后手玩家。先手和后手的交换可以通过(m+1)%2或!m实现。
直接调用vector数组完成数据的插入和删除。需要注意的就是当一方英雄血量<=0时,不需要删除元素,还有就是输出的血量可能为负数。
3.代码:
#include 月模拟题4-元素模拟器
1.题意:


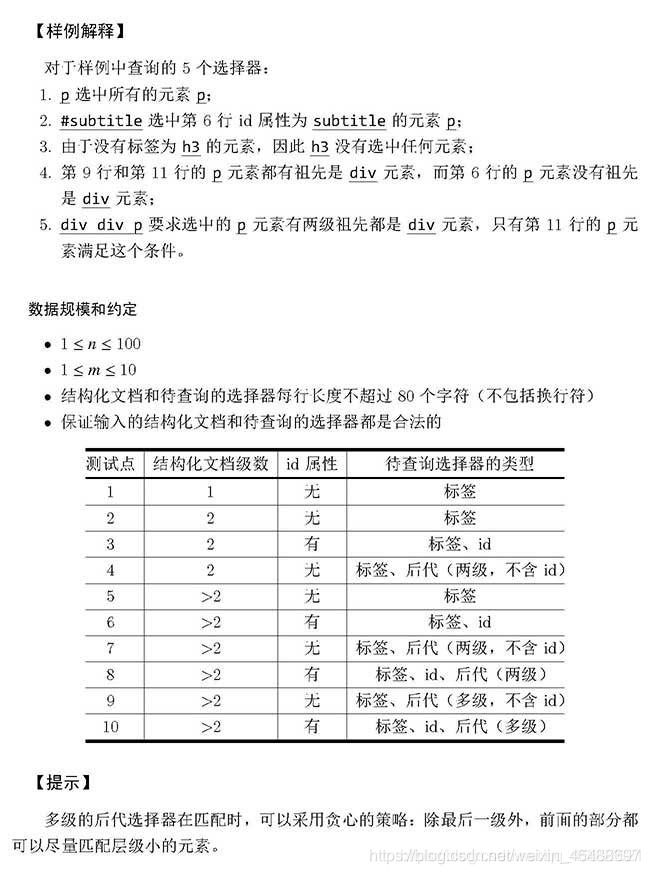
2.思路:定义元素结构体element,内含标签、id、行数、级数四个属性。
文档读入时,判断其标签属性,并使用transform函数并将其全部转为小写,id属性不变,同时还要记录其行号和级数,将其存放于element类型的一个数组的中,其索引即为元素下标。
读入元素选择器,利用vector存储。
有空格则间断,标签属性全部转为小写。然后对vector中内容进行逐步查找,在查找过程中,记录下一步查找的起始行和最小级。如果是查找的最后一步,即vector中的最后一个元素,则查找到元素相等且级数大于最小级的元素存入vector中即可,即为答案。如果不是,则使用提示的贪心策略,找到层级最小的匹配项。
3.代码:
#include Week14-猫睡觉问题
1.题意:众所周知,TT家里有一只魔法喵。这只喵十分嗜睡。一睡就没有白天黑夜。喵喵一天可以睡多次!!每次想睡多久就睡多久╭(╯^╰)╮
喵睡觉的时段是连续的,即一旦喵喵开始睡觉了,就不能被打扰,不然喵会咬人哒[○・`Д´・ ○]
可以假设喵喵必须要睡眠连续不少于 A 个小时,即一旦喵喵开始睡觉了,至少连续 A 个小时内(即A*60分钟内)不能被打扰!
现在你知道喵喵很嗜睡了,它一天的时长都在吃、喝、拉、撒、睡,换句话说要么睡要么醒着滴!
众所周知,这只魔法喵很懒,和TT一样懒,它不能连续活动超过 B 个小时。
猫主子是不用工作不用写代码滴,十分舒适,所以,它是想睡就睡滴。
但是,现在猫主子有一件感兴趣的事,就是上BiliBili网站看的新番。
新番的播放时间它已经贴在床头啦(每天都用同一张时间表哦),这段时间它必须醒着!!
作为一只喵喵,它认为安排时间是很麻烦的事情,现在请你帮它安排睡觉的时间段。
Input
多组数据,多组数据,多组数据哦,每组数据的格式如下:
第1行输入三个整数,A 和 B 和 N (1 <= A <= 24, 1 <= B <= 24, 1 <= n <= 20)
第2到N+1行为每日的新番时间表,每行一个时间段,格式形如 hh:mm-hh:mm (闭区间),这是一种时间格式,hh:mm 的范围为 00:00 到 23:59。注意一下,时间段是保证不重叠的,但是可能出现跨夜的新番,即新番的开始时间点大于结束时间点。
保证每个时间段的开始时间点和结束时间点不一样,即不可能出现类似 08:00-08:00 这种的时间段。时长的计算由于是闭区间所以也是有点坑的,比如 12:00-13:59 的时长就是 120 分钟。
不保证输入的新番时间表有序。
Output
我们知道,时间管理是一项很难的活,所以你可能没有办法安排的那么好,使得这个时间段满足喵喵的要求,即每次睡必须时间连续且不少于 A 小时,每次醒必须时间连续且不大于 B 小时,还要能看完所有的番,所以输出的第一行是 Yes 或者 No,代表是否存在满足猫猫要求的时间管理办法。
然后,对于时间管理,你只要告诉喵喵,它什么时候睡觉即可。
即第2行输出一个整数 k,代表当天有多少个时间段要睡觉
接下来 k 行是喵喵的睡觉时间段,每行一个时间段,格式形如 hh:mm-hh:mm (闭区间),这个在前面也有定义。注意一下,如果喵喵的睡眠时段跨越当天到达了明天,比如从23点50分睡到0点40分,那就输出23:50-00:40,如果从今晚23:50睡到明天早上7:30,那就输出23:50-07:30。
输出要排序吗?(输出打乱是能过的,也就是说,题目对输出的那些时间段间的顺序是没有要求的)
哦对了,喵喵告诉你说,本题是 Special Judge,如果你的输出答案和 Sample 不太一样,也可能是对的,它有一个判题程序来判定你的答案(当然,你对你自己的答案肯定也能肉眼判断)
Sample Input
12 12 1
23:00-01:00
3 4 3
07:00-08:00
11:00-11:09
19:00-19:59
Sample Output
Yes
1
01:07-22:13
No
2.思路:这个题目简单来说就是个区间检查问题,首先依次输入多个区间,然后我们再查看各个新生成的区间和原区间的情况,输出满足条件的区间。区间的输入好解决,输入之后按照时间大小先后排序即可。唯一需要注意的地方就是这应该是一个环,所以我直接将最小的时间点插入到排好序的数组中。
接下来就是检查各个区间的情况,在输入时,我将区间的起点记为1,终点记为0。所以我们每一次遍历都需要从值为1的结点开始。然后检查区间的时长,如果时长大于所允许的最大值,那么就说明无法完成编排;
还有就是清醒区间时长的计算可能不止一个区间,有可能是多个区间的和,因此我们每一次统计都需要统计到第一个可以睡觉的区间(一旦遇到,将之前的统计结果清零即可)。除此之外,就是需要注意环的问题,遍历到结尾时有可能要回到开头的。
3.代码:
#include Week10-东东转魔方
1.题意:东东有一个二阶魔方,即2×2×2的一个立方体组。立方体由八个角组成。
魔方的每一块都用三维坐标(h, k, l)标记,其中h, k, l∈{0,1}。六个面的每一个都有四个小面,每个小面都有一个正整数。
对于每一步,东东可以选择一个特定的面,并把此面顺时针或逆时针转90度。
请你判断,是否东东可以在一个步骤还原这个魔方(每个面没有异色)。
Input
输入的第一行包含一个整数N(N≤30),这是测试用例的数量。
对于每个测试用例, 第 1~4 个数描述魔方的顶面,这是常见的2×2面,由(0,0,1),(0,1,1),(1,0,1),(1,1,1)标记。四个整数对应于上述部分。
第 5~8 个数描述前面,即(1,0,1),(1,1,1),(1,0,0),(1,1,0)的公共面。四个整数 与上述各部分相对应。
第 9~12 个数描述底面,即(1,0,0),(1,1,0),(0,0,0),(0,1,0)的公共面。四个整数与上述各部分相对应。
第 13~16 个数描述背面,即(0,0,0),(0,1,0),(0,0,1),(0,1),(0,1,1)的公共面。四个整数与上述各部分相对应。
第 17~20 个数描述左面,即(0,0,0),(0,0,1),(1,0,0),(1,0,1)的公共面。给出四个整数与上述各部分相对应。
第 21~24 个数描述了右面,即(0,1,1),(0,1,0),(1,1,1),(1,1,0)的公共面。给出四个整数与上述各部分相对应。
换句话说,每个测试用例包含24个整数a、b、c到x。你可以展开表面以获得平面图
Output
对于每个测试用例,魔方如果可以至多 “只转一步” 恢复,输出YES,则输出NO。
2.思路:本题需要在开始考虑好解题框架,否则会带来一些不必要的麻烦。由题意知,本题的魔方是一个二阶,即222的立方体组,故转的方法有:上面顺时针转90度,前面顺时针,前面逆时针,左边顺时针(相当于右边顺时针),左边逆时针(相当于左边逆时针),逆时针转,分别对不同的情况进行处理,最后按要求输出结果即可。
3.代码:
#include