深度强化学习(DRL)三:从Q-learning到Deep Q Network(DQN)
目录
- 一、Q-learning
- 二、Deep Q Network
- 三、Double DQN
一、Q-learning
关于Q-learning,网上的资料很多,简单的总结一下它的特点。
Q-learning最核心的是有一个Q表,它记录了在环境中的 所有状态(s) 以及每个状态可以进行的 所有行为(a) 的Q值,初值设为0。
| 状态 \ 行为 | a1 | a2 | a3 | a4 |
|---|---|---|---|---|
| s1 | ||||
| s2 | ||||
| s3 | ||||
| …… |
Q值的更新公式如下:
Q ( s , a ) ← Q ( s , a ) + α [ r + γ m a x a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)←Q(s,a)+α[r+\gamma max_{a'}Q(s^′,a^′)−Q(s,a)] Q(s,a)←Q(s,a)+α[r+γmaxa′Q(s′,a′)−Q(s,a)]
- 其中 α α α表示学习速率,取值小于1
- r r r是设置的奖励
- 智能体在状态s经过行为a转移到状态s’, m a x a ′ Q ( s ′ , a ′ ) max_{a'}Q(s^′,a^′) maxa′Q(s′,a′) 是状态 s ′ s' s′ 那一行最大Q值
- γ \gamma γ则是衰减速率,取值在0到1之间, γ \gamma γ越大,智能体就会越注重长期利益, γ \gamma γ越小,智能体越短视。
每改变一次状态就会更新一次Q值
Q-learning 是一个 off-policy 的算法,它可以离线学习。它可以随机进行若干次游戏,将游戏过程保存起来,学习的时候就可以避免陷入局部最优。
Q-learning 的代码实现:
# -*- coding: UTF-8 -*-
import numpy as np
import pandas as pd
class QLearningTable:
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
self.actions = actions # a list
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon = e_greedy
self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)
def choose_action(self, observation):
self.check_state_exist(observation)
# action selection
if np.random.uniform() < self.epsilon:
# choose best action
state_action = self.q_table.loc[observation, :]
state_action = state_action.reindex(np.random.permutation(state_action.index)) # some actions have same value
action = state_action.idxmax()
else:
# choose random action
action = np.random.choice(self.actions)
return action
def learn(self, s, a, r, s_):
self.check_state_exist(s_)
q_predict = self.q_table.loc[s, a]
if s_ != 'terminal':
q_target = r + self.gamma * self.q_table.loc[s_, :].max() # next state is not terminal
else:
q_target = r # next state is terminal
self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # update
def check_state_exist(self, state):
if state not in self.q_table.index:
# append new state to q table
self.q_table = self.q_table.append(
pd.Series(
[0]*len(self.actions),
index=self.q_table.columns,
name=state,
)
)
二、Deep Q Network
如果想用Q-learning玩之前的CartPole-v0游戏,会发现CartPole-v0的状态值太多了,它的observation有 车的位置,车的速度,杆子的角度,杆子顶端的速度 四个值,并且是连续的数值,四个值再进行量化,Q表实在是太大了。用Q-learning玩游戏和随机玩游戏没区别,学习不到东西。可能Q-learning只适用于走迷宫类的游戏,每一步的状态都可以很简单的描述出来,4*4的迷宫只需要用16个状态就可以全部囊括。
我们用Deep Q Network来解决这个问题, Deep Q Network融合了神经网络和 Q learning。
- 我们可以将状态和动作当成神经网络的输入, 然后经过神经网络分析后得到动作的 Q 值, 这样我们就没必要在表格中记录 Q 值, 而是直接使用神经网络生成 Q 值.
- 或者只输入状态值, 输出所有的动作值, 然后按照 Q learning 的原则, 直接选择拥有最大值的动作当做下一步要做的动作.

需要搭建两个神经网络,target_net 和 eval_net ,
target_net 用于预测 q_target 值, 他不会及时更新参数.
target_net 用于预测 q_eval, 这个神经网络拥有最新的神经网络参数.
两个神经网络结构是完全一样的, 只是里面的参数不一样. target_net 是 eval_net 的一个历史版本, 拥有 eval_net 很久之前的一组参数, 而且这组参数被固定一段时间, 然后再被 eval_net 的新参数所替换. 而 eval_net 是不断在被提升的。这样做是为了打乱数据间的相关性,避免陷入局部最优。
神经网络的输入数据是[s,a,r,s’],输出数据是状态s下所有行为a的Q值。
target_net 只会输出Q值(q_target ),不会进行训练,而eval_net 输出Q值(q_eval)之后会根据q_target和q_eval进行反向传播训练,更新eval_net 的参数。
Deep Q Network整个算法的运作:
- 初始化target_net 和 target_net。
- 观察游戏状态observation,选择合适的observation作为输入,一般情况会对observation做数据处理,使其更容易训练,这里不用。
- 设置合适的奖励reward。
- 先进行若干次游戏,将游戏数据存储到memory中。
- 从memory中随机选取训练数据batch_memory用于批量训练。
- 训练eval_net 一段时间后,将eval_net 的参数复制给target_net 。
- 训练过程中产生的新的游戏数据会替代memory中的旧数据。
回到游戏CartPole-v0
DQN.py:
import numpy as np
import tensorflow as tf
np.random.seed(1)
tf.set_random_seed(1)
# Deep Q Network off-policy
class DeepQNetwork:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=300,
memory_size=500,
batch_size=32,
e_greedy_increment=None,
output_graph=True,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = e_greedy
self.replace_target_iter = replace_target_iter
self.memory_size = memory_size
self.batch_size = batch_size
self.epsilon_increment = e_greedy_increment
self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max
# total learning step
self.learn_step_counter = 0
# initialize zero memory [s, a, r, s_]
# [4, 1, 1, 4]
self.memory = np.zeros((self.memory_size, n_features * 2 + 2))
# consist of [target_net, evaluate_net]
self._build_net()
t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='target_net')
e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='eval_net')
with tf.variable_scope('hard_replacement'):
self.target_replace_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
self.sess = tf.Session()
if output_graph:
# $ tensorboard --logdir=logs
tf.summary.FileWriter("logs/", self.sess.graph)
self.sess.run(tf.global_variables_initializer())
self.cost_his = []
def _build_net(self):
# ------------------ all inputs ------------------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # input State
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # input Next State
self.r = tf.placeholder(tf.float32, [None, ], name='r') # input Reward
self.a = tf.placeholder(tf.int32, [None, ], name='a') # input Action
w_initializer, b_initializer = tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1)
# ------------------ build evaluate_net ------------------
with tf.variable_scope('eval_net'):
e1 = tf.layers.dense(self.s, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='e1')
self.q_eval = tf.layers.dense(e1, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='q')
# ------------------ build target_net ------------------
with tf.variable_scope('target_net'):
t1 = tf.layers.dense(self.s_, 20, tf.nn.relu, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='t1')
self.q_next = tf.layers.dense(t1, self.n_actions, kernel_initializer=w_initializer,
bias_initializer=b_initializer, name='t2')
with tf.variable_scope('q_target'):
q_target = self.r + self.gamma * tf.reduce_max(self.q_next, axis=1, name='Qmax_s_') # shape=(None, )
self.q_target = tf.stop_gradient(q_target)
with tf.variable_scope('q_eval'):
a_indices = tf.stack([tf.range(tf.shape(self.a)[0], dtype=tf.int32), self.a], axis=1)
self.q_eval_wrt_a = tf.gather_nd(params=self.q_eval, indices=a_indices) # shape=(None, )
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval_wrt_a, name='TD_error'))
with tf.variable_scope('train'):
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
def store_transition(self, s, a, r, s_):
if not hasattr(self, 'memory_counter'):
self.memory_counter = 0
transition = np.hstack((s, [a, r], s_))
# replace the old memory with new memory
index = self.memory_counter % self.memory_size
self.memory[index, :] = transition
self.memory_counter += 1
def choose_action(self, observation):
# to have batch dimension when feed into tf placeholder
observation = observation[np.newaxis, :]
if np.random.uniform() < self.epsilon:
# forward feed the observation and get q value for every actions
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value)
else:
action = np.random.randint(0, self.n_actions)
return action
def learn(self):
# check to replace target parameters
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.target_replace_op)
print('\ntarget_params_replaced\n')
# sample batch memory from all memory
if self.memory_counter > self.memory_size:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
else:
sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
_, cost = self.sess.run(
[self._train_op, self.loss],
feed_dict={
self.s: batch_memory[:, :self.n_features],
self.a: batch_memory[:, self.n_features],
self.r: batch_memory[:, self.n_features + 1],
self.s_: batch_memory[:, -self.n_features:],
})
self.cost_his.append(cost)
# increasing epsilon
self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
self.learn_step_counter += 1
def plot_cost(self):
import matplotlib.pyplot as plt
plt.plot(np.arange(len(self.cost_his)), self.cost_his)
plt.ylabel('Cost')
plt.xlabel('training steps')
plt.show()
if __name__ == '__main__':
DQN = DeepQNetwork(3, 4, output_graph=True)
DQN_CarPole.py:
import gym
from DQN import DeepQNetwork
env = gym.make('CartPole-v0')
env = env.unwrapped
RL = DeepQNetwork(n_actions=env.action_space.n,
n_features=env.observation_space.shape[0],
learning_rate=0.01, e_greedy=0.9,
replace_target_iter=100, memory_size=2000,
e_greedy_increment=0.0008, )
total_steps = 0 # 记录步数
for i_episode in range(100):
# 获取回合 i_episode 第一个 observation
observation = env.reset()
ep_r = 0
while True:
env.render() # 刷新环境
action = RL.choose_action(observation) # 选行为
observation_, reward, done, info = env.step(action) # 获取下一个 state
x, x_dot, theta, theta_dot = observation_ # 细分开, 为了修改原配的 reward
# x 是车的水平位移, 所以 r1 是车越偏离中心, 分越少
# theta 是棒子离垂直的角度, 角度越大, 越不垂直. 所以 r2 是棒越垂直, 分越高
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
reward = r1 + r2 # 总 reward 是 r1 和 r2 的结合, 既考虑位置, 也考虑角度, 这样 DQN 学习更有效率
# 保存这一组记忆
RL.store_transition(observation, action, reward, observation_)
if total_steps > 1000:
RL.learn() # 学习
ep_r += reward
if done:
print('episode: ', i_episode,
'ep_r: ', round(ep_r, 2),
' epsilon: ', round(RL.epsilon, 2))
break
observation = observation_
total_steps += 1
# 最后输出 cost 曲线
RL.plot_cost()
env.close()
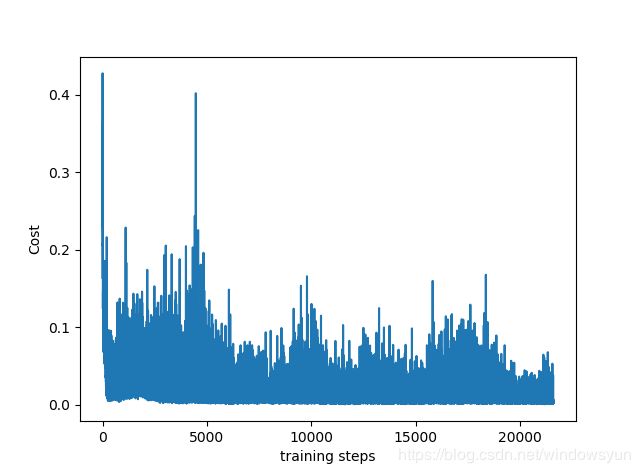
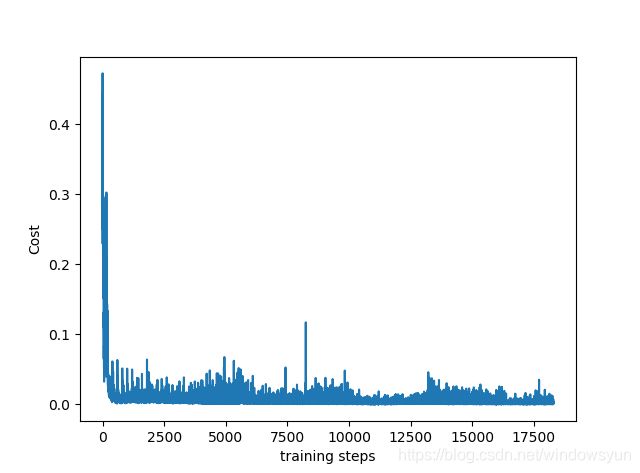
运行DQN_CarPole.py
发现小车确实变得越来越稳定。
三、Double DQN
无论是Q-learning还是DQN,更新Q值的的时候都会用到 m a x Q maxQ maxQ。
Q-learning:
Q ( s , a ) ← Q ( s , a ) + α [ r + γ m a x a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)←Q(s,a)+α[r+\gamma max_{a'}Q(s^′,a^′)−Q(s,a)] Q(s,a)←Q(s,a)+α[r+γmaxa′Q(s′,a′)−Q(s,a)]
使用max虽然可以快速让Q值向可能的优化目标靠拢,但是很容易过犹不及,导致过度估计(Over Estimation),所谓过度估计就是最终我们得到的算法模型有很大的偏差(bias),可能就会发现Q值都超级大。
DDQN通过解耦目标Q值动作的选择和目标Q值的计算这两步,来达到消除过度估计的问题。
在DDQN这里,不再是直接在目标Q网络里面找各个动作中最大Q值,而是先在当前Q网络中先找出最大Q值对应的动作。然后利用这个选择出来的动作在目标Q网络里面去计算目标Q值。
DoubleDQN.py
import numpy as np
import tensorflow as tf
np.random.seed(1)
tf.set_random_seed(1)
class DoubleDQN:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.005,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=200,
memory_size=3000,
batch_size=32,
e_greedy_increment=None,
output_graph=False,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = e_greedy
self.replace_target_iter = replace_target_iter
self.memory_size = memory_size
self.batch_size = batch_size
self.epsilon_increment = e_greedy_increment
self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max
self.learn_step_counter = 0
self.memory = np.zeros((self.memory_size, n_features * 2 + 2))
self._build_net()
t_params = tf.get_collection('target_net_params')
e_params = tf.get_collection('eval_net_params')
self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
self.sess = tf.Session()
if output_graph:
tf.summary.FileWriter("logs/", self.sess.graph)
self.sess.run(tf.global_variables_initializer())
self.cost_his = []
def _build_net(self):
def build_layers(s, c_names, n_l1, w_initializer, b_initializer):
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(s, w1) + b1)
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
out = tf.matmul(l1, w2) + b2
return out
# ------------------ build evaluate_net ------------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # input
self.q_target = tf.placeholder(tf.float32, [None, self.n_actions], name='Q_target') # for calculating loss
with tf.variable_scope('eval_net'):
c_names, n_l1, w_initializer, b_initializer = \
['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 20, \
tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1) # config of layers
self.q_eval = build_layers(self.s, c_names, n_l1, w_initializer, b_initializer)
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
with tf.variable_scope('train'):
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
# ------------------ build target_net ------------------
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # input
with tf.variable_scope('target_net'):
c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
self.q_next = build_layers(self.s_, c_names, n_l1, w_initializer, b_initializer)
def store_transition(self, s, a, r, s_):
if not hasattr(self, 'memory_counter'):
self.memory_counter = 0
transition = np.hstack((s, [a, r], s_))
index = self.memory_counter % self.memory_size
self.memory[index, :] = transition
self.memory_counter += 1
def choose_action(self, observation):
observation = observation[np.newaxis, :]
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value)
if not hasattr(self, 'q'): # record action value it gets
self.q = []
self.running_q = 0
self.running_q = self.running_q * 0.99 + 0.01 * np.max(actions_value)
self.q.append(self.running_q)
if np.random.uniform() > self.epsilon: # choosing action
action = np.random.randint(0, self.n_actions)
return action
def learn(self):
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.replace_target_op)
print('\ntarget_params_replaced\n')
if self.memory_counter > self.memory_size:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
else:
sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
q_next, q_eval4next = self.sess.run(
[self.q_next, self.q_eval],
feed_dict={self.s_: batch_memory[:, -self.n_features:], # next observation
self.s: batch_memory[:, -self.n_features:]}) # next observation
q_eval = self.sess.run(self.q_eval, {self.s: batch_memory[:, :self.n_features]})
q_target = q_eval.copy()
batch_index = np.arange(self.batch_size, dtype=np.int32)
eval_act_index = batch_memory[:, self.n_features].astype(int)
reward = batch_memory[:, self.n_features + 1]
max_act4next = np.argmax(q_eval4next,
axis=1) # the action that brings the highest value is evaluated by q_eval
selected_q_next = q_next[batch_index, max_act4next] # Double DQN, select q_next depending on above actions
q_target[batch_index, eval_act_index] = reward + self.gamma * selected_q_next
_, self.cost = self.sess.run([self._train_op, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features],
self.q_target: q_target})
self.cost_his.append(self.cost)
self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
self.learn_step_counter += 1
def plot_cost(self):
import matplotlib.pyplot as plt
plt.plot(np.arange(len(self.cost_his)), self.cost_his)
plt.ylabel('Cost')
plt.xlabel('training steps')
plt.show()
DoubleDQN_CarPole.py
import tensorflow as tf
import gym
from DoubleDQN import DoubleDQN
env = gym.make('CartPole-v0')
env = env.unwrapped
double_DQN = DoubleDQN(n_actions=env.action_space.n,
n_features=env.observation_space.shape[0],
memory_size=2000,
e_greedy_increment=0.001,
output_graph=True)
total_steps = 0 # 记录步数
for i_episode in range(100):
# 获取回合 i_episode 第一个 observation
observation = env.reset()
ep_r = 0
while True:
env.render() # 刷新环境
action = double_DQN.choose_action(observation) # 选行为
observation_, reward, done, info = env.step(action) # 获取下一个 state
x, x_dot, theta, theta_dot = observation_ # 细分开, 为了修改原配的 reward
# x 是车的水平位移, 所以 r1 是车越偏离中心, 分越少
# theta 是棒子离垂直的角度, 角度越大, 越不垂直. 所以 r2 是棒越垂直, 分越高
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
reward = r1 + r2 # 总 reward 是 r1 和 r2 的结合, 既考虑位置, 也考虑角度, 这样 DQN 学习更有效率
# 保存这一组记忆
double_DQN.store_transition(observation, action, reward, observation_)
if total_steps > 1000:
double_DQN.learn() # 学习
ep_r += reward
if done:
print('episode: ', i_episode,
'ep_r: ', round(ep_r, 2),
' epsilon: ', round(double_DQN.epsilon, 2))
break
observation = observation_
total_steps += 1
# 最后输出 cost 曲线
double_DQN.plot_cost()
env.close()