1.4 矩阵方程(第1章 线性代数中的线性方程组)
内容概述
本节引入了矩阵方程的概念,并指出了矩阵方程、向量方程、线性方程组之间的等价关系,这种等价关系可以指导我们在解决现实问题时根据不同的情况灵活运用。接着,讲了矩阵方程 A x = b A\boldsymbol x =\boldsymbol b Ax=b的一些基本性质,例如解的存在性, A x A\boldsymbol x Ax如何计算,以及 A x A\boldsymbol x Ax这一矩阵-向量积的运算法则。
矩阵方程及其与向量方程、线性方程组的关系
线性代数中的一个基本思想是把向量的线性组合看作矩阵与向量的积。
定义:
若 A A A是 m × n m \times n m×n矩阵,它的各列为 a 1 , ⋯ , a n \boldsymbol a_1, \boldsymbol \cdots, \boldsymbol a_n a1,⋯,an。若 x \boldsymbol x x是 R n \mathbb R^n Rn中的向量,则 A A A与 x \boldsymbol x x的积(记为 A x A\boldsymbol x Ax)就是 A A A的各列以 x \boldsymbol x x中对应元素为权的线性组合,即:
A x = [ a 1 a 2 ⋯ a n ] [ x 1 x 2 ⋯ x n ] = x 1 a 1 + x 2 a 2 + ⋯ + x n a n A\boldsymbol x=[\boldsymbol a_1\quad \boldsymbol a_2 \quad\cdots \quad\boldsymbol a_n] \begin{bmatrix}x_1 \\ x_2 \\ \cdots \\ x_n\end{bmatrix}=x_1\boldsymbol a_1 + x_2\boldsymbol a_2 + \cdots + x_n\boldsymbol a_n Ax=[a1a2⋯an]⎣⎢⎢⎡x1x2⋯xn⎦⎥⎥⎤=x1a1+x2a2+⋯+xnan
注意 A x A\boldsymbol x Ax仅当 A A A的列数等于 x x x中的元素个数时才有定义。
例:
对 R m \mathbb R^m Rm中的 v 1 \boldsymbol v_1 v1, v 2 \boldsymbol v_2 v2, v 3 \boldsymbol v_3 v3,把线性组合 3 v 1 − 5 v 2 + 7 v 3 3\boldsymbol v_1 - 5\boldsymbol v_2 + 7\boldsymbol v_3 3v1−5v2+7v3表示为矩阵乘向量的形式。
解:
根据上述定义,可以把 v 1 \boldsymbol v1 v1, v 2 \boldsymbol v2 v2, v 3 \boldsymbol v3 v3排列成矩阵 A A A,把数 3 3 3, − 5 -5 −5, 7 7 7排列成向量 x \boldsymbol x x,即:
3 v 1 − 5 v 2 + 7 v 3 = [ v 1 v 2 v 3 ] [ 3 − 5 7 ] 3\boldsymbol v_1 - 5\boldsymbol v_2 + 7\boldsymbol v_3 = [\boldsymbol v_1\quad \boldsymbol v_2\quad \boldsymbol v_3]\begin{bmatrix}3 \\ -5 \\ 7\end{bmatrix} 3v1−5v2+7v3=[v1v2v3]⎣⎡3−57⎦⎤
现在可以梳理一下,如何把线性方程组、线性组合、向量方程、矩阵方程的概念统一起来:
例:
有如下方程组:
x 1 + 2 x 2 − x 3 = 4 − 5 x 2 + 3 x 3 = 1 \begin{aligned} x_1 + 2x_2 - x_3 = 4\\ -5x_2 + 3x_3 =1 \end{aligned} x1+2x2−x3=4−5x2+3x3=1
等价于下列的向量方程:
x 1 [ 1 0 ] + x 2 [ 2 − 5 ] + x 3 [ − 1 3 ] = [ 4 1 ] x_1\begin{bmatrix}1 \\ 0\end{bmatrix} + x_2\begin{bmatrix}2 \\ -5\end{bmatrix} + x_3\begin{bmatrix}-1 \\ 3\end{bmatrix} =\begin{bmatrix}4 \\ 1\end{bmatrix} x1[10]+x2[2−5]+x3[−13]=[41]
也等价于下列的矩阵方程:
[ 1 2 − 1 0 − 5 3 ] [ x 1 x 2 x 3 ] = [ 4 1 ] \begin{bmatrix}1 & 2 & -1 \\ 0 & -5 & 3\end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}4 \\ 1\end{bmatrix} [102−5−13]⎣⎡x1x2x3⎦⎤=[41]
也就是说,任何线性方程组或向量方程都可以写成等价的形式为 A x = b A\boldsymbol x = \boldsymbol b Ax=b的矩阵方程,这个概念在线性代数中十分重要。
下列用数学语言描述这一事实:
定理:
若 A A A是 m × n m \times n m×n矩阵,它的各列为 a 1 , ⋯ , a n a_1, \cdots, a_n a1,⋯,an,而 b b b属于 R m \mathbb R^m Rm,则矩阵方程:
A x = b A\boldsymbol x = \boldsymbol b Ax=b
与向量方程:
x 1 a 1 + x 2 a n + ⋯ + x n a n = b x_1\boldsymbol a_1 + x_2\boldsymbol a_n + \cdots + x_n\boldsymbol a_n = b x1a1+x2an+⋯+xnan=b
有相同的解集。它又与增广矩阵为
[ a 1 a 2 ⋯ a n b ] [\boldsymbol a_1 \quad \boldsymbol a_2 \quad \cdots \quad \boldsymbol a_n \quad \boldsymbol b] [a1a2⋯anb]
的线性方程组有相同的解集
上述定理给出了研究线性代数问题的一个有力工具,使我们可将线性方程组用三种不同但彼此等价的观点来研究:作为矩阵方程、作为向量方程、作为线性方程组。
解的存在性
由上述关于矩阵方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b的定义可知:方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b有解当且仅当 b \boldsymbol b b是 A A A的各列的线性组合。
例:
设 A = [ 1 3 4 − 4 2 − 6 − 3 − 2 − 7 ] A = \begin{bmatrix}1 & 3 & 4 \\ -4 & 2 & -6 \\ -3 & -2 & -7\end{bmatrix} A=⎣⎡1−4−332−24−6−7⎦⎤, b = [ b 1 b 2 b 3 ] \boldsymbol b = \begin{bmatrix}b_1 \\ b_2 \\ b_3\end{bmatrix} b=⎣⎡b1b2b3⎦⎤,方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b是否对一切可能的 b 1 b_1 b1, b 2 b_2 b2, b 3 b_3 b3有解?
解:
把上述 A x = b A\boldsymbol x = \boldsymbol b Ax=b进行行化简可得:
[ 1 3 4 b 1 10 14 10 b 2 + 4 b 1 0 0 0 b 3 + 3 b 1 − 1 2 ( b 1 + 4 b 1 ) ] \begin{bmatrix}1 & 3 & 4 &b_1 \\ 10 & 14 & 10 & b_2 + 4b_1 \\ 0 & 0 & 0 & b_3 + 3b_1-\frac{1}{2}(b_1 + 4b_1)\end{bmatrix} ⎣⎡110031404100b1b2+4b1b3+3b1−21(b1+4b1)⎦⎤
明显的,要使得上述方程相容, b \boldsymbol b b必须满足:
b 1 − 1 2 b 2 + b 3 = 0 b_1-\frac{1}{2}b_2+b_3 = 0 b1−21b2+b3=0
这是 R 3 \mathbb R^3 R3中一个通过原点的平面,这个平面就是 A A A的3列的所有线性组合的集合。
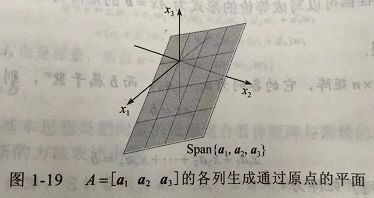
注意,该例中的方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b并非对所有的 b \boldsymbol b b都相容,这是因为 A A A的阶梯形含有零行。假如 A A A在所有三行都有主元,我们就不必注意增广列的计算,因为这时增广矩阵的阶梯形不可能产生形如 [ 0 0 0 1 ] [0 \quad 0 \quad 0 \quad 1] [0001]的行(对应下列的定理条目d)。
由此引出下面的定理:
定理:
设 A A A是 m × n m \times n m×n矩阵,则下列命题是逻辑上等价的。也就是说,对某个 A A A,它们都成立或者都不成立:
a. 对 R m \mathbb R^m Rm中每个 b \boldsymbol b b,方程 A x = b A\boldsymbol x = \boldsymbol b Ax=b有解。
b. R m \mathbb R^m Rm中的每个 b \boldsymbol b b都是 A A A的列的一个线性组合。
c. A A A的各列生成 R m \mathbb R^m Rm。
d. A A A在每一行都有一个主元位置。
注意,所谓的 A A A的各列生成 R m \mathbb R^m Rm,意思是 R m \mathbb R^m Rm中的每个向量 b \boldsymbol b b都是 A A A的线性组合,即 S p a n { v 1 , ⋯ , v p } = R m Span\{\boldsymbol v_1, \cdots, \boldsymbol v_p \} = \mathbb R^m Span{v1,⋯,vp}=Rm
A x A\boldsymbol x Ax的计算
可以从 A x A\boldsymbol x Ax的定义去计算 A x A\boldsymbol x Ax,也就是用 x \boldsymbol x x的各个元素分别去乘 A A A的各列,并进行累加。也可以通过证明得到如下快捷方式(证明略去):
若乘积 A x A\boldsymbol x Ax有定义,则 A x A\boldsymbol x Ax中的第 i i i个元素是 A A A的第 i i i行元素与 x \boldsymbol x x的相应元素乘积之和。
举例:
[ 1 0 0 0 1 0 0 0 1 ] [ r s t ] = [ 1 r 0 s 0 t 0 r 1 s 0 t 0 r 0 s 1 t ] = [ r s t ] \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}r \\ s \\ t\end{bmatrix} = \begin{bmatrix}1r & 0s & 0t \\ 0r & 1s & 0t \\ 0r & 0s & 1t\end{bmatrix} = \begin{bmatrix}r \\ s \\ t\end{bmatrix} ⎣⎡100010001⎦⎤⎣⎡rst⎦⎤=⎣⎡1r0r0r0s1s0s0t0t1t⎦⎤=⎣⎡rst⎦⎤
这个例子中矩阵的主对角线上元素为1,其他位置上元素为0,这个矩阵称为单位矩阵,记为 I I I,对 R n \mathbb R^n Rn中的任意 x \boldsymbol x x,有 I n x = x I_n \boldsymbol x = \boldsymbol x Inx=x。
矩阵-向量积 A x A\boldsymbol x Ax的性质
定理:
若 A A A是 m × n m \times n m×n矩阵, u \boldsymbol u u和 v \boldsymbol v v是 R n \mathbb R^n Rn中的向量, c c c是标量,则:
a. A ( u + v ) = A u + A v A(\boldsymbol u + \boldsymbol v) = A\boldsymbol u + A\boldsymbol v A(u+v)=Au+Av
b. A ( c u ) = c ( A u ) A(c\boldsymbol u) = c(A\boldsymbol u) A(cu)=c(Au)
根据矩阵和向量乘积的定义,简单以 R 3 \mathbb R^3 R3为例计算如下:
A ( u + v ) = [ a 1 a 2 a 3 ] [ u 1 + v 1 u 2 + v 2 u 3 + v 3 ] = ( u 1 + v 1 ) a 1 + ( u 2 + v 2 ) a 2 + ( u 3 + v 3 ) a 3 = ( u 1 a 1 + u 2 a 2 + u 3 a 3 ) + ( v 1 a 1 + v 2 a 2 + v 3 a 3 ) = A u + A v \begin{aligned}A(\boldsymbol u + \boldsymbol v) &= \begin{bmatrix}\boldsymbol a_1 & \boldsymbol a_2 & \boldsymbol a_3 \end{bmatrix} \begin{bmatrix}u_1 + v_1 \\ u_2 +v_2 \\u_3 + v_3\end{bmatrix}\\ &=(u_1 + v_1)\boldsymbol a_1 + (u_2 + v_2)\boldsymbol a_2 + (u_3 + v_3)\boldsymbol a_3\\ &=(u_1 \boldsymbol a1 + u_2 \boldsymbol a_2 + u_3 \boldsymbol a_3) + (v_1 \boldsymbol a_1 + v_2 \boldsymbol a_2 + v_3 \boldsymbol a_3) \\ &=A\boldsymbol u + A\boldsymbol v \end{aligned} A(u+v)=[a1a2a3]⎣⎡u1+v1u2+v2u3+v3⎦⎤=(u1+v1)a1+(u2+v2)a2+(u3+v3)a3=(u1a1+u2a2+u3a3)+(v1a1+v2a2+v3a3)=Au+Av
A ( c u ) = c ( A u ) A(c\boldsymbol u) = c(A\boldsymbol u) A(cu)=c(Au)也可以通过同样的方法得以证明。