【2016浙江省赛:区间取模】E : Modulo Query | ZOJ - 3940
2016浙江省赛:E 题 Modulo Query
【难度】
4.5 / 10 4.5/10 4.5/10
据说是卡银题?感觉有点难
【题意】
F ( i , X ) = { X m o d A 1 i = 1 F ( i − 1 , X ) m o d A i 2 ≤ i ≤ N F(i,X)= \begin{cases} X\mod A_1\quad i=1\\ F(i-1,X)\mod A_i \quad 2\le i\le N \end{cases} F(i,X)={XmodA1i=1F(i−1,X)modAi2≤i≤N
其中, A A A是一个长度为 N N N的整数数组,
X X X是不大于 M M M的非负整数。
现在给你了 N , A , M , Q N,A,M,Q N,A,M,Q
共 Q Q Q组询问,每组给你一个 Y Y Y
让你求出有多少个不同的 X X X满足 F ( N , X ) = Y \color{cyan}F(N,X)=Y F(N,X)=Y
对于第 i i i 个询问,若方案数为 Z i Z_i Zi
则答案累加上 i × Z i i\times Z_i i×Zi
最后输出最终的累加答案取模 1 0 9 + 7 10^9+7 109+7即可。
【数据范围】
2 ≤ N ≤ 1 0 5 2\le N\le 10^5 2≤N≤105
0 ≤ M ≤ 1 0 9 0\le M\le 10^9 0≤M≤109
1 ≤ A i ≤ 1 0 9 1\le A_i\le 10^9 1≤Ai≤109
1 ≤ Q ≤ 1 0 5 1\le Q\le 10^5 1≤Q≤105
0 ≤ Y i ≤ 1 0 9 0\le Y_i\le 10^9 0≤Yi≤109
Time limit:2000 ms
Memory limit:65536 kB
【输入样例】
T T T样例组数
N M N\ M N M
A 1 ⋯ A n A_1\cdots A_n A1⋯An
Q Q Q
Y 1 Y_1 Y1
⋮ \vdots ⋮
Y Q Y_Q YQ
1
3 5
3 2 4
5
0
1
2
3
4
【输出样例】
8
【解释】
每次查询的方案数分别为: 4 , 2 , 0 , 0 , 0 4,2,0,0,0 4,2,0,0,0
【思路】
【首先考虑下暴力做法】
化简那个奇怪的递归式子,无非就是让你求:
F ( N , X ) = X m o d A 1 m o d A 2 ⋯ m o d A n = Y F(N,X)=X\bmod A_1\bmod A_2\cdots \bmod A_n =Y F(N,X)=XmodA1modA2⋯modAn=Y
若我们暴力枚举 X X X,每次都计算出该式子的 Y Y Y,对于每个查询 Q Q Q都这么做的话:
时间复杂度为: O ( N × M × Q ) = 1 0 18 O(N\times M\times Q)=10^{18} O(N×M×Q)=1018
若我们计算完一次之后使用 u n o r d e r e d _ m a p unordered\_map unordered_map 记录每个数的答案的话:
时间复杂度为: O ( N × M ) = 1 0 14 O(N\times M)=10^{14} O(N×M)=1014
易 得 , 我 们 不 能 单 纯 让 X 暴 力 枚 举 [ 0 , M ] , 应 该 一 段 一 段 区 间 考 虑 \color{red}易得,我们不能单纯让X暴力枚举[0,M],应该一段一段区间考虑 易得,我们不能单纯让X暴力枚举[0,M],应该一段一段区间考虑
【从区间考虑】
(一)考虑下面一个例子:
X属于 [ 0 , 10 ] [0,10] [0,10], A 1 = 3 A_1=3 A1=3
我们简单枚举可得
| Y Y Y 查询数字 | Z Z Z相应答案 | X X X取值 |
|---|---|---|
| 0 | 4 | 0,3,6,9 |
| 1 | 4 | 1,4,7,10 |
| 2 | 3 | 2,5,8 |
| 3 | 0 | 无 |
首先对于取模运算,易得:取模后一定比取模数要小。
Y ≥ min i { A i } 时 , Z = 0 (1) \color{red}Y\ge\underset{i}{\min}\{A_i\}时,Z=0\tag{1} Y≥imin{Ai}时,Z=0(1)
然后我们分析一下每个 Y Y Y 对应的 Z Z Z 的规律。画一下图即可得知:
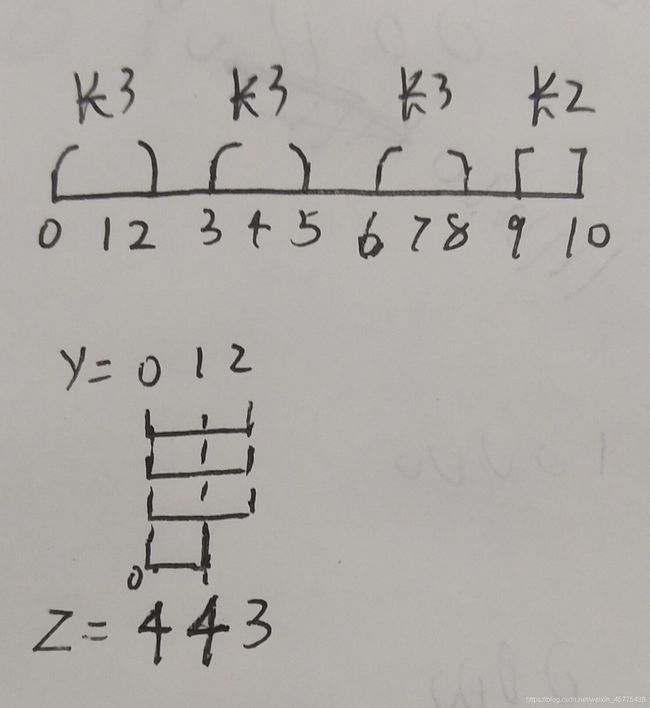
我们把区间 [ 0 , 10 ] [0,10] [0,10] 挖成三个 [ 0 , 2 ] [0,2] [0,2]的区间和一个 [ 0 , 1 ] [0,1] [0,1]的区间。
最后计算某个 Y Y Y 的时候,我们只要计算有多少个区间是包含这个Y即可。
(二)处理区间
但是有小伙伴说:你这区间怎么快速分割呀?一遍一遍for分割时间复杂度肯定超!
我们这就等价优化一下。
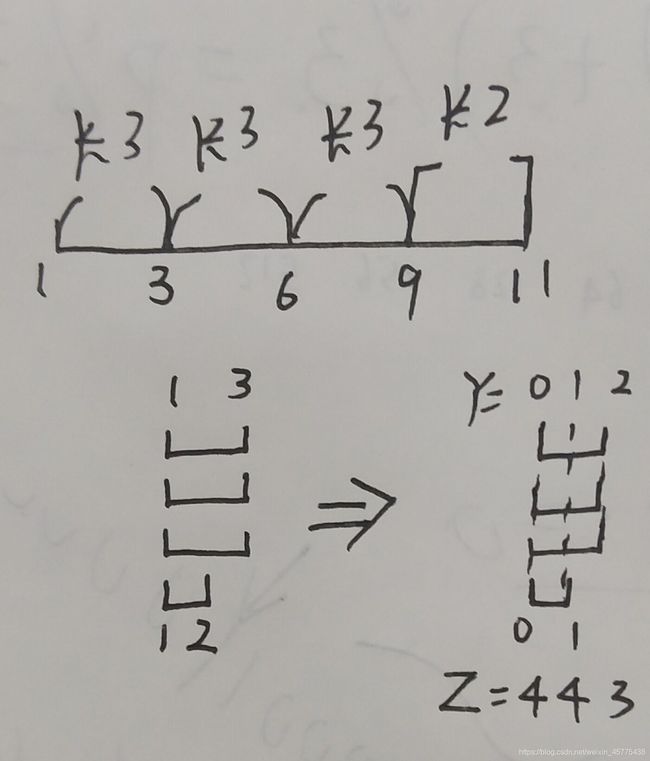
操作方法:
我 们 把 区 间 [ 0 , M ] 转 化 为 [ 1 , M + 1 ] 这 样 , 我 们 直 接 使 用 除 法 即 可 直 接 计 算 。 最 后 计 算 Y 的 时 候 , 每 个 区 间 长 度 再 转 化 成 从 0 开 始 的 区 间 即 可 。 \color{cyan}我们把区间[0,M]转化为[1,M+1]\\ \color{gray}这样,我们直接使用\pmb{除法}即可直接计算。\\ 最后计算Y的时候,每个区间长度再转化成从0开始的区间即可。 我们把区间[0,M]转化为[1,M+1]这样,我们直接使用除法除法除法即可直接计算。最后计算Y的时候,每个区间长度再转化成从0开始的区间即可。
上图的例子:M=10时,区间转化为 [ 1 , 11 ] [1,11] [1,11]
遇到 A 1 = 3 A_1=3 A1=3,该区间出现的小区间的段数为 ⌊ 11 / 3 ⌋ = 3 \lfloor11/3\rfloor=3 ⌊11/3⌋=3
那么剩余的一个小区间的长度为 11 m o d 3 = 2 11\bmod3=2 11mod3=2
更正式的语言描述:
若 你 现 在 有 一 个 区 间 [ 1 , P ] , 该 区 间 长 为 P 出 现 的 次 数 为 t i m 现 在 有 一 个 取 模 数 A i , A i < P , 那 么 该 模 数 会 把 区 间 进 行 取 模 分 割 多 出 来 的 小 区 间 [ 1 , A i ] 增 加 了 ⌊ P / A i ⌋ × t i m 个 若 A i ∤ P , 则 多 出 来 一 个 额 外 的 小 区 间 [ 1 , P m o d A i ] 增 加 了 t i m 个 (2) 若你现在有一个区间[1,P],该区间长为\color{green}P\color{w}出现的次数为\color{green}tim\color{w}\\ 现在有一个取模数A_i,A_i
由公式(1),若某个 A i A_i Ai 比你所拥有的区间长度还要大,那么就不必继续的区间分割了
可以使用 优 先 队 列 \color{red}优先队列 优先队列完成吗?显然 不 行 \color{red}不行 不行。
若我们多出来的区间 [ 1 , A i ] [1,A_i] [1,Ai]或者 [ 1 , P m o d A i ] [1,P\bmod A_i] [1,PmodAi] 是已有的,那么优先队列里的相同元素会越来越多。
这样,我们使用 M a p \color{red}Map Map 即可。它可以轻松记录某个区间出现的次数,可以随时 O ( log N ) O(\log N) O(logN)修改增删,并且有序,可以类似优先队列优先拿出区间较大的出来。
【小技巧:】
M a p Map Map 优先拿出的是第一个元素值较小的元素,若我们往里添加某个数的负数,则可以优先拿出原来元素值较大的元素。拿出来后再取反即可。
(三)处理询问
我们怎么知道某个数字在多少个之前处理的区间范围内的?
首先,我们按区间长度由小到大排列。然后记录前缀和即可。
a a [ i ] 表 示 区 间 长 度 第 i 小 的 区 间 的 长 度 p r e [ i ] 记 录 区 间 次 数 的 前 缀 和 , p r e [ i ] = ∑ i j = 1 a a [ j ] 的 t i m \color{green}aa[i]表示区间长度第i小的区间的长度\\ pre[i]记录区间次数的前缀和,pre[i]=\underset{j=1}{\overset{i}{\sum}}aa[j]的tim aa[i]表示区间长度第i小的区间的长度pre[i]记录区间次数的前缀和,pre[i]=j=1∑iaa[j]的tim
对于某个查询的 Y Y Y ,我们知道该数的出现次数为:
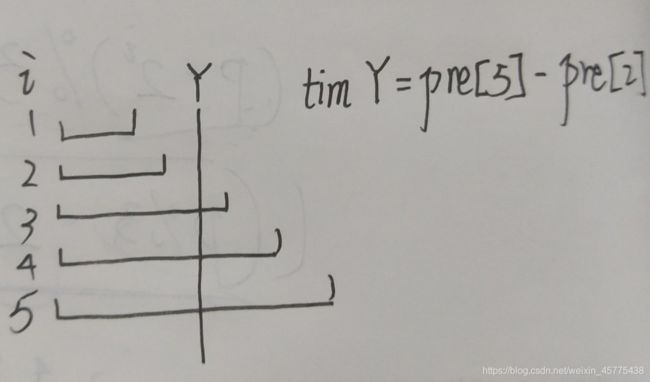
对 于 某 个 Y , 该 Z = p r e [ T o t ] − p r e [ L ] 其 中 T o t a l 为 最 大 的 i L = max i { i ∣ a a [ i ] < Y } (3) 对于某个Y,该\color{red}Z=pre[Tot]-pre[L]\color{w}\\ 其中\color{w}Total为最大的i\\ \color{red}L=\underset{i}{\max}\{i\big | aa[i]
注意式子(3),不能取等于号。
我们使用 l o w e r _ b o u n d \color{red}lower\_bound lower_bound 即可算出 L L L
【核心代码】
时间复杂度: O ( N log N + Q log N ) O(N\log N+Q\log N) O(NlogN+QlogN) 应该是很松的上界,紧上界可以看其他dl的证明
Time(ms):63 (不使用快读为278ms)
Mem(MB):1.1
/*
_ __ __ _ _
| | \ \ / / | | (_)
| |__ _ _ \ V /__ _ _ __ | | ___ _
| '_ \| | | | \ // _` | '_ \| | / _ \ |
| |_) | |_| | | | (_| | | | | |___| __/ |
|_.__/ \__, | \_/\__,_|_| |_\_____/\___|_|
__/ |
|___/
*/
const int MAX = 1e5+50;
map<ll,ll>M;
ll aa[MAX];
ll pre[10*MAX];
int main()
{
int T;
T = read();
while(T--){
M.clear();
int n;
ll m;
n = read();
m = read_ll();
ll bef = m + 1LL; /// 原区间长转化为[1,M+1]
M[-bef] = 1LL; /// 添加负数即可以每次取出最长的区间
for(int i=1;i<=n;++i){
ll now = read_ll();
if(now >= bef)continue; /// 公式(1)
bef = now;
for(map<ll, ll>::iterator it = M.begin(); it != M.end();){
ll chang = -it->first;
ll tim = it->second;
if(chang <= now)break; /// 公式(1)
ll more = chang / now;
ll another = chang % now;
map<ll, ll>::iterator itr = it;
it++;
M.erase(itr); /// erase it
M[-now] += tim * more; /// 公式(2)
if(another!=0)M[-another] += tim; /// 公式(2)
}
}
int cnt = 0;
aa[0] = 0LL;
for(map<ll, ll>::reverse_iterator rit = M.rbegin(); rit != M.rend();rit++){
ll chang = -rit->first - 1; /// 倒序遍历即从小到大排序
ll tim = rit->second;
aa[++cnt] = chang;
pre[cnt] = pre[cnt-1] + tim; /// 前缀和记录
}
ll Q;Q = read_ll();
ll Z = 0LL;
for(ll i = 1;i <= Q; ++i){
ll y;
ll ans = 0LL;
y = read_ll();
if(y >= bef)continue; /// 公式(1)
ll di = lower_bound(aa,aa+cnt+1,y) - aa;
if(di && aa[di] >= y)di--;
Z = Z + i * (pre[cnt] - pre[di]) % MOD; /// 公式(3),乘上i是题目要求
Z %= MOD;
}
printf("%lld\n",Z);
}
return 0;
}