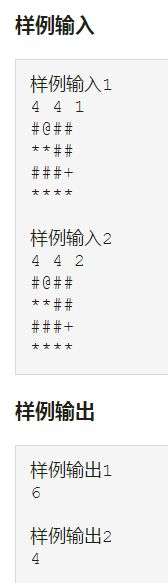
【典型带状态的dfs搜索+多重剪枝】鸣人和佐助

因为题目是OpenJudge的，似乎需要额外的code才能进去就不放链接了;(

题目

佐助被大蛇丸诱骗走了，鸣人在多少时间内能追上他呢？
已知一张地图（以二维矩阵的形式表示）以及佐助和鸣人的位置。
地图上的每个位置都可以走到，只不过有些位置上有大蛇丸的手下，需要先打败大蛇丸的手下才能到这些位置。鸣人有一定数量的查克拉，每一个单位的查克拉可以打败一个大蛇丸的手下。
假设鸣人可以往上下左右四个方向移动，每移动一个距离需要花费1个单位时间，打败大蛇丸的手下不需要时间。如果鸣人查克拉消耗完了，则只可以走到没有大蛇丸手下的位置，不可以再移动到有大蛇丸手下的位置。佐助在此期间不移动，大蛇丸的手下也不移动。请问，鸣人要追上佐助最少需要花费多少时间？
输入
输入的第一行包含三个整数：M，N，T。代表M行N列的地图和鸣人初始的查克拉数量T。0 < M,N < 200，0 ≤ T < 10
后面是M行N列的地图，其中@代表鸣人，+代表佐助。*代表通路，#代表大蛇丸的手下。 输出
输出
包含一个整数R，代表鸣人追上佐助最少需要花费的时间。如果鸣人无法追上佐助，则输出-1。
时间限制1000ms

思路

啊手痒想写bfs，但是这题dfs可以过而且代码量会少一些！
我们首先写一个正常的dfs，看看效果！

（一）本体代码

因为从起点到终点有多条路径，我们选择把能走的路径都走一遍，然后比较哪次更短一些。

多条路径的方向用两个方向函数可以减少许多代码量。

注意有查克拉的限制，查克拉<0则无法走了。

#include 
#define show(x) std::cerr << #x << "=" << x << std::endl
#define IOS ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
using namespace std;
/**
    freopen("input.in", "r", stdin);
    freopen("output.out", "w", stdout);
*/
typedef long long ll;
const int MAX=220;
const int INF=1e9;
const double EPS = 0.00001;
const ll MOD=1e9+7;
int m,n,t;
int ans;
int sx,sy,ex,ey;
char M[MAX][MAX];
bool vis[MAX][MAX];
int dix[] = {0,0,-1,1};
int diy[] = {-1,1,0,0};
void dfs(int x,int y,int d,int k){///走到(x,y)花了d步，还有k查克拉
    if(k<0)return;
    for(int i=0;i<4;++i){
        int tx=x+dix[i];
        int ty=y+diy[i];
        if(x<1 || y<1 || x>m || y>n || vis[tx][ty])continue;///判断越界与重复
        vis[tx][ty]=1;///bfs的vis操作
        if(M[tx][ty]=='*')dfs(tx,ty,d+1,k);
        else if(M[tx][ty]=='#')dfs(tx,ty,d+1,k-1);
        else if(M[tx][ty]=='+')ans=min(ans,d+1);
        vis[tx][ty]=0;///bfs的vis恢复（回溯）操作
    }
}
int main()
{
    ///IOS;
    cin >> m >> n >> t;
    for(int i=1;i<=m;++i){
        for(int j=1;j<=n;++j){
            cin >> M[i][j];
            if(M[i][j]=='@'){
                sx=i;
                sy=j;
            }
            if(M[i][j]=='+'){
                ex=i;
                ey=j;
            }
        }
    }
    ans = INF;
    vis[sx][sy]=1;
    dfs(sx,sy,0,t);
    cout << ans;
    return 0;
}

看一下结果：

看来需要剪枝呀！那就剪起来！

（二）距离剪枝1

如果现在坐标是(tx,ty)，终点坐标是(ex,ey)，那么我至少还需要走的距离
p=abs(x-ex)+abs(y-ey) ，也叫曼哈顿距离。
如果我现在走到(tx,ty)已经走了d步，之前走到终点的最短可行距离是ans

如果p+d>=ans ，那就不需要再进行搜索了，直接回溯即可

开心提交，一看结果：

我再想办法！

（三）距离剪枝2

我们假设走到(x,y)的一个解为距离d_x,y ,查克拉剩余 C_x,y
（1）如果我们另一种方法也走到了这个点，并且现在的距离比d_x,y大，现在的查克拉比 C_x,y少，那么这个点有点菜，我们可以回溯掉。
（2）如果我们另一种方法也走到了这个点，并且现在的距离比d_x,y小，现在的查克拉比 C_x,y多，那么这个点很爽啊，我们更新掉原来的距离d_x,y ,查克拉剩余 C_x,y

代码更新一下！

	if(d<=dis[x][y] && k>=cha[x][y]){
        dis[x][y]=d;
        cha[x][y]=k;
    }else if(d>=dis[x][y] && k<=cha[x][y]){
        return ;
    }

欢天喜地提交，然后结果：

？我就一个表情在这里。看来还需要更妙的方法。

（四）终极剪枝

就像dp一样，我们存储每个点的状态

一个点的状态有：横坐标x ，纵坐标y ，已走距离d ， 剩余查克拉k

我们最终是需要求距离的最小值的，那么我们设置一个类似于dp数组的高维数组来记录每次的状态：

int dis[x][y][k]; 表示走到(x,y)且剩余查克拉为k的最小已走距离。

我们每次只需判断这个距离，如果比它小，更新；如果比它大，回溯。

完整代码搞起！

#include 
#define show(x) std::cerr << #x << "=" << x << std::endl
#define IOS ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
using namespace std;
/**
    freopen("input.in", "r", stdin);
    freopen("output.out", "w", stdout);
*/
typedef long long ll;
const int MAX=220;
const int INF=1e9;
const double EPS = 0.00001;
const ll MOD=1e9+7;
int m,n,t;
int ans;
int sx,sy,ex,ey;
char M[MAX][MAX];
bool vis[MAX][MAX];
int dis[MAX][MAX][15];
int dix[] = {0,0,-1,1};
int diy[] = {-1,1,0,0};
void dfs(int x,int y,int d,int k){
    if(k<0)return;
    if(d<dis[x][y][k]){			///这里究极剪枝！
        dis[x][y][k]=d;
    }else return;
    for(int i=0;i<4;++i){
        int tx=x+dix[i];
        int ty=y+diy[i];
        if(x<1 || y<1 || x>m || y>n || vis[tx][ty])continue;
        if(abs(x-ex)+abs(y-ey)+d>=ans)continue;
        vis[tx][ty]=1;
        if(M[tx][ty]=='*')dfs(tx,ty,d+1,k);
        else if(M[tx][ty]=='#')dfs(tx,ty,d+1,k-1);
        else if(M[tx][ty]=='+')ans=min(ans,d+1);
        vis[tx][ty]=0;
    }
}
int main()
{
    ///IOS;
    cin >> m >> n >> t;
    for(int i=1;i<=m;++i){
        for(int j=1;j<=n;++j){
            cin >> M[i][j];
            if(M[i][j]=='@'){
                sx=i;
                sy=j;
            }
            if(M[i][j]=='+'){
                ex=i;
                ey=j;
            }
            for(int k=0;k<10;++k)dis[i][j][k]=INF;
        }
    }
    /**for(int i=1;i<=m;++i){
        for(int j=1;j<=n;++j)
            cout << M[i][j];
        cout << endl;
    }*/
    ans = INF;
    vis[sx][sy]=1;
    dfs(sx,sy,0,t);
    if(ans==INF)cout << -1;
    else cout << ans;
    return 0;
}

最后欢天喜地AC成功！

呃呃，找错图片了，是这个！

快乐剪枝之旅