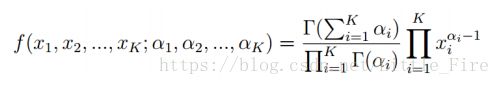LDA（Dirichlet Distribution）主题模型基本知识与理解（一）

 最近在研究无监督模型与降维技术，说起无监督模型，我们首先想到的是聚类技术（Clustering），而在实际生产中，很多方法可以被用来做降维（正则化Lasso/Ridge回归、PCA主成分分析、小波分析、线性判别法、拉普拉斯特征映射等），其中基于主成分分析（PCA）的Topic Model技术包含了pLSA、LDA、SVD分解等。+

本文为大家科普一下，作为一名机器学习相关工作者，本人对LDA的基本理解。LDA的学习和研究真的是一个让人头大的事情，我这里也是参考了一些资料之后，做的一点总结。本文是第一部分，后面还会有第二部分的撰写，各位大牛，如果觉得总结的还不错，麻烦留个言、点个赞，多谢各位打赏

（一）LDA简单描述

以下是LDA在百科中的解释：

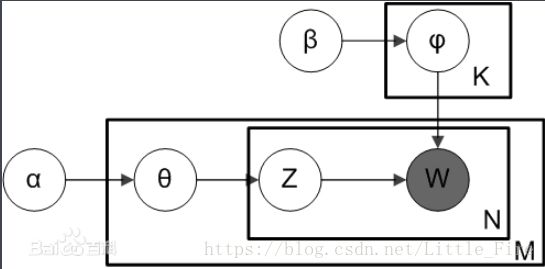
LDA于2003年由 David Blei, Andrew Ng和 Michael I. Jordan提出，因为模型的简单和有效，掀起了主题模型研究的波浪。LDA（Latent Dirichlet Allocation）是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，模型中包含词语（W）、主题（Z）和文档（theta）三层结构。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。

从公式角度分析，Dirichlet分布是一个多变量生成式的beta分布，如下所示：

对于Dirichlet Distribution的实现与理解：

首先给定一个概率分布，可能是低维或高维空间的概率分布（例如正态分布X~N(mu, sigma)），在样本空间上根据正态分布进行采样，采样到一个数据（低维空间上采样到一个点，高维空间上采样到一个向量），由于Dirichlet Distribution进行的是高维空间的采样，故得到向量x。

根据狄利克雷分布的性质，采样得到的x向量各维度的值加和为1，即，例如三维向量x=（0.3,0.5,0.2），即每个维度值x1=0.3、x2=0.5、x3=0.2可作为其他变量的概率密度。

因此，Dirichlet Distribution被称为采样的分布，或者称为分布的分布。

（二）Dirichlet分布及其性质

接下来我们来研究一下alpha取值，对于Dirichlet Distribution的影响程度，如下所示：

如果α1=α2=α3=1（图a所示），采样平面均匀，在这个三角面中所有点被采样的概率相同；

如果α1=α2=α3=k（k！=1），此时采样空间对称，但不均匀，当k>1时（如图b），中间区域样本被采样的概率更高，边缘区域被采样概率低；当k<1时（图e），采样情况刚好相反。

如果α1、α2、α3不全相等，则采样区域趋近于数值较大α的那个维度。

这样，我们讲到的Dirichlet Distribution就可以作为其他变量的分布。

接下来，为大家描述一个掷硬币的场景，我们观测到的掷硬币状态包括1（正面）和0（反面），用x表示观测硬币的状态，假设观测到的硬币状态又一个隐变量z控制，z表示投掷A硬币的状态，若z=1表示投掷B硬币，z=0投掷C硬币，而我们观测的硬币序列是由B硬币和C硬币的正反面共同生成的。且A硬币的投掷分布由π决定，即A~π，同理有B~p，C~q

于是观测值x由隐含变量z控制，z又由π控制，此时，生成的状态转换图如下，其中xi、zi表示第i个时刻观测值与隐含值

当待解决问题是投掷硬币时z存在两个状态值（A硬币投掷的正面或反面），z=0或z=1，就存在π和1-π两个值决定。若问题是投色子问题，z=1、2、3、4、5、6，对应的“π”就有6个值π1、π2、π3、π4、π5和π6，且满足：，代表了隐变量初始时候的概率分布。

此时，我们假设π是我们每次采样的部分（π在这里是个parameter，给定了π就会决定z的取值，因为z的采样由其概率分布π决定）。此时将π当成一个随机变量variable，可以向上走一层，即假定π也是随机采样得到的，而π的随机采样又由α决定，即原状态转换图变成了如下形式：

 

此时，π是由α控制的随机变量，满足由α决定的Dirichlet分布π~dir(α)，这个分布有多少维就由π的取值决定。如果是掷硬币问题，π的取值0、1，dir(α)分布就可以决定π的分布是（0.3，0.7），（0.4，0.6）等；如果是掷骰子，那么π的取值1~6，dir(α)分布就可以决定π的分布也是6维的。

这样一来，π~dir(α)，z~p(π)，x~p(z)，即π由以α为参数的Dirichlet采样生成，z由关于π的采样生成，而观测值x则由z的采样生成。

我们知道，LDA的定义和主要应用并非掷硬币和掷骰子，而是NLP。掷硬币和掷骰子这两种应用都是用EM算法和HMM可以很好解决，在第二部分，我们会讲解LDA在NLP方面的应用。