leetcode(5) 最长回文字串

       最长回文子串问题的描述很简单，给定一个字符串 s，找到 s 中最长的回文子串。例如我们的字符串是 babd，那么最长的回文子串就是 bab，也就是正反两个方向都是一致的。

       我写的算法是中点拓展法。长度为 n 的字符串我们可以看成 2*n - 1  个点，即字符本身和字符中间的位置都是我们拓展的点。显然这种算法的复杂度是 O(n^2)，还是属于该复杂度中计算量较大的。因为凭空添加了一些节点来计算，所以比较麻烦。具体代码如下，已经是经过我的一部分精简，删除了一些不必要的语句和过程变量，在没有修改之前只是击败了 10%，修改之后击败了 66%。

        其中一个容易忽略的点就是，例如 babd 这个字符串，我们以 a 作为中点来拓展。那么左边有一个位置可以延伸，右边有两个位置可以延伸，一和二取小的那个，也就是我们代码中的 for j in range(min(p, l - 1- p)) 和 for j in range(min(p, l - p))。有了这个边界的限制就不会出现 index out of range 的错误。

class Solution:
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) <= 1:
            return s
        else:
            max_string = s[0]
            l = len(s)
            for i in range(2*l - 1):
                if i%2 == 0:
                    p = int(i/2)
                    for j in range(min(p, l - 1 - p)):
                        if s[p - 1 - j] == s[p + 1 + j]:
                            continue
                        else:
                            if 2*j + 1 > len(max_string):
                                max_string = s[p - j:p + 1 + j]
                            break
                    else:
                        j = min(p, l - 1 - p)
                        max_string = s[p - j:p + 1 + j] if 2*j + 1 > len(max_string) else max_string
                elif i%2 != 0:
                    p = int((i+1)/2)
                    for j in range(min(p, l - p)):
                        if s[p - 1 - j] == s[p + j]:
                            continue
                        else:
                            if 2*j > len(max_string):
                                max_string = s[p - j:p + j]
                            break
                    else:
                        max_string = s[p - (j + 1): p + j + 1] if 2*(j + 1) > len(max_string) else max_string
            return max_string
                

          但是仍觉得很繁琐，于是看了几个前面靠前的算法，学习一下别人的思路。代码如下，看的时候完全无法理解其中的逻辑，所以我用 visio 做了一张示意图来理解。

class Solution:
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        n = len(s)
        if n < 2 or s == s[::-1]:
            return s
        max_len = 1
        start = 0
        for i in range(1,n):
            even = s[i-max_len:i+1]
            odd = s[i-max_len-1:i+1]
            if i-max_len-1>=0 and odd == odd[::-1]:
                start = i-max_len-1
                max_len += 2
                continue
            if i-max_len>=0 and even == even[::-1]:
                start = i-max_len
                max_len += 1
        return s[start:start+max_len]

         自己捋了一遍之后明白了，它本质上也是一种历遍的思维，只不过相比我们规定以某个位置作为中点来拓展的方法，他巧妙地以某个位置作为考察字串的右端点。例如，首先我们判断以第二个元素结尾的子串，包括奇数和偶数(实际上只有偶数，奇数必须不小于3所以没意义)，判断之后发现都不是回文，所以目前最长的长度仍然是 1；然后考察以第三个元素结尾的子串，有一个奇数长度和一个偶数长度，经判断奇数长度 DCD 是回文，而偶数长度的  CD 不是，于此我们更新参数 start  = 0 和 max_len = 3 来描述我们当前所找到的最长回文子串。以此类推，每往后延长一个单位，即 i 增加 1，我们会考虑两个子串，一个长度为 max_len + 1 另一个为 max_len + 2，如果其中有一个是回文串我们就可以更新我们的最长回文子串。

        有的人可能会怀疑这样子会不会漏过一些隐藏的，例如我们目前匹配了很长一串了，其中找到一个长度为 2 的最长，然后每次只考虑 长度为 3 和 4，会不会漏过一些长度大于 4 的回文串？答案是否定的，用 DDCACDB 来举个例子，一开始很显然就是 DD，而 "DCACD" 这个串的右端点是 "D" 在第 6 个位置，那么当我们的历遍进行到第 5 个位置 "C" 的时候就已经发现了这个"DCACD" 中的 "CAC" 长度大于 "DD" 了。也就是说，max_len 的变化总是以 1 或者 2 作为 interval 的。所以以上的算法是没问题的。

        这个别人的优质算法，启发了我，如果想要获得快捷简便的算法，就要设法运用每一次的计算结果，尽量避免重复无意义的计算。虽然这样子不一定可以达到在时间复杂度上的最优，但是在处理很多规模没有非常庞大的问题时，往往可以得到用时较短的解答。

       官方给出的推荐答案中，有一个时间复杂度为 O(n) 的 Manacher Algorithm，很多资料都称之为马拉车算法。它的核心思想也是与我自己写的算法相似的中点拓展法中的一致，但是它采取了一些技巧和中间变量来使得，我们每一步计算中的结果都不会浪费，也不必要进行重复的计算。我看了一些关于 Manacher 算法的文章，一开始真的一头雾水，慢慢地才得以理解，实际上不是很复杂，接下来借助图片来讲解何为 Manacher 算法。

Manacher Algorithm

       回顾中点拓展的算法，我们把长度为 n 的字符串延伸出 2*n - 1 个节点，那是因为我们要考虑回文串可能有奇数和偶数两种情况。为了避免在区分这两种情形时的麻烦，Manacher 算法第一步是在每个字符串左右填充上一个符号，当然，这个符号不能已经存在于字符串中，否则就混乱了。填充之后，无论原本是奇数还是偶数的回文串都变成了奇数长度。

ACDAD         #A#C#D#A#D#         len("#D#A#D#")=7

ECDDCA         #E#C#D#D#C#A#         len("#C#D#D#C#")=7

         那么假设，我们在新的字符串中找到了最长回文子串，要如何得到在原字符串中的最长回文子串呢？难道是把添加的符号去掉之后再看看对应的部分吗？显然这样子有点笨，我们可以看到例如在 #A#C#D#A#D# 的最长回文子串的半径是 4，中点是第二个 A。那么这个字串中，# 号的数量是比字符要多一个的，所以对应到原字符串的最长回文子串的长度是 3。严谨一些来建立数量关系，我们先定义一个数组来和新字符串对应，数组中的值是新字符串中对应位置的元素，以该元素为中点所能得到的最长回文子串的半径。举两个完整的例子如下，我们将这个数组命名为 Len。

# A # C # D # A # D #

1 2 1 2 1 2 1 4 1 2 1

# E # C # D # D # C # A #

1 2 1 2 1 2 5 2 1 2 1 2 1

       那么根据我们上面所说的，以第 i(i >= 0) 个元素为中点的最长回文串的半径为 Len(i)，假设对应的原字符串中的最长回文子串的长度为 x，有简单的数量关系

2 * Len(i) - 1 = 2 * x + 1

解得 x = Len(i) - 1。所以，我们最初的问题得以转化成，求 Len 数组中的最大值，将最大值减 1，就得到了原字符串中的最长回文子串的长度。

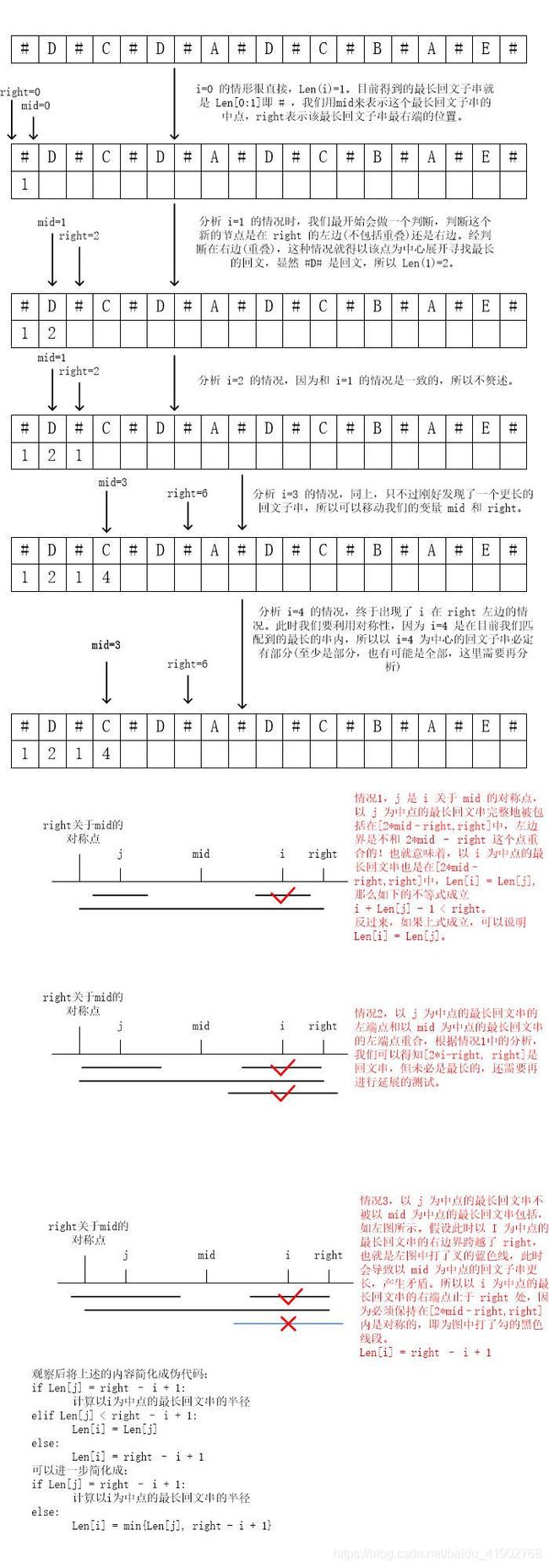
        在求 Len 的过程中，我们会关心并更新两个变量 mid 和 right。结合图片来理解这两个变量的含义以及作用，会比直接讲这两个变量的定义来得更容易理解。具体的推导过程如下。

         给出我写的代码，虽然最后计算的结果不如人意，甚至没有我第一个算法快。一方面是这个算法其中有比较多的判断分支，虽然复杂度不至于是 O(n^2)，但是步骤太多导致运算速度不快；另一方面要维护过程变量，也是需要空间。总的来说还是第二个要优秀。

class Solution:
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) <= 1:
            return s
        else:
            self.s = '#' + '#'.join(s) + '#'
            Len = [1]
            mid, right = 0,0
            for i in range(1, len(self.s)):
                if i < right:
                    j = 2*mid - i
                    if Len[j] == right - i + 1:
                        r = self.findradius(i)
                        Len.append(r)
                        if r >= right - mid + 1:
                            mid = i
                            right = mid + r - 1
                    else:
                        Len.append(min(Len[j], right - i + 1))
                else:
                    r = self.findradius(i)
                    Len.append(r)
                    if r >= right - mid + 1:
                        mid = i
                        right = mid + r - 1
            return s[int((right + 1)/2) - max(Len) + 1: int((right + 1)/2)]
                
    def findradius(self, i):
        j = 1
        while i - j >= 0 and i + j <= len(self.s) - 1:
            if self.s[i - j] == self.s[i + j]:
                j += 1
                continue
            else:
                return j
        return j