图论基础知识_图论基础
图论基础知识
In this article, we’ll touch upon the graph theory basics. Graph Theory is a branch of mathematics that aims at studying problems related to a structure called a Graph.
在本文中,我们将介绍图论的基础知识。 图论是数学的一个分支,旨在研究与称为图的结构有关的问题。
In this article, we will try to understand the basics of Graph Theory, and also touch upon a C programmer’s perspective for representing such problems.
在本文中,我们将尝试了解图论的基本知识,并涉及C程序员表示此类问题的观点。
什么是图? (What is a Graph?)
A Graph is a structure that consists of a set of nodes/vertices that map to a set of edges. How do they map together?
图是由映射到一组边的一组节点/顶点组成的结构。 他们如何一起绘制地图?
Well, the words themselves give you a hint. A node/vertex is a point on the graph, and edges join two vertices together, through a line segment. We represent an edge joining a pair of vertices by => edge = (u, v)
好吧,这些单词本身会给您一个提示。 节点/顶点是图形上的一个点,边通过线段将两个顶点连接在一起。 我们用=> edge =(u,v)表示连接一对顶点的边
The below figure represents a Graph having 3 vertices and 2 edges. We don’t need to connect all the vertices together in a graph.
下图表示具有3个顶点和2个边的Graph。 我们不需要将图中的所有顶点连接在一起。
Now that you know what a Graph is, let’s look at the types of Graphs.
现在您知道了什么是图,让我们看一下图的类型。
图的类型 (Types of Graphs)
The highest level of demarcation is based on the direction.
最高级别的划分基于方向。
That is, there are two types of graphs based on this category: Undirected and Directed.
也就是说,还有基于该分类两种类型的图表: 无向和定向 。
无向图 (Undirected Graph)
An undirected graph is a graph where every edge is represented as an unordered pair e = (1, 2). This means that the order doesn’t matter to us, since (1, 2) is the same as (2, 1).
无向图是其中每个边缘都表示为无序对 e =(1,2)的图 。 这意味着顺序对我们来说无关紧要,因为(1,2)与(2,1)相同 。
All graphs which do not have an arrow between vertices are called Undirected Graphs.
所有在顶点之间没有箭头的图称为无向图。
有向图 (Directed Graph)
A directed graph is a graph where every edge is directed (unidirectional). This means that the edges e1 = (1, 2) and e2 = (2, 1) are different.
有向图是每个边都指向(单向)的图。 这意味着边缘e1 =(1,2)和e2 =(2,1)不同。
They represent oppositely directed edges between 1 and 2.
它们代表介于1和2之间的相反方向的边缘 。
We represent any connection by an arrow mark to show the direction of the edge.
我们用箭头标记表示任何连接以显示边缘的方向。
These are the two major types of Graphs, which themselves have different divisions. We will continue to cover this topic as we go along in the future.
这是图的两种主要类型,它们本身具有不同的划分。 将来,我们将继续涵盖这个主题。
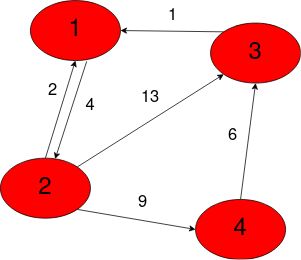
加权图 (Weighted Graphs)
There is one more type of graph, called a Weighted Graph, which we use in a lot of problems.
图还有另一种类型,称为加权图 ,我们在很多问题中都使用了它。
This is simply any directed/undirected graph with each edge having a weight/cost associated with it.
这仅仅是任何有向/无向图,每个边都有与之关联的权重/成本。
Now that we know the basics of graphs, let us look at the implementation of these graphs in C.
既然我们已经了解了图的基础知识,那么让我们看一下这些图在C中的实现。
图的实现 (Implementation of Graphs)
There are two ways of implementing a graph.
有两种实现图的方法。
- Adjacency Matrix 邻接矩阵
- Adjacency List 邻接表
使用邻接矩阵 (Using Adjacency Matrices)
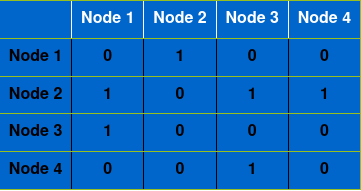
An Adjacency Matrix adj is a matrix where:
邻接矩阵 adj是一个矩阵,其中:
- adj[i][j] = 1 if (i, j) has an edge connecting them 如果(i,j)具有连接它们的边,则adj [i] [j] = 1
- adj[i][j] = 0 otherwise adj [i] [j] = 0否则
This has the advantage of an O(1) time complexity for searching and updating values, but has a space complexity of O(n^2).
这具有用于搜索和更新值的O(1)时间复杂度的优点,但具有O(n ^ 2)的空间复杂度。
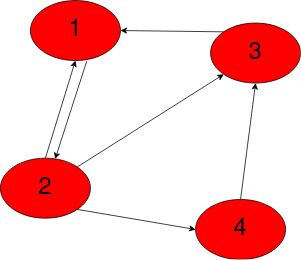
For the directed graph below, let’s figure out the adjacency matrix.
对于下面的有向图,让我们找出邻接矩阵。
We denote the matrix to have the element adj[i][j] = 1 only if there is a directed edge from i to j.
我们表示只有在从i到j的有向边的情况下 ,才使元素adj [i] [j] = 1的矩阵。
Constructing the matrix is very simple, so let’s quickly look at an example in C. Here, we implement the adjacency matrix as a 2D-array.
构造矩阵非常简单,因此让我们快速看一下C语言中的示例。在这里,我们将邻接矩阵实现为2D数组。
The implementation is as below. Code is self-explanatory for anyone familiar with C programming and pointers.
实现如下。 对于熟悉C编程和指针的任何人来说,代码都是不言自明的。
/**
Code for https://journaldev.com article
Purpose: Adjacency Matrix representation of a Graph
@author: Vijay Ramachandran
@date: 10-02-2020
*/
#include
#include
typedef struct Graph Graph;
struct Graph {
// Number of vertices
int v;
// Adjacency Matrix
int** adj;
};
int** init_adjacency_matrix(Graph g) {
// Initializes an adjacency matrix for the graph
if (g.adj)
return g.adj;
// Allocates memory for the matrix
// and sets every element to 0
int** matrix = (int**) calloc (g.v, sizeof(int*));
for (int i=0; i g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
exit(1);
}
g.adj[i-1][j-1] = 1;
}
void remove_edge(Graph g, int i, int j) {
// Sets the edge from i to j as zero
if (!g.adj) {
fprintf(stderr, "Adjacency Matrix not initialized!\n");
exit(1);
}
else if (i > g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
exit(1);
}
g.adj[i-1][j-1] = 0;
}
int check_if_exists(Graph g, int i, int j) {
// Checks if there is an edge from vertex i to j
if (!g.adj) {
fprintf(stderr, "Adjacency Matrix not initialized!\n");
exit(1);
}
else if (i > g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
return 0;
}
return g.adj[i-1][j-1];
}
int main() {
// Graph with 4 vertices
Graph g = {4, NULL};
printf("Created a Graph Structure with %d vertices\n", g.v);
g.adj = init_adjacency_matrix(g);
// Let's connect the 4 vertices using 6 edges
add_edge(g, 1, 2);
add_edge(g, 2, 1);
add_edge(g, 2, 3);
add_edge(g, 2, 4);
add_edge(g, 3, 1);
add_edge(g, 4, 3);
// Check if the edge is connected
printf("Is there an edge from 1 to 2?\n");
if (check_if_exists(g, 1, 2))
printf("Yes\n");
else
printf("No\n");
printf("Is there an edge from 4 to 3?\n");
if (check_if_exists(g, 4, 3))
printf("Yes\n");
else
printf("No\n");
printf("Is there an edge from 1 to 3?\n");
if (check_if_exists(g, 1, 3))
printf("Yes\n");
else
printf("No\n");
free_matrix(g);
return 0;
}
Output
输出量
Created a Graph Structure with 4 vertices
Initialized Adjacency Matrix!
Is there an edge from 1 to 2?
Yes
Is there an edge from 4 to 3?
Yes
Is there an edge from 1 to 3?
No
The problem is that we always need to use O(n^2) elements for storage, and hence, we often use adjacency lists to represent graphs.
问题在于,我们总是需要使用O(n ^ 2)个元素进行存储,因此,我们经常使用邻接表来表示图。
使用邻接表 (Using Adjacency Lists)
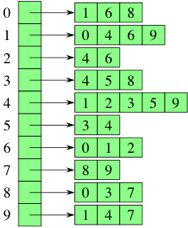
An Adjacency List is a list that can be used to represent connected vertices.
邻接列表是可用于表示连接的顶点的列表。
The idea is to store a linked list for vertex, that consists of all vertices which are directly connected to it.
这个想法是存储顶点的链表,该链表包括直接连接到它的所有顶点。
We can implement this using an array of linked lists.
我们可以使用一系列链接列表来实现。
A simple implementation in C is given below.
下面给出了一个使用C的简单实现。
/**
Code for https://journaldev.com article
Purpose: Adjacency List representation of a Graph
@author: Vijay Ramachandran
@date: 10-02-2020
*/
#include
#include
typedef struct Graph Graph;
typedef struct Node Node;
struct Node {
// To represent the linked list node.
// Contains the vertex index
int vertex;
// And a pointer to the next element in the linked list
Node* next;
};
struct Graph {
// Number of vertices
int v;
// Array of Adjacency Lists
Node** adj_lists;
};
Node** init_adjacency_lists(Graph g) {
// Initializes an adjacency matrix for the graph
if (g.adj_lists)
return g.adj_lists;
// Allocates memory for the lists
// There is a list for every vertex in the graph
// which means there are g.v adjacent lists
Node** adj_lists = (Node**) calloc (g.v, sizeof(Node*));
// Set them to NULL initially
for (int i = 0; i < g.v; i++)
adj_lists[i] = NULL;
printf("Initialized Adjacency Lists!\n");
return adj_lists;
}
void free_list(Node* list) {
// Frees all nodes in the list, headed by 'list'
Node* temp = list;
while(temp) {
Node* rm_node = temp;
temp = rm_node->next;
rm_node->next = NULL;
free(rm_node);
}
}
void free_adj_lists(Graph g) {
// Free the adjacency matrix
if (!g.adj_lists)
return;
for (int i=0; i ", temp->vertex);
temp = temp->next;
}
printf("\n");
}
Node* create_node(int vertex) {
// Creates a LinkedList node to hold the vertex
Node* node = (Node*) calloc (1, sizeof(Node));
node->next = NULL;
node->vertex = vertex;
return node;
}
void add_edge(Graph g, int i, int j) {
// Adds an edge connecting two vertices i and j
if (!g.adj_lists) {
fprintf(stderr, "Adjacency Lists not initialized!\n");
exit(1);
}
else if (i > g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
exit(1);
}
// Create the new node in the souce vertex
// adjacency list and add the destination
// vertex to it
// Create a node containing the dst vertex index
Node* node = create_node(j);
// Insert at the source list
// Let's insert at the top, since it doesn't
// matter whether we insert at the head or not
node->next = g.adj_lists[i-1];
// Make the new node as the head
g.adj_lists[i-1] = node;
}
void remove_edge(Graph g, int i, int j) {
// Sets the edge from i to j as zero
if (!g.adj_lists) {
fprintf(stderr, "Adjacency Lists not initialized!\n");
exit(1);
}
else if (i > g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
exit(1);
}
// Search for vertex j in i's adjacency list
Node* temp = g.adj_lists[i-1];
if (!temp) {
return;
}
if (!(temp->next)) {
if (temp->vertex == j) {
free(temp);
g.adj_lists[i-1] = NULL;
}
return;
}
while (temp->next) {
if (temp->vertex == j) {
// We have found an edge! Remove this element.
Node* rm_node = temp;
temp->next = rm_node->next;
rm_node->next = NULL;
free(rm_node);
return;
}
temp = temp->next;
}
// No element found :(
return;
}
int check_if_exists(Graph g, int i, int j) {
// Checks if there is an edge from vertex i to j
if (!g.adj_lists) {
fprintf(stderr, "Adjacency Lists not initialized!\n");
exit(1);
}
else if (i > g.v || j > g.v) {
fprintf(stderr, "Invalid Vertex Number\n");
return 0;
}
// Search for vertex j in i's adjacency list
Node* temp = g.adj_lists[i-1];
if (!temp) {
return 0;
}
if (!(temp->next)) {
if (temp->vertex == j) {
return 1;
}
return 0;
}
while (temp->next) {
if (temp->vertex == j) {
// We have found an edge! Remove this element.
return 1;
}
temp = temp->next;
}
// No element found :(
return 0;
}
int main() {
// Graph with 4 vertices
Graph g = {4, NULL};
printf("Created a Graph Structure with %d vertices\n", g.v);
g.adj_lists = init_adjacency_lists(g);
// Let's connect the 4 vertices using edges
add_edge(g, 1, 2);
add_edge(g, 2, 1);
add_edge(g, 2, 3);
add_edge(g, 2, 4);
add_edge(g, 3, 1);
add_edge(g, 4, 3);
// Check if the edge is connected
printf("Is there an edge from 1 to 2?\n");
if (check_if_exists(g, 1, 2))
printf("Yes\n");
else
printf("No\n");
printf("Is there an edge from 4 to 3?\n");
if (check_if_exists(g, 4, 3))
printf("Yes\n");
else
printf("No\n");
printf("Is there an edge from 1 to 3?\n");
if (check_if_exists(g, 1, 3))
printf("Yes\n");
else
printf("No\n");
printf("\nPrinting the Adjacency Lists for every Vertex:\n");
for (int i=0; i Output
输出量
Created a Graph Structure with 4 vertices
Initialized Adjacency Lists!
Is there an edge from 1 to 2?
Yes
Is there an edge from 4 to 3?
Yes
Is there an edge from 1 to 3?
No
Printing the Adjacency Lists for every Vertex:
Vertex: 1 , Node: 2 ->
Vertex: 2 , Node: 4 -> Node: 3 -> Node: 1 ->
Vertex: 3 , Node: 1 ->
Vertex: 4 , Node: 3 ->
结论 (Conclusion)
With that, we have covered the basics of Graph Theory. In the upcoming articles, we will take a look at how we can solve different graph theory problems and their implementation in C.
到此为止,我们已经涵盖了图论的基础知识。 在接下来的文章中,我们将研究如何解决不同的图论问题及其在C语言中的实现。
In the meantime, do go through our latest C Programming articles, which cover differ aspects of C.
同时,请阅读我们最新的C编程文章 ,其中涵盖了C的不同方面。
参考资料 (References)
- Wikipedia Article on Graph Theory 维基百科有关图论的文章
- KhanAcademy topic on representing Graphs (Recommended Read) KhanAcademy有关表示图的主题 (推荐阅读)
翻译自: https://www.journaldev.com/35844/graph-theory-basics
图论基础知识