第16课-位运算

为什么需要位运算

• 机器里的数字表示方式和存储格式就是 二进制
• 十进制 <—> 二进制 : 如何转换?

如何从十进制转换为二进制

4(d): 0100 
8(d): 01000 
5(d): 0101 
6(d): 0110

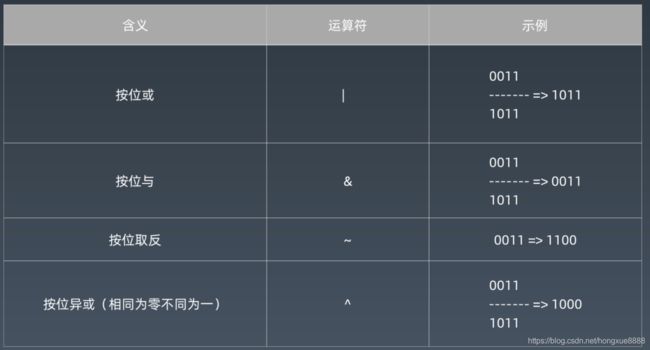
位运算符

含义	运算符	示例
左移	<<	0011 => 0110
右移	>>	0110 => 0011

32位CPU — 指的是该CPU在单位时间内能一次处理的二进制数的位数为32位，即一次处理4个字节。
64位CPU — 指的是该CPU在单位时间内能一次处理的二进制数的位数为64位，即一次处理8个字节。

位=bit，代表0或1， 比如 0000，代表4位，00001111代表8位

字节=byte=B=8bit ，一个字节就是8位

---

XOR - 异或

异或:相同为 0，不同为 1。也可用“不进位加法”来理解。

异或操作的一些特点:

x ^ 0 =x
x ^ 1s = ~x // 注意 1s = ~0
x ^ (~x) = 1s
x ^ x= 0
c = a ^ b => a ^ c = b, b ^ c = a // 交换两个数
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c// associative

指定位置的位运算

1. 将 x 最右边的 n 位清零:x & (~0 << n)
2. 获取 x 的第 n 位值(0 或者 1): (x >> n) & 1
3. 获取 x 的第 n 位的幂值:x & (1 << (n -1))
4. 仅将第 n 位置为 1:x | (1 << n)
5. 仅将第 n 位置为 0:x & (~ (1 << n))
6. 将 x 最高位至第 n 位(含)清零:x & ((1 << n) - 1)
7. 将第 n 位至第 0 位(含)清零:x & (~ ((1 << (n + 1)) - 1))

实战位运算要点

• 判断奇偶:
  x % 2 == 1 —> (x & 1) == 1
  x % 2 == 0 —> (x & 1) == 0

• x >> 1 —> x / 2
  即: x = x / 2; —> x = x >> 1;
  mid = (left + right) / 2; —> mid = (left + right) >> 1;

• X = X & (X-1) 清零最低位的 1

• X & -X => 得到最低位的 1

• X & ~X => 0

实战题目

https://leetcode-cn.com/problems/number-of-1-bits/
https://leetcode-cn.com/problems/power-of-two/
https://leetcode-cn.com/problems/reverse-bits/
https://leetcode-cn.com/problems/n-queens/description/ https://leetcode-cn.com/problems/n-queens-ii/description/

N皇后的位运算解法

• Python

def totalNQueens(self, n):
    if n < 1: return []
    self.count = 0
    self.DFS(n, 0, 0, 0, 0)
    return self.count
def DFS(self, n, row, cols, pie, na):
    # recursion terminator
    if row >= n:
        self.count += 1
        return
bits=(~(cols|pie|na))&((1<<n)—1) # 得到当前所有的空位 while bits:
p = bits & —bits # 取到最低位的1
bits = bits & (bits — 1) # 表示在p位置上放入皇后
self.DFS(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1)
# 不需要revert cols, pie, na 的状态

• Java

 Java
    class Solution {
      private int size;
      private int count;
      private void solve(int row, int ld, int rd) {
        if (row == size) {
count++;
return; }
        int pos = size & (~(row | ld | rd));
        while (pos != 0) {
          int p = pos & (-pos);
          pos -= p; // pos &= pos - 1;
          solve(row | p, (ld | p) << 1, (rd | p) >> 1);
} }
      public int totalNQueens(int n) {
        count = 0;
        size = (1 << n) - 1;
        solve(0, 0, 0);
        return count;
      }
}

DP + 位运算

LeetCode 338:
https://leetcode-cn.com/problems/counting-bits/description/

代码

vector<int> countBits(int num) {
 vector<int> bits(num+1, 0);
 for (int i = 1; i <= num; i++) {
   bits[i] += bits[i & (i — 1)] + 1;
 }
 return bits;
}