这就是贝叶斯---从数学基础到贝叶斯理论到实践
贝叶斯网络(Bayesian network)又被称为信念网络( Belief network),是一种通过有向无环图( Directed acyclic graph, DAG)表示一组随机变量及其条件依赖概率的概率图模型。在概率图中,每个节点表示一个随机变量,有向边表示随机变量之间的依赖关系,两个节点若无连接则表示它们是相互独立的随机变量。用条件概率表示变量间依赖关系的强度,无父节点的节点用先验概率表达信息。
贝叶斯网络中的节点可以表示任意问题,丰富的概率表达能力能较好地处理不确定性信息或问题。贝叶斯网络中所有节点都是可见的,并且可以非常直观地观察到节点间的因果关系。这些特性都使得贝叶斯网络在众多智能系统中有重要的应用。
贝叶斯理论概述
随着人工智能的发展,对贝叶斯网络的理论研究愈加广泛,研究领域涵盖了网络的结构学习、参数学习、因果推理、不确定知识表达等
贝叶斯方法的特点是用概率表示不确定性,概率规则表示推理或学习,随机变量的概率分布表示推理或学习的最终结果。
贝叶斯理论源于贝叶斯提出的贝叶斯定理和贝叶斯假设。
贝叶斯定理引入了先验概率(指根据以往经验和分析得到的概率),后验概率由先验概率和类条件概率表达式计算出。假设有随机变量x和y, p ( x , y ) p(x, y) p(x,y)表示它们的联合概率, p ( x l y ) p(xly) p(xly)和 p ( y ∣ x ) p(y|x) p(y∣x)表示条件概率,其中 p ( y ∣ x ) p(y|x) p(y∣x)是后验概率,而p(y)称为y的先验概率,x和y的联合概率和条件概率满足下列关系 p ( y , x ) = p ( y l x ) p ( x ) = p ( x ∣ y ) p ( y ) p(y,x)=p(ylx)p(x)=p(x|y)p(y) p(y,x)=p(ylx)p(x)=p(x∣y)p(y)交换后得到: p ( y ∣ x ) = p ( x ∣ y ) P ( y ) / p ( x ) p(y|x)=p(x|y)P(y) /p(x) p(y∣x)=p(x∣y)P(y)/p(x)
上述公式即为贝叶斯定理

贝叶斯假设:如果没有任何已有的知识来帮助确定先验概率p(y),贝叶斯提出使用均匀分布作为其概率分布,即随机变量在其变化范围内取为各个值的概率是一定的
贝叶斯概率基础
概率论
若在大量重复实验中,事件x发生的频率稳定地接近一个固定常数p, 则p称为事件x发生的概率,记为p(x)。(0 古典概率:设一种实验有且仅有有限的n个可能结果,即有n个基本事件,而x事件包含着m个可能结果,则称m/n为事件x的概率,记为P(x)=m/n 乘法定理: x, y两个不相容非零事件,-其乘积的概率等于x和y概率的乘积,即p(x,y)=p(x)p(y) 独立事件: x,y两个事件,若任一事件发生与否不影响另一个事件发生的可能性,则称x与y是相互独立的事件 联合概率分布:单随机变量x的概率分布可用p(x)表示,对多个随机变量X1,X2…Xn可用联合概率分布p(X1,X2,…,Xn),即联合分布来描述各个变量所有可能的状态组合的概率。其中所有状态函数值之和为1,即有 先验概率:在实验前根据以往的数据分析得到的事件发生概率。 后验概率:利用贝叶斯定理和实验的信息对先验概率做出修正后的概率。 全概率公式:设 y 1 , y 2 , . . y n y_1, y_2, .. y_n y1,y2,..yn,是两两互斥的事件,且 p ( y i ) > 0 , i = 1 , 2 , . . . . n , y i ∈ Ω p(y_i)>0, i=1, 2,....n, y_i∈\Omega p(yi)>0,i=1,2,....n,yi∈Ω另有一事件 x = x y 1 + x y 2 + . . . + x y m x=xy_1+xy_2+ ...+xy_m x=xy1+xy2+...+xym;则有 p ( x ) = ∑ i p ( x ∣ y i ) p ( y i ) p(x)= \sum_{i}{p(x|y_i)}{p(y_i)} p(x)=∑ip(x∣yi)p(yi)可以将 y i y_i yi视作原因,x视作结果,结果的发生有多种原因。 贝叶斯公式:假设x和y分别是样本属性和类别,p(x, y)表示它们的联合概率, p ( x ∣ y ) p(x|y) p(x∣y)和 p ( y ∣ x ) p(y|x) p(y∣x)表示条件概率,其中 p ( y ∣ x ) p(y|x) p(y∣x)是后验概率,而p(y)为y的先验概率,x,y的联合概率和条件概率满足: p ( x , y ) = p ( y ∣ x ) p ( x ) = p ( x l y ) p ( y ) p(x, y)=p(y|x)p(x)=p(xly)p(y) p(x,y)=p(y∣x)p(x)=p(xly)p(y)变换后得到贝叶斯公式: 上述公式称为贝叶斯定理,它提供了从先验概率p(y)计算后验概率p(y|x)的方法。在样本分类时,利用训练样本可以计算出不同类别的后验概率。例如类别y;的先验概率为p(y),实验所得的新信息为 后验概率$p(y_i|x_i)最大的类别y;可以作为样本的分类。 男生总是穿长裤,女生则一半穿长裤一半穿裙子 假设学校里面人的总数是 U 个 求解:穿长裤的人里面有多少女生 P ( G i r l ∣ P a n t s ) = U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) 穿 长 裤 总 数 = U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) [ U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) ] P(Girl|Pants) = \frac{U * P(Girl) * P(Pants|Girl)}{穿长裤总数}=\frac{U * P(Girl) * P(Pants|Girl)} { [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)]} P(Girl∣Pants)=穿长裤总数U∗P(Girl)∗P(Pants∣Girl)=[U∗P(Boy)∗P(Pants∣Boy)+U∗P(Girl)∗P(Pants∣Girl)]U∗P(Girl)∗P(Pants∣Girl) 与总人数有关吗? U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) \frac{U * P(Girl) * P(Pants|Girl)} {U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)} U∗P(Boy)∗P(Pants∣Boy)+U∗P(Girl)∗P(Pants∣Girl)U∗P(Girl)∗P(Pants∣Girl) 容易发现这里校园内人的总数是无关的,可以消去 化简: p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) p(y|x)=\frac{p(x|y)p(y)}{p(x)} p(y∣x)=p(x)p(x∣y)p(y) 朴素贝叶斯分类模型是一种简单的构造分类器的方法。朴素贝叶斯分类模型将问题分为特征向量和决策向量两类,并假设问题的特征变量都是相互独立地作用于决策变量的,即问题的特征之间都是互不相关的。朴素贝叶斯分类模型能指数级降低贝叶斯网络构建的复杂性,同时还能较好地处理训练样本的噪声和无关属性,所以朴素贝叶斯分类模型仍然在很多现实问题中有着高效的应用,例如入侵检测和文本分类等领域。 假设问题的特性向量为 X = X 1 , X 2 , . . , X n X={X1,X2,..,Xn} X=X1,X2,..,Xn,并且 X 1 , X 2 , . . X n X1,X2,.. Xn X1,X2,..Xn之间相互独立,那么 p ( x ∣ y ) p(x|y) p(x∣y)可以分解为多个向量的积,即有 (2)对于连续性的特征属性x;通常先将x;离散化,然后计算属于类y的训练样本落在x;对应离散区别的比例估计p(x;/Y)。也可以假p(x;/Y)的概率分布,如正态分布,然后用训练样本估计其中的参数。 (3)而在p(x;/Y)=0的时候, 该概率与其他概率相乘的时候会把其他概率覆盖,因此需要引入Laplace修正。做法是对所有类别下的划分计数都加一,从而避免了等于零的情况出现,并且在训练集较大时,修正对先验的影响也会降低到可以忽略不计。 综合上述分析,可以归纳出朴素贝叶斯分类模型应用流程的三个阶段,如图所示。 ①准备阶段。这阶段主要是对问题进行特征提取,建立问题的特征向量,并对其进行一定的划分形 成训练样本,这些工作主要由人工完成,完成质量对整个分类器的质量有着决定性影响。 ②)训练阶段。根据上述分析中的公式计算每个类别在训练样本中的出现频率,以及每个特征对每个类别的条件概率,最终获得分类器。 ③应用阶段。该阶段会将待分配项输入分类器中,利用上述的公式自动进行分类。 朴素贝叶斯分类器还可以进行提升( Boosting)。提升方法中关键一步是数据训练集的权重调整过程,权重调整可以通过两种方法实现,分别为重赋权法和重采样法。重赋权法对每个训练集的样本添加一个权重,对于离散型的特征 x i x_i xi而言,计算条件概率 p ( x i ∣ y ) p(x_i|y) p(xi∣y)时不再是直接计次,而是对样本的权重进行累加;对于连续性的特征 x i x_i xi权重改变表现为均值的偏移,因此可以通过增大或减小连续属’性的值来达到赋权的目的。重采样法适用于不能给样本添加权值的情况。由于初始时是根据相同的概率从训练集中采集数据,现在可以通过权重来调整采集的概率,每次在学习一个分类器错误的训练数据后,后一-个分类器可以根据新的调整后的概率重新在训练样本中采集数据。值得注意的是,由于朴素贝叶斯分类器是基于数据统计的分类器,先验概率预先确定,仅仅通过调整训练样本选择的权重对朴素贝叶斯分类的提升效果并不明显。提升方法更常用于决策树、神经网络等分类器中。 拼写纠正实例: 问题是我们看到用户输入了一个不在字典中的单词(比如the 写成了tha),我们需要去猜测:“这个家伙到底真正想输入的单词是什么呢? 假设用户实际输入的单词记为 D ( D 代表 Data ,即观测数据) 猜测1:P(h1 | D),猜测2:P(h2 | D),猜测3:P(h1 | D) 。。。(h123…都是猜测数据) P ( h ∣ D ) = P ( h ) ∗ P ( D ∣ h ) P ( D ) P(h | D) =\frac{ P(h) * P(D | h)}{ P(D)} P(h∣D)=P(D)P(h)∗P(D∣h) 对于不同的具体猜测 h1 h2 h3 … ,P(D)都是一样的,所以在比较P(h1 | D) 和 P(h2 | D) 的时候我们可以忽略这个常数 对于不同的具体猜测 h1 h2 h3 … ,P(D) 都是一样的,所以在比较P(h1 | D) 和 P(h2 | D) 的时候我们可以忽略这个常数 贝叶斯方法计算: P(h) * P(D | h),P(h) 是特定猜测的先验概率比如用户输入tlp ,那到底是 top 还是 tip ?这个时候,当最大似然不能作出决定性的判断时,先验概率就可以插手进来给出指示——“既然你无法决定,那么我告诉你,一般来说 top 出现的程度要高许多,所以更可能他想打的是 top ” 还有拼错检查和文本分析源码在这里
几何概率:设几何概率:设 Ω \Omega Ω是几何型随机实验的基本事件空间,在 Ω \Omega Ω中进行等可能的投点,点落在某一区域x的概率p(x)与该区域的面积S、成正比,有 p ( x ) = S x / S Ω p(x)=S_x/S_\Omega p(x)=Sx/SΩ, 其中 S Ω S\Omega SΩ表示整个区域的面积。
条件概率:设x,y是两个事件,且p(x)>0,称p(y|x)=p(xy)/p(x)
为事件x发生的条件下事件y发生的条件概
率。
加法定理: x, y两个不相容事件之和的概率,等于两个事件概率之和,即p(x+y)=p(x)+p(y)
条件概率分布:设随机变量x和y,在x=X, y=Y时有条件概率为 p ( x = X ∣ y = Y ) = p ( x = X , y = Y ) p ( y = Y ) p(x=X|y=Y)=\frac{p(x=X,y=Y)}{p(y=Y)} p(x=X∣y=Y)=p(y=Y)p(x=X,y=Y)上式中固定y,则x在定义域上的不同取值X可得到在x定义域上的函数,该函数即称为给定y=Y时随机变量x的条件概率分布。贝叶斯概率
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) p(y|x)=\frac{p(x|y)p(y)}{p(x)} p(y∣x)=p(x)p(x∣y)p(y)
p ( x j l y i ; ) ( i = 1 , 2 , . . . m ; j = 1 , 2 , . . . n ) p(x_jly_i;) (i=1,2,...m;j=1, 2,...n) p(xjlyi;)(i=1,2,...m;j=1,2,...n),则计算样本x;属于类别y;的后验概率:

该公式还可以表示在事件x已经发生的条件下,找到导致x发生的各个原因的概率。上面是不是有点懵,来看个小例子吧!!
正向概率:随机选取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大
逆向概率:迎面走来一个穿长裤的学生,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别,你能够推断出他(她)是女生的概率是多大吗?
穿长裤的(男生): U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) U * P(Boy) * P(Pants|Boy) U∗P(Boy)∗P(Pants∣Boy)
P(Boy) 是男生的概率 = 60%
P(Pants|Boy) 是条件概率,即在 Boy 这个条件下穿长裤的概率是多大,这里是 100% ,因为所有男生都穿长裤
穿长裤的(女生): U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) U * P(Girl) * P(Pants|Girl) U∗P(Girl)∗P(Pants∣Girl)
穿长裤总数: U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) U∗P(Boy)∗P(Pants∣Boy)+U∗P(Girl)∗P(Pants∣Girl)
P ( G i r l ∣ P a n t s ) = P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) P(Girl|Pants) = \frac{P(Girl) * P(Pants|Girl) }{P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)} P(Girl∣Pants)=P(Boy)∗P(Pants∣Boy)+P(Girl)∗P(Pants∣Girl)P(Girl)∗P(Pants∣Girl)
P ( G i r l ∣ P a n t s ) = P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) = P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) P ( P a n t s ) P(Girl|Pants) =\frac{P(Girl) * P(Pants|Girl)} {P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)} =\frac{P(Girl) * P(Pants|Girl)} {P(Pants)} P(Girl∣Pants)=P(Boy)∗P(Pants∣Boy)+P(Girl)∗P(Pants∣Girl)P(Girl)∗P(Pants∣Girl)=P(Pants)P(Girl)∗P(Pants∣Girl)
分母其实就是 P(Pants)朴素贝叶斯分类模型

那么这个问题就可以由朴素贝叶斯分类器来解决,即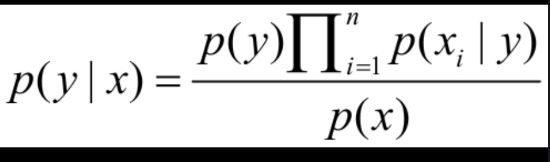
其中p(x)是常数,先验概率p(y)可以通过训练集中每类样本所占的比例进行估计。给定Y=y,如果要估计测试样本x的分类,由朴素贝叶斯分类得到y的后验概率为:

因此最后只要找到使![p(y=Y)]I _P(x,|y=Y)](http://img.e-com-net.com/image/info8/71e0eac384704f6c971ac69d3dd6dd54.jpg) 最大的类 别y即可。
最大的类 别y即可。
从计算分析中可见, p ( x i ∣ y = Y ) p(x_i|y= Y) p(xi∣y=Y)的计算是模型关键的一步,这一步的计算视特征属性的不同也有不同的计算方法。
( 1 )对于离散型的特征属性x;,可以用类y中的属性值等于x;的样本比例来进行估计。
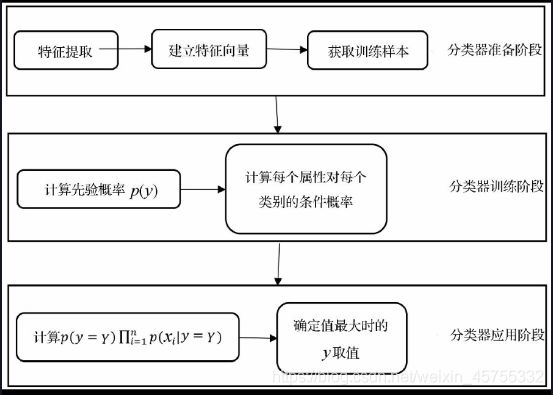
朴素贝叶斯分类模型结构简单。由于特征变量间的相互独立,算法简单易于实现。同时算法有稳定的分类效率,对于不同特点的数据集其分类性能差别不大。朴素贝叶斯分类在小规模的数据集.上表现优秀,并且分类过程时空开销小。算法也适合增量式训练,在数据量较大时,可以人为划分后分批增量训练。
需要注意的是,由于朴素贝叶斯分类要求特征变量满足条件独立的条件,所以只有在独立性假定成立或在特征变量相关性较小的情况下,才能获得近似最优的分类效果,这也限制了朴素贝叶斯分类的使用。朴素贝叶斯分类需要先知道先验概率,而先验概率很多时候不能准确知道,往往使用假设值代替, 这也会导致分类误差的增大。是不是又有点懵呢?再来看例子!!!
下面做一些猜测:
统一为:P(h | D)
P(h | D)=P(我们猜测他想输入的单词 | 他实际输入的单词)
P(h)是先验概率,如某个词在语料库的概率是多少,我们是已经提前知道的
P(D)是可以约掉的
P(h | D) ∝ P(h) * P(D | h)(正比)对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior )”和“这个猜测生成我们观测到的数据的可能性大小,也就是the写成tha的可能性大小。
P(h | D) ∝ P(h) * P(D | h)
对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior )”和“这个猜测生成我们观测到的数据的可能性大小。