图论总结(一)
写在前面的话
偶尔出来发个大招
谨以此篇献给我最爱的grandpa, 你知道的没有你就没有我。我觉得我对你说我爱你说的太少了。只有你会在我发烧时候每隔5分钟来摸摸我的脑袋。为我跑遍整个昆明城买我最喜欢的食物,为我跑遍整个昆明城帮我办公交卡,在我人生低谷,不吃不喝的时候濒临奔溃的时候一直安安静静的陪我哭,帮我想办法,让我活过来。只有你,会为我剪报纸,帮我搜集高考每一所学校的录取学校,做成美美的小册子。我上班太辛苦了,你总是说宝宝,我们家不缺钱,不用这么拼,外公养你一辈子,你在家给我做做饭就够了,钱够花就行。我初中赖床,不起床复习,你总是把我吼起来,你说你看看你上次年纪第三,这次考第五,都下降了,咱们能严格要求下自己么。我上班起不来,我叫你叫我起床,你说几点,我说8点,你总是说让你没有成就感,哪有人8点还要人叫起床的。我出国交流,回家躺倒床上就睡,你总是提着拖把闯进来,把我拎起来,问我为什么还不复习雅思。为什么不好好准备考试。我每次躺倒床上没几分钟,你就过来闹觉,我每次都是装作听不见。谢谢你在初中的时候一直教我电路图,我们一起做插座,一起动手安装家具,我们一起卖废品,一起收集瓶子,一起卖废报纸,一起去购物,你总是喜欢坐在超市的沙发上享受一会。你喜欢偷怕我和外婆。所以我叫你冠希哥。我总是用脚戳你,你一趟在沙发上。你总是倔强,不许我乱花钱,自己动手做床。我们一起种了树,很多树,家里很美,我们种了很多花。你帮我做镜子,还把我小学二年级的照片黏在后面,我说干嘛要粘这么马肯头的一张,你说,我孙女是全世界最美的。我用你手机照了一张相,你见人就炫耀,你看,我孙女是不是全世界最美的小姑娘,这么标志,简直是遗传外婆的所有优点。哪有小孩子5岁都不断奶,因为都是你惯的,你每天晚上都要给我起来煮奶。我们一起吹泡泡,一起喂鸡,我帮你洗你的臭袜子,你背着我每周二去集市买大白兔,搞的我一口虫牙。你每天吃饭都会出脑筋急转弯给我。你说我们这臭脾气很像,对呀,我不像你像谁,我是你骄傲,这么会这么轻易让人超越。我们一直就是这么霸气侧漏,我们不用逼自己变优秀。你跟我开家长会总是在拉自己的胡子。哈哈,你还从床上睡到掉下来,你真的好笨!
我知道的血液就是你血脉的延续,所以我做每一件事都是你的标识。我会把我做的每一件事情都做到极致,跟自己约定,等明年的时候,我会在全球最好的会议上亲自告诉最顶尖的科研人员,我会做最好的研究,用最踏实的态度活好每一天,那是因为你。
你说如果你接受和我一样的教育,你会成为比我厉害一百倍的科学家,我说,你会。我跟你开玩笑说,外公,你这么厉害,你一定能比屠呦呦厉害。以后我们家都靠你养了,你也去发明个什么青蒿素,完全不是问题。
外公,我要让全世界看见,你的血液里面最闪光的所有宝藏。I promise。在我心跳停止的之前,我会努力做到让全世界为你致敬,把你所有美好的品质发挥到极致。
你说的,我是你的骄傲,我会一直是你最好的骄傲。always and forever, we are family, I love you, always and forever.
我说你是全世界最聪明的老爷爷,你这么努力,你这么能干,你是我的骄傲,我会加油。你要好好照顾自己,I miss you.
感觉自己真的很任性,一次一次说我是为自己的梦想,每次都不顾一切不考虑你的年纪,让我比同龄人慢了很多,你总是这么倔,你就为给我省钱不好好照顾自己。我自己也不好,没有固执的带你去看医生,没有固执给你买我所有想买给你的东西。你总是嫌我品味差,给你买的鞋子难看。给你买的皮鞋你一次都没有穿过。
对不起,对不起,对不起。我这么不好,我这么不好,固执,倔强,蛮横,执拗,你还是这么一直一直很好很好的给我全世界最好的爱。感觉自己欠了外公10年的时光。我会努力,明年我就在家里最好的地方买一幢别墅给外婆,不用让你再去爬楼梯,我会给你买最好的地方,让你可以每天可以看到八百里滇池的日出日落,每天都可以吹吹海风。
我们一直是家人对不对,I love you.
好像图论和树在计算机的数据结构中,都有种魔咒,好难,代码也不好写。我觉得难的是心态,要是预先给我们自己定了一个这个东西很难的调调,然后我们永远做不好这事。只要用心,没有什么是我们不可以实现的,我们做的每一件事就是为了创造奇迹而存在的。这是我外公教我的,他每天都是这么实践的。
图的定义
图(graph)G=(V,E)由顶点(vertex)的集V和边(Edge)的集E组成。顶点代表了对象,在示意图中我们使用点或圆来表示它;边代表了两个对象的连接关系,在示意图中我们使用连接两顶点的线段来表示。
有时也把边称作弧(arc),如果点对(v,w)是有序的,那么图就叫做有向的图(有向图)。如果点对(v,w)是无序的,那么图就叫做无向的图(无向图)。简单的讲,边没有指向性的图叫做无向图,边具有指向性的图叫做有向图。
顶点v和w邻接(adjacent)当且仅当(v,w)属于E。
我们可以给边赋予各式的属性,比如权值(cost)。权值可以表示从一个顶点到另一个顶点的距离,也可以表示一个顶点到另一个顶点说话费的代价(比如时间、金钱等)。一个边上带权值的图称为网络(network)。
如果无向图中从每一个顶点到其他每个顶点都存在一条路径,则称该无向图是连通的(connected)。具有这样性质的有向图称为是强连通的的(strongly connected)。如果有向图不是强连通的,但它的基础图(underlying graph)(也就是其弧上去掉方向说形成的图)是连通的,那么称该有向图是弱连通的(weakly connected)。完全图(complete graph)是其每一对顶点间都存在一条边的图。
度(degree)指的是顶点v的边的条数。
如果具有n个顶点,e条边的图G的顶点i的度为di,则G的边数为:
$ e =\frac { \sum_{0}^{n-1} d_i} {2} $
这个是针对无向图来说的。
我们给每个节点编号
刚好是7。这个高中的时候学欧拉公式应该很熟练了(新教材被删减了,我又暴露年龄了),因为针对每一条边,它的每天边被每个顶点重复利用了一次。对于边1-2和变2-1其实是相同的事情。
所以在这里我们是需要除以二的。
但是对于有向图,我们只需要计算每个顶点的出度或者是入度就可以知道这个图总共是有多少条边。
这《数据结构与算法C语言版》的这本书中这个比较经典的图形,我们计算这个图形的边,同样可以先把它看成是无向图。按照上面的公式来计算:
又或者你可以根据这个图的出度或者是入度中的任意一个来计算,下面我们选择的是出度来计算这个有向图的边。
图的存储表示方式
图主要有3种常用的存储表示方式:邻接矩阵(adjacency matrices),邻接表(adjacency lists),邻接多重表(adjacency multilists)
##邻接矩阵
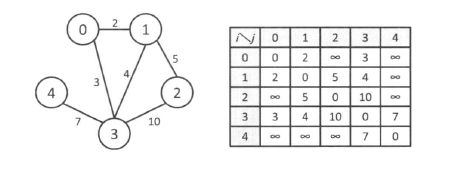
邻接矩阵使用|V|∗|V|的二维数组来表示图。g[i][j]表示的是顶点i和顶点j的关系。
1)因为在无向图中,我们只需要知道顶点i和顶点j是否是相连的,因此我们只需要将g[i][j]和g[j][j]设置为1或是0表示相连或不相连即可。如下图所示。
2)而在有向图中,我们只需要知道是否有从顶点i到顶点j的边,因此如果顶点i有一条指向顶点j的边,那么g[i][j]就设为1,否则设为0。有向图与无向图不同,并不需要满足g[i][j]=g[j][i]。
3)在带权值的图中,g[i][j]表示的是顶点i到顶点j的边的权值。由于在边不存在的情况下,如果将g[i][j]设为0,就无法和权值为0的情况区分开来,因此选取适当的较大的常数INF(只要能和普通的权值区别开来就可以了),然后令g[i][j]=INF就好了。当然,在无向图中还是要保持g[i][j]=g[j][i]。在一条边上有多种不带权值的情况下,定义多个同样的|V|∗|V|数组,或者是使用结构体或类作为数组的元素,就可以和原来一样对图进行处理了。
使用这种存储方式,可以很方便地判断任意两个顶点之间是否有边以及确定顶点的度,这也是这种表示法最大的优势。任意一个顶点i的度等于其邻接矩阵中顶点i所对应的行中的数字之和:
$ \sum_{j=0}^{n-1} g[i][j] $
在这种表示法中扫描所有边至少需要O(n2)时间,因为必须检查矩阵中的n2−n个元素才能确定图中边的条数(邻接矩阵对角线上的n个元素都是0,因此不用检查。又因为无向图的邻接矩阵是对称的,实际只需检查邻接矩阵的一半元素)。通常把边很少的图成为稀疏图(sparse graphs)
图的同构
我们先看一个简单的例子:
对于上面这个简单图,我们用邻接矩阵来表示这个图,得到的形式如下所示:
- 首先,我们需要明确一点,图的邻接矩阵是不唯一,取决于顶点的排列顺序.
- 无向图的邻接矩阵是对称的
定义
同构的图:本质上相同的图,表示了类似的集合和关系
函数f满足f(u1)=v1,f(u2)=v4 ,f(u3)=v3 ,f(u4)=v2 ,它是V和W之间的一一对应。为了看出这个对应保持相邻关系,注意G里相邻的顶点是u1和u2, u1和u3,u2和u4,以及u3和u4,由f(u1)=v1和f(u2)= v4 ,f(u1)=v1 和f(u3)= v3 ,f(u2)= v4和f(u4)= v2 ,以及f(u3)= v3和f(u4)= v2所组成的每一对顶点都是在H里相邻的。
图的同构是一个一一对应关系,但是子图同构在严格的意义上讲不能叫做映射。
why?
我们先说明完图的同构问题.
同构的充分条件,可用于判定同构
给出一个顶点的一一对应,按相应的顺序求出邻接矩阵
邻接矩阵相同 ==》那么图是同构
同构的必要条件,可用于判定不同构
(1)顶点数相同
(2)边数相同
(3)顶点度相同
(4)同度顶点构成的子图都同构
G和H都具有5个顶点和6条边。不过,H有1度顶点e而G没有1度顶点。
我们可以看出在H这个图中节点e只有一个度,在图G中我们根本找不到节点的度是1的。
所以G与H是不同构的。
重要的事情多说几遍,我们判断两个图是不是同构的,可以根据节点的度来判断 .
图G和H都具有8个顶点和10条边。它们都具有4个2度顶点和4个3度顶点。因为这些不变量都相同,所以可能想到它们是同构的.
然而G和H不是同构的。为了看明白这一点,注意到因为在G里deg(a)=2,所以a必然对应于H里的t,u,x或y,这是因为这些顶点是H里的2度顶点。不过, H里的这4个顶点中每一个都与H里另一个2度顶点相邻,但是在H里a却不是这样的。
图同构的,那么度相同的节点构成的子图也是同构的。
我们看一下这两个图中度为三的节点构成的子图是什么样子的:
如下图所示:
根据上图所示,这两个图明显是不同构。
今天先写到这,下次写图同构算法。现在回去写代码,论文要写,代码要写,事情很多,算法要看,学习要学。
无意中发现了一个巨牛的人工智能教程,忍不住分享一下给大家。教程不仅是零基础,通俗易懂,而且非常风趣幽默,像看小说一样!觉得太牛了,所以分享给大家。点这里可以跳转到教程 https://www.cbedai.net/chichoxian
我们习惯那些旧时光叫做那年夏天
我想念那篇花海的樱顶和老图,早上六点的那些屋檐
还有旧旧的数学学院
和chuanbo一起在信操的足球赛大罐大罐喝啤酒看月亮的日子
和兔兔一起奋斗的日子
炎热的夏天,旧旧破破的图书馆,YJ和我一起埋头学习的日子。那些旧时光
坐在双层大巴上,和奇奇一起游玩的日子,我们一起聊着周杰伦的《你听得到》的MV
西瓜的味道,米饭的香味,我走在走廊写代码熬夜看Android系统代码的日子。
不顾一切爱一个人的日子
谢谢自己没有被这个世界磨平
chathrine 问我,如果有一个男生不喜欢自己,还会每天在他的桌子上放一个苹果么,这么傻傻的付出。我回答:当然会。
他们问我你还相信你会改变世界么,我回答:当然会。
你看,我现在不就是在做这件事情么。。。
我相信whu的那间教室,会一直因为我存在过书声琅琅。。。
新年愿望,可以是坏人有坏报么。哈哈,走了,旧时光