最优传输-Sinkhorn算法（第九篇）

最优传输系列是基于Computational Optimal Transport开源书的读书笔记

Sinkhorn算法

在上一篇里，我们介绍了加入熵正则化的最优传输问题–熵正则化通过限制最优传输问题解的复杂度，可以以大幅降低的复杂度得到最优传输问题的近似解。

不过，熵正则化仍然是一个概念，需要一个有效的算法，才能够释放它的潜力。
所以，在这一篇里，我们探索实际应用中十分常见的Sinkhorn算法。

得到Sinkhorn算法的第一步在于换一种方式表达正则化后的问题

正则化后的Kantorovich问题的解可以写为以下形式（4.12）：
$\forall (i,j)\in [n]\times [m],{\mathbf{P}}_{i,j}={\mathbf{u}}_i{\mathbf{K}}_{i,j}{\mathbf{v}}_j$

这里${\mathbf{K}}_{i,j}=e^{-{\mathbf{C}}_{i,j}/\epsilon }$,${\mathbf{u}}_i=e^{{\mathbf{f}}_i/\epsilon }$,${\mathbf{v}}_j=e^{{\mathbf{g}}_j/\epsilon }$
$\epsilon$是上一篇里介绍的正则化系数，控制着正则化的强度

当然，因为C矩阵是已知的，K矩阵也已知，而矢量u,v则是Sinkhorn算法需要求的变量。得到u,v也就得到了Kantorovich的对偶问题解f,g，最优传输的求解就完成了。

加入最优传输的质量守恒条件，我们得到以下两个条件
$\mathbf{u}\odot (\mathbf{K}\mathbf{v})=\mathbf{a}\text{ and }\mathbf{v}\odot \left({\mathbf{K}}^{\mathrm{T}}\mathbf{u}\right)=\mathbf{b}$

这里$\odot$是矢量的哈达马积（Hadamard product），也就是元素对应的乘积。

这一对等式已经属于一类叫做matrix scaling的数学问题，于是可以通过迭代方式求解。

每一步先更新u满足左侧等式，再更新v满足右侧等式，最终迭代收敛，两侧等式同时满足，我们就得到了最优解

${\mathbf{u}}^{(\ell +1)}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}.}{=}\frac{\mathbf{a}}{\mathbf{K}{\mathbf{v}}^{(\ell )}}\text{ and }{\mathbf{v}}^{(\ell +1)}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}.}{=}\frac{\mathrm{b}}{{\mathbf{K}}^{\mathrm{T}}{\mathbf{u}}^{(\ell +1)}}$

而基本Sinkhorn算法的初始化也十分简单：${\mathbf{v}}^{(0)}=1_m$，也就是将v中每个元素都设为1

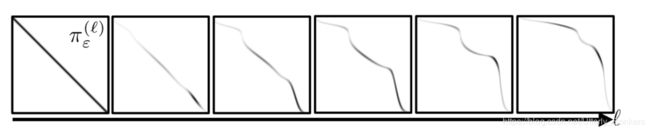图（4.5）中展示了Sinkhorn算法收敛的过程。可以清楚地看到，Sinkhorn算法从初始化状态向最优解转变。
这里图中曲线的意义可能不是非常容易理解，可以参考2.3结中更加完整的可视化
这里的曲线和图2.5中右下角是一类，代表着两个连续质量分布之间的转换。

这一节还有一个重要结论–Sinkhorn算法的复杂度
我们把正则化系数$\epsilon$写成以下的形式（$\tau$是个新的变量）：
$\epsilon =\frac{4\log (n)}{\tau }$
那么Sinkhorn可以在以下次迭代后达到原始问题最优解的近似
$O\left(\Vert \mathbf{C}{\Vert }_{\infty }^3\log (n){\tau }^{-3}\right)$，
而达到的传输代价近似误差正是$\tau$
$⟨\hat{\mathbf{P}},\mathbf{C}⟩\le {\mathrm{L}}_{\mathbf{C}}(\mathbf{a},\mathbf{b})+\tau$

由于Sinkhorn算法的复杂度十分重要，这里额外解释公式中的变量
$n$是传输维度，这里假设两个质量分布的维度均为$n$
$\Vert \mathbf{C}{\Vert }_{\infty }^3$是传输代价矩阵$\mathbf{C}$的L-infinity的三次方，可以理解为C中最大元素的绝对值的三次方
${\mathrm{L}}_{\mathbf{C}}(\mathbf{a},\mathbf{b})$是非正则化问题的传输代价
$\hat{\mathbf{P}}$是Sinkhorn求出的近似传输矩阵

有了对Sinkhorn算法的认识，我们对最优传输的了解就浅而全面了，从主要优势到算法执行都有基本的理解
下面，我们将以这个全面的认知作为地基，继续探索最优传输在当今人工智能领域中的应用