图的连通性问题

一：判断图中的俩点是否连通

     1.floyed算法: 0(N^3)

       把相连的俩点间的距离设为dis[i][j]=true,不相连的俩点设为dis[i][j]=false,用floyed算法的变形：

    

void floy()
{
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                dis[i][j]=dis[i][j]||(dis[i][j]&&dis[k][j]);
            }
        }
    }
}

   最后如果dis[i][j]=true的话，那么说明i,j俩点之间的路径连通

   有向图与无向图都使用

 

 

 2.遍历算法:0(N^2)

     主要是dfs 有向图与无向图都适用

    从任意一个顶点出发，进行一次遍历，能够从这个点出发到达的点就与起点是连通的。

   所以只要把每个顶点作为出发点都进行一次遍历，就能知道任意俩个顶点之间是否有路存在

 

 

二：最小环问题

     最小环就是指在一张图中找出一个环，使得这个环上的各条边的权值之和最小。在floyed的同时，可以顺便算出最小环算出最      小环

    记两点间的最短路径为dis[i][j],g[i][j]为边的权值

       

for(int k=1;k<=n;k++){
    for(int i=1;i<=k-1;i++){
        for(int j=i+1;j<=k-1;j++){
            answer=min(answer,dis[i][j]+g[i][k]+g[k][j]);
        }
    }
    for(int i=1;i<=n;i+){
        for(int j=1;j<=n;j++){
            dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        }
    }
}

 

 

三：求有向图的强连通分量

     因为tarjan要比Kosaraju算法要好，所以总结了tarjan算法

 

 

学习tarjan前需要掌握的知识：

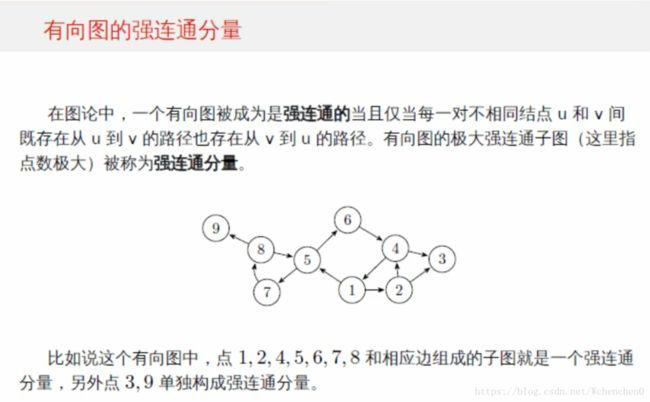
  强连通(strongly connected)： 在一个有向图G里，设两个点 a b 发现，由a有一条路可以走到b，由b又有一条路可以走到a，我                                                   们就叫这两个顶点（a，b）强连通。

  强连通图： 如果 在一个有向图G中，每两个点都强连通，我们就叫这个图，强连通图。

  强连通分量strongly connected components)：在一个有向图G中，有一个子图，这个子图每2个点都满足强连通，我们就叫这                                                                          个   子图叫做 强连通分量 （分量：把一个向量分解成几个方向的向量的和，那                                                                         些方向上的向量就叫做该向量（未分解前的向量）的分量）

 

 

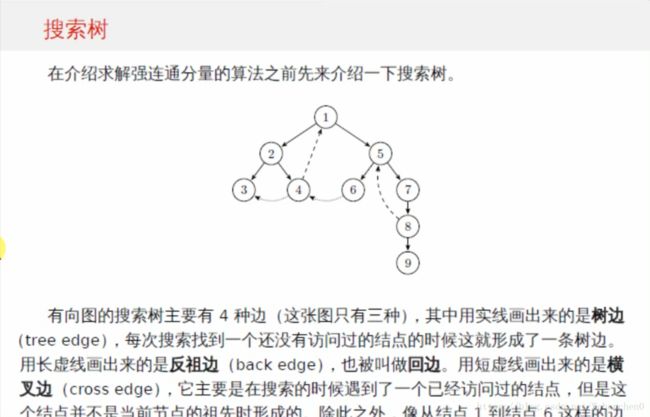
搜索树：

前向边

 

 

描述tarjan算法

理解下low ：就是存最小的时间戳

描述代码过程：

 

输入：
一个图有向图。
输出：
它每个强连通分量。

这个图就是刚才讲的那个图。一模一样。

input:

6 8

1 3

1 2

2 4

3 4

3 5

4 6

4 1

5 6

output:

6

5

3 4 2 1

 

 #include
 #include
 #include
 using namespace std;
 struct node {
     int v,next;
 }edge[1001];
  int DFN[1001],LOW[1001];
 int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y)
{
     edge[++cnt].next=heads[x];
     edge[cnt].v = y;
     heads[x]=cnt;
    return ;
 }
 void tarjan(int x)//代表第几个点在处理。递归的是点。
 {
     DFN[x]=LOW[x]=++tot;// 新进点的初始化。
     stack[++index]=x;//进站
     visit[x]=1;//表示在栈里
    for(int i=heads[x];i!=-1;i=edge[i].next)
     {
         if(!DFN[edge[i].v]) {//如果没访问过
            tarjan(edge[i].v);//往下进行延伸，开始递归
             LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
        }
        else if(visit[edge[i].v ]){  //如果访问过，并且还在栈里。
             LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
         }
     }
     if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
    {
         do{
            printf("%d ",stack[index]);
             visit[stack[index]]=0;
             index--;
         }while(x!=stack[index+1]);//出栈，并且输出。
         printf("\n");
     }
     return ;
 }
 int main()
 {
     memset(heads,-1,sizeof(heads));
     int n,m;
     scanf("%d%d",&n,&m);
    int x,y;
     for(int i=1;i<=m;i++)
     {
         scanf("%d%d",&x,&y);
        add(x,y);
     }
    for(int i=1;i<=n;i++)
         if(!DFN[i])  tarjan(i);//当这个点没有访问过，就从此点开始。防止图没走完
    return 0;
 }

 

一题基础运用tarjan的题

例题 

 

 

四：求无向图的连通分量

    并查集可以：（因为并查集是没有方向的）