BFS常见模板题（初学BFS推荐）

BFS类题目：主要考查对广度搜索的理解。

BFS相比于暴力枚举来说效率更高。
BFS只要将范围矩阵扫一次即可得出答案。
本文通过队列来实现求解，当然也可以用其他方式实现广度搜索。

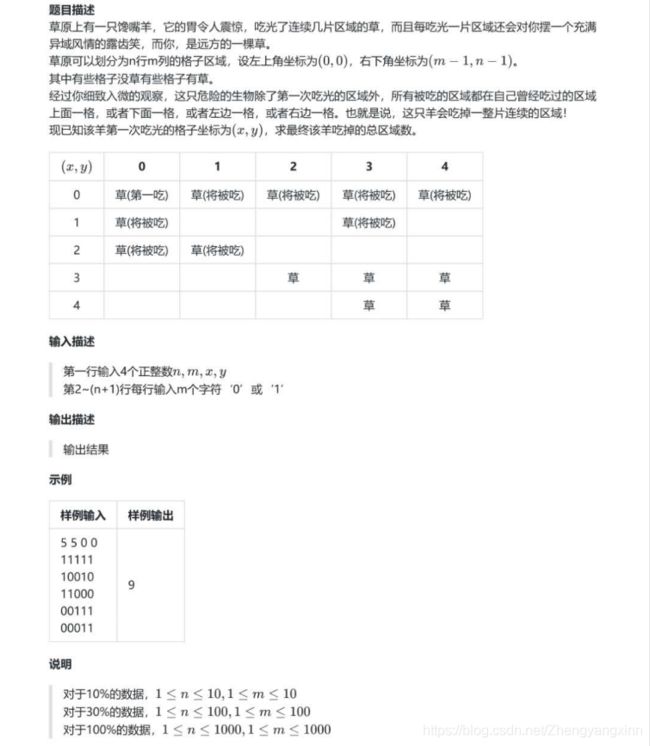
First question：馋嘴羊

BFS思路（可能会比较抽象，建议结合代码理解）：
第一步：输入矩阵、开始吃草位置
第二步：判断开始吃草位置1有没有草
如果有草
第三步：将该位置1入队
第四步：取队伍首元素为位置x
第五步：判断位置x上、下、左、右的位置有没有草
第六步：将有草的位置入队
第七步：将位置x对应的inf置为true,ans++
重复四~七步直到队伍中没有成员
最后输出ans
如果没草
输出0

#include
#include
using namespace std;
int n, m, x, y, ans=0;
const int maxn=1000;
int matrix[maxn][maxn];
bool inf[maxn][maxn]={false};

int X[4]={0, 0, -1, 1};
int Y[4]={-1, 1, 0, 0};

struct node{
	int x;
	int y;
}Node, top;

bool judge(int xx, int yy)
{
	if(xx<0||yy<0||xx>=n||yy>=m)
	return false;
	if(inf[xx][yy]==true||matrix[xx][yy]==0)
	return false;
	return true;
}


void BFS(int x, int y)
{
	queue<node> q;
	Node.x=x;
	Node.y=y;
	q.push(Node);
	while(!q.empty())
	{
		top=q.front();
		int nx=top.x;
		int ny=top.y;
		for(int i=0; i<4; i++)
		{
			if(judge(nx+X[i], ny+Y[i]))
			{
				Node.x=nx+X[i];
				Node.y=ny+Y[i];
				q.push(Node);
			}
		}
		ans++;
		inf[nx][ny]=true;
		q.pop();
	}
}


int main()
{
	cin>>n>>m>>x>>y;
	
	for(int i=0; i<n; i++)
	for(int j=0; j<m; j++)
	cin>>matrix[i][j];
	
	if(matrix[x][y]==1)
		BFS(x, y);
	cout<<ans;
	
	return 0;
}

Second question：走出迷宫

给定一个nm大小的迷宫，其中 * 代表不可通过的墙壁，而"."代表平地，S代表起点，T代表终点。移动过程中，如果当前位置是(x,y)(下标从0开始)，且每次只能前往上下左右(x,y+1),(x,y-1),(x-1,y)(x+1,y)四个位置的平地，求从起点S达到终点T的最少步数。

Sample Input:
5 5 //5行5列
… //迷宫信息
...
.S.
.**T
…
2 2 3 4 //起点S的坐标和终点T的坐标

Sample Output:
7
上面样例中，S的坐标为(2,2) T的坐标为(4,3)
注意：这道题与前面又略有不同，题目要求最少步数。
我们可以通过改变结点node结构，加入setp变量，作为记录每个位置的最少步数，这也体现了结构的灵活性。

#include
#include
using namespace std;

struct node{
	int x;
	int y;
	int step;
}Node, top;

const int maxn=1000;
char matrix[maxn][maxn];
bool inf[maxn][maxn]={false};
int X[4]={0,0,-1,1};
int Y[4]={-1,1,0,0};
int n, m, ant;
node a, S, T;

bool judge(int xx, int yy)
{
	if(xx<0||xx>=n||yy<0||yy>=m)
	return false;
	if(matrix[xx][yy]=='*'||inf[xx][yy]==true)
	return false;
	return true;
}

node BFS(int x, int y)
{
	queue<node> q;
	Node.x=x;
	Node.y=y;
	q.push(Node);
	while(!q.empty())
	{
		top=q.front();
		int nx=top.x;
		int ny=top.y;
		if(top.x==T.x&&top.y==T.y)//T.step只会被赋值一次，最先赋值路程最短 
		return top;
		for(int i=0; i<4; i++)
		{
			if(judge(nx+X[i], ny+Y[i]))
			{
				Node.x=nx+X[i];
				Node.y=ny+Y[i];
				Node.step=top.step+1;
				q.push(Node);
			}
		}
		inf[nx][ny]=true;
		q.pop();
	}
}


int main()
{
	cin>>n>>m;
	for(int i=0; i<n; i++)
	{
		getchar();
		for(int j=0; j<m; j++)
			matrix[i][j]=getchar();
	}
	cin>>S.x>>S.y>>T.x>>T.y;
	S.step=T.step=0;
	
	a=BFS(S.x, S.y);
	
	cout<<a.step<<endl;
	return 0;
}

Third question：01迷宫

有一个仅由数字0与1组成的n×n格迷宫。若你位于一格0上，那么你可以移动到相邻4格中的某一格1上，同样若你位于一格1上，那么你可以移动到相邻44格中的某一格0上。
你的任务是：对于给定的迷宫，询问从某一格开始能移动到多少个格子（包含自身）。

输入格式
第11行为两个正整数n,m。
下面n行，每行n个字符，字符只可能是0或者1，字符之间没有空格。
接下来m行，每行2个用空格分隔的正整数i,j，对应了迷宫中第i行第j列的一个格子，询问从这一格开始能移动到多少格。

输出格式
m行，对于每个询问输出相应答案。

输入输出样例
输入
2 2
01
10
1 1
2 2
输出
4
4
01迷宫 洛谷
注意：该题是查询某一块符合条件的个数，而且是多组输入。
若用到单纯BFS的思路的话，很容易造成重复查询的情况，导致超时。
为了避免超时，这里应当用BFS+记忆化剪枝的方式提高效率。

#include
using namespace std;
int mg[1010][1010], n, m;

//防止重复记格 
bool flag[1010][1010]={false};

int X[4]={0, 0, -1, 1};
int Y[4]={-1, 1, 0, 0};

struct node{
	int a;
	int b;
}Node, top;

bool judge(int xi, int yi, int x, int y)
{
	if(x<=0||y<=0||x>n||y>n)
	return false;
	if((mg[xi][yi]==1&&mg[x][y]==0)||(mg[xi][yi]==0&&mg[x][y]==1))
	return true;	
	return false;
}

map<int, int> mm;

int main()
{
	char ch;
	cin>>n>>m;
	
	for(int i=1; i<=n; i++)
	for(int j=1; j<=n; j++)
	{
		cin>>ch;
		if(ch=='0')
		mg[i][j]=0;
		else
		mg[i][j]=1;
	}
	
	while(m--)
	{
		int x, y, sum=0;
		cin>>x>>y;
		if(mg[x][y]==0||mg[x][y]==1)
		{
			queue<node> q;
			Node.a=x;
			Node.b=y;
			q.push(Node);
			while(!q.empty())
			{
				top=q.front();
//				cout<
				int xi=top.a;
				int yi=top.b;
				for(int i=0; i<4; i++)
				{
					if(judge(xi, yi, xi+X[i], yi+Y[i]))
					{
						Node.a=xi+X[i];
						Node.b=yi+Y[i];
						q.push(Node);
					}
				}
			//	防止重复记格 
				if(flag[xi][yi]==false)
					sum++;
				flag[xi][yi]=true;
				mg[xi][yi]=m+100010;
				q.pop();
			}
			mm[m+100010]=sum;
		}
/*		for(int i=1; i<=n; i++)
		{
			for(int j=1; j<=n; j++)
			cout<
		cout<<mm[mg[x][y]];
		if(m!=0) cout<<endl;
	}
	
	return 0;
} 

希望能够将自己的一些学习经验分享给有需要的人。
我是小郑，一个坚持不懈的小白。
参考博客