字符串科技:Palindrome Series
文章目录
- 简介
- 背景知识
- 弱周期定理
- Border Series
- Palindrome Series
- PAM
- 例题:CF 932G
- 题意
- 题解
- 暴力DP
- 使用Palindrome Series优化DP
- 符号约定
- 转移方法
- 总结
- 代码
- 第二个题: 2019 ICPC 沈阳 M
- Note
- 题意
- 题解
- 代码
- 强行第三个题:CF 17E
- 题意
- 题解
- 代码
- 总结
简介
其实不太清楚这个应该叫什么,知道的同学可以麻烦告知我。
众所周知,一个串的border数量是 O ( n ) O(n) O(n)的,但是他们可以用 O ( l o g n ) O(logn) O(logn)段等差数列表示。
这个东西叫做Border Series,然后把他和回文串结合起来放在PAM上使用,就是本文说的Palindrome Series了。
这东西代码实际非常短,使用的时候,只需要修改3行(DP转移部分)。
背景知识
弱周期定理
这里不详细展开讲,这是一个well known的定理,在使用Series相关的科技时会反复用到,可以自行搜索了解。
Border Series
一个串的长度在 [ 2 k , 2 k + 1 ) [2^k,2^{k+1}) [2k,2k+1)范围内的border长度构成等差数列,证明使用上面的弱周期定理,可以参考2019国集论文等很多资料,不讲。
Palindrome Series
考虑一个回文串 S S S的后缀 T T T,则有: T T T是回文串与 T T T是 S S S的border 等价。再结合上面的Border Series,即可得到一个推论:一个回文串的所有回文后缀可以表示为 O ( l o g n ) O(logn) O(logn)段等差数列。设法对每段等差数列进行维护,就可以 O ( l o g n ) O(logn) O(logn)枚举所有回文后缀,这就是Palindrome Series做的事情。
PAM
前置技能点:Palindrome Automaton,回文自动机。
例题:CF 932G
题意
转化之后的题意为:给一个串 S ( ∣ S ∣ ≤ 1 0 6 ) S(|S| \le 10^6) S(∣S∣≤106),规定一个 S S S的分割是合法的当且仅当:分割的每一部分都是偶回文串。
求合法的分割方案数。
题解
暴力DP
很容易直接想到暴力DP的办法:设 f [ i ] f[i] f[i]表示将串 S [ 1 , i ] S[1,i] S[1,i]进行分割的方案数。
初始化 f [ 0 ] = 0 f[0] = 0 f[0]=0,转移为
f [ i ] = ∑ 1 ≤ j < i f [ j ] ⋅ [ S [ j + 1 , i ] 是 偶 回 文 串 ] f[i] = \sum_{1 \le j < i} f[j] \cdot [S[j+1,i]是偶回文串] f[i]=1≤j<i∑f[j]⋅[S[j+1,i]是偶回文串]
也就是我们需要枚举所有 S [ 1 , i ] S[1,i] S[1,i]的(偶)回文后缀。使用PAM,全 a a a串的复杂度为 O ( n 2 ) O(n^2) O(n2),不能通过。
使用Palindrome Series优化DP
符号约定
l e n [ i ] len[i] len[i] 表示节点代表的回文串长度
f a i l [ i ] fail[i] fail[i] 表示节点的失配指针,即最长的回文后缀,即最大border。
d i f f [ i ] = l e n [ i ] − l e n [ f a i l [ i ] ] diff[i] = len[i] - len[fail[i]] diff[i]=len[i]−len[fail[i]] ,表示一个节点和他最大border长度的差,即所在的等差数列的公差。
a n c [ i ] anc[i] anc[i] 表示节点所在等差数列的首项位置,即从 i i i开始往根走,保证 d i f f diff diff值都相同,最终走到的点。
g [ i ] g[i] g[i] 维护每个点到链顶的信息,维护的范围是 ( l e n [ a n c [ i ] ] , l e n [ i ] ] (len[anc[i]],len[i]] (len[anc[i]],len[i]],公差 d = d i f f [ i ] d = diff[i] d=diff[i]。
f [ i ] f[i] f[i] 表示 D P DP DP值,即将串 S [ 1 , i ] S[1,i] S[1,i]进行分割的方案数。
转移方法
l e n , f a i l , d i f f , a n c len,fail,diff,anc len,fail,diff,anc都可以在构造 P A M PAM PAM的过程中求得。
重点在于 f , g f,g f,g的相互转移。
根据定义: f [ i ] = ∑ p g [ p ] f[i] = \sum_{p} g[p] f[i]=∑pg[p],其中 p p p是在PAM上跳到的点,跳的方式是每次从 p p p跳到 a n c [ p ] anc[p] anc[p],即每次 O ( 1 ) O(1) O(1)求得一段等差数列的信息,然后跳到下一个等差数列。
g g g的转移是动态的,或者理解成是离线的。大概需要理解下面这个事情:
设我们现在 S = a b a b a b a b a S = ababababa S=ababababa,现在在 i = 7 i=7 i=7进行转移。即 g [ p ] = f [ 0 ] + f [ 2 ] + f [ 4 ] + f [ 6 ] g[p] = f[0] + f[2] + f[4] + f[6] g[p]=f[0]+f[2]+f[4]+f[6]

我们观察当 p ′ = f a i l [ p ] p' = fail[p] p′=fail[p]的时候 g g g的情况:有 g [ p ′ ] = f [ 0 ] + f [ 2 ] + f [ 4 ] g[p'] = f[0] + f[2] + f[4] g[p′]=f[0]+f[2]+f[4]
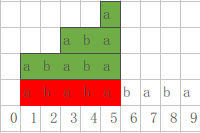
我们发现了一件事情: g [ p ] g[p] g[p]只比 g [ p ′ ] g[p'] g[p′]多维护了一个信息 f [ 6 ] f[6] f[6],即属于该等差数列最短的回文串代表的信息。
这个事情的原因是因为Border Series,观察到这一段后缀的公差是 d = 2 d = 2 d=2,于是每个在 i = 7 i=7 i=7位置的border,将长度 − d -d −d,就会成为一个在 i = 5 i=5 i=5处的border,也就是将 i = 7 i=7 i=7的border直接砍掉后边两个字符,就变成 i = 5 i=5 i=5的border。
因此只有在 i = 7 i=7 i=7位置新出现的一个最短的border的信息,是需要额外维护的。而他的长度为 l e n [ a n c [ i ] ] + d i f f [ i ] len[anc[i]] + diff[i] len[anc[i]]+diff[i],只需要将这1个信息简单的合并即可(加起来)。
总结
g g g数组的转移是动态的,之前的值不会影响到现在的值。在某个位置 p p p转移的时候, f a i l [ p ] fail[p] fail[p]一定是有意义的,在上面的例子中表现为:在 i = 7 i=7 i=7处转移的时候, p ′ = f a i l [ p ] p'=fail[p] p′=fail[p]是 i = 5 i=5 i=5位置,其对应的 g [ p ′ ] g[p'] g[p′]是有意义的。
一句话说就是:在转移的过程中,整个PAM上只有当前点 p p p到跟的链上的信息是有意义的,这是由串的Lyndon结构所决定的。
代码
DP转移部分:
void trans(int i){
for (int p = last;p>1;p = anc[p]){
g[p] = f[i - l[anc[p]] - diff[p]];
if (diff[p] == diff[fail[p]]){
(g[p] += g[fail[p]]) %= mod;
}
(f[i] += (i % 2 == 0) *g[p]) %= mod;
}
}
完整代码:
// Created by calabash_boy on 19-11-20.
// CF 932G
// 偶回文分割方案数
#include第二个题: 2019 ICPC 沈阳 M
Note
现场赛由于出题人不学无术,本题标程(正确性错误)和数据(极其弱)都是假的,而现场的50多个AC只有一个是正解(比较符合这题的难度预期?),其他都是暴力或者假贪心。
std是错的,但是数据都是对的,可能这就是神仙吧。
题意
给出串 S S S,要求在 S S S 中选出3个互不相交的回文子串,求长度之和的最大值。
题解
再喷一波出题人,字符串题不是计数,而是敢出最优化问题,我只想说:您配吗?
好了,说这个题正确的做法,依然是一个很简单的 D P DP DP,设 f [ i ] [ k ] f[i][k] f[i][k]为在 S [ 1 , i ] S[1,i] S[1,i]中选出了 k k k个不相交回文子串,其长度和的最大值。
转移也很简单:
i i i位置不选:
d p [ i ] [ k ] = d p [ i − 1 ] [ k ] dp[i][k] = dp[i-1][k] dp[i][k]=dp[i−1][k]
k = 1 k = 1 k=1时:
f [ i ] [ 1 ] = l e n [ p ] , 其 中 p 是 串 S [ 1 , i ] 在 P A M 上 对 应 的 点 f[i][1] = len[p],其中p是串S[1,i]在PAM上对应的点 f[i][1]=len[p],其中p是串S[1,i]在PAM上对应的点
2 ≤ k ≤ 3 2 \le k \le 3 2≤k≤3时,枚举回文后缀:
f [ i ] [ k ] = max 1 ≤ j < i ( f [ j ] [ k − 1 ] + i − j ) = max 1 ≤ j < i ( f [ j ] [ k − 1 ] − j ) + i f[i][k] = \max_{1\le j < i}{(f[j][k-1] + i - j)} = \max_{1\le j < i}(f[j][k-1] - j) + i f[i][k]=1≤j<imax(f[j][k−1]+i−j)=1≤j<imax(f[j][k−1]−j)+i
与上一个题没有区别,只是把 ∑ \sum ∑变成了 m a x max max以及维护的东西变成了 f [ j ] [ k ] − j f[j][k] - j f[j][k]−j而已,直接套用相同的做法即可。
代码
DP转移部分:
void trans(int i){
for (int k=0;k<3;k++){
f[i][k] = f[i-1][k];
for (int p = last;p>1;p = anc[p]){
g[p][k] = f[i - l[anc[p]] - diff[p]][k] - (i - l[anc[p]] - diff[p]);
if (diff[p] == diff[fail[p]]){
g[p][k] = max(g[p][k], g[fail[p]][k]);
}
f[i][k] = max(f[i][k],k == 0?l[p] :( g[p][k-1] + i));
}
}
}
完整代码:
// Created by calabash_boy on 19-11-20.
#include强行第三个题:CF 17E
题意
给出一个串S,找到所有回文子串,统计有多少个pair他们的区间是相交的。
现在加强一下好了,要求对于 S S S的每个前缀在线的输出答案。
题解
不加强的可以直接离线,马拉车然后跑两遍就做完了。
而我们的算法是在线的,因为PAM构造就是在线的。
首先容斥一下,我们求不相交的。
设
d e p [ p ] dep[p] dep[p]为一个点在PAM上的深度,也就是某个串的回文后缀数量。
F [ i ] F[i] F[i] 为 S [ 1 , i ] S[1,i] S[1,i]的回文子串数量。显然 F [ i ] = F [ i − 1 ] + d e p [ p ] F[i] = F[i-1] + dep[p] F[i]=F[i−1]+dep[p]。
f [ i ] f[i] f[i]为以 i i i结尾的回文串对答案的贡献。即固定一个串必须以 i i i结尾,有多少个不相交pair。显然 f [ i ] = ∑ j F [ j ] f[i] = \sum_{j}F[j] f[i]=∑jF[j],其中 S [ j + 1 , i ] S[j+1,i] S[j+1,i]为回文串,即转移的形式依然是:枚举所有回文后缀。
所以直接把 F F F放在Palindrome Series上维护和,就可以解决这个题。。。唯一问题在于这个题他比较远古,PAM会卡内存,要把 n x t nxt nxt数组变成前向星才够。
代码
转移部分:
void trans(int i){
F[i] = (F[i-1] + dep[last]) % mod;
for (int p = last;p>1;p = anc[p]){
g[p] = F[i - l[anc[p]] - diff[p]];
if (diff[p] == diff[fail[p]]){
(g[p] += g[fail[p]]) %= mod;
}
(f[i] += g[p]) %= mod;
}
}
完整代码:
// Created by calabash_boy on 19-11-20.
#include总结
Palindrome Series科技使用的情况为:枚举所有的回文后缀,这时直接套用该科技就可以把一个 n n n变成一个 l o g n logn logn,常数极小。
由于PAM是增量构造法,且构造时没有 S A M SAM SAM那样的节点分裂,于是 f , g f,g f,g数组都可以直接在构造的时候一起计算,代码可以非常短,比如我的代码只需要修改3行。